目录

一.数据结构(树)

二.二叉树(任意节点的度<=2)

二叉查找树又称为二叉排序树/二叉搜索树

平衡二叉树

平衡二叉树的旋转机制

三.红黑树

---

一.数据结构(树)

基本概念:

度: 每一个节点的子节点数量

树高: 树的总层数

根节点: 最顶层的节点

左子节点: 左下方的节点

右子节点: 右下方的节点

根子节点的左子树:看图

 根子节点的右子树:看图

 

二.二叉树(任意节点的度<=2)

二叉查找树又称为二叉排序树/二叉搜索树

特点:

(1)每个节点上最多有两个子节点

(2)任意节点左子树上的值都小于当前节点

(3)任意节点右子树上的值都大于当前节点

添加节点的规则:

小的存左边, 大的存右边, 一样的不存

遍历方式:

(1)前序遍历: 当前节点, 左子节点, 右子节点

(2)中序遍历: 左子节点, 当前节点, 右子节点

(3)后序遍历: 左子节点, 右子节点, 当前节点

(4)层序遍历: 一层一层的去遍历

平衡二叉树

规则: 任意节点左右子树高度差不超过1

平衡二叉树的旋转机制

规则1: 左旋

规则2: 右旋

触发时机: 当添加一个节点之后,该数不再是一颗平衡二叉树

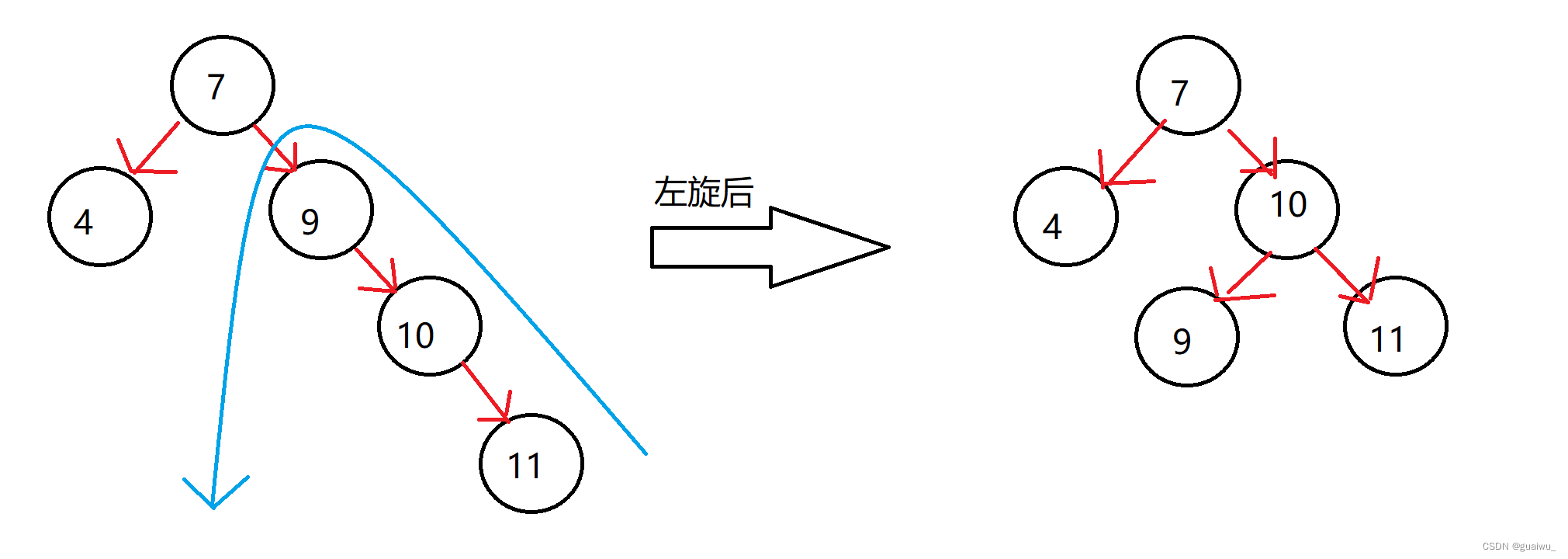
比较简单的左旋

步骤:(1)以不平衡的点作为支点(从添加点开始,不断往父类找不平衡的点)

(2)把节点左旋降级,变成左子节点

(3)晋升原来的右子节点

有点难的左旋

步骤:(1)以不平衡的点作为支点

(2)将根节点的右侧往左拉

(3)原先的右子节点变成新的符节点,并把多余的左节点出让,给已经降级的根节点当右子节点

 右旋的话也差不多 

左左: 当根节点左子树的左子树有节点插入,导致二叉树不平衡      (一次右旋解决)

左右: 当根节点左子树的右子树有节点插入,导致二叉树不平衡      (先局部左旋,再整体右旋)

右右: 当根节点右子树的右子树有节点插入,导致二叉树不平衡      (一次左旋解决)

右左: 当根节点右子树的左子树有节点插入,导致二叉树不平衡      (先局部右旋,再整体左旋)

三.红黑树

是二叉查找树: 满足小的在左边, 大的在右边

但高度不是平衡的

条件:特有的红黑规则

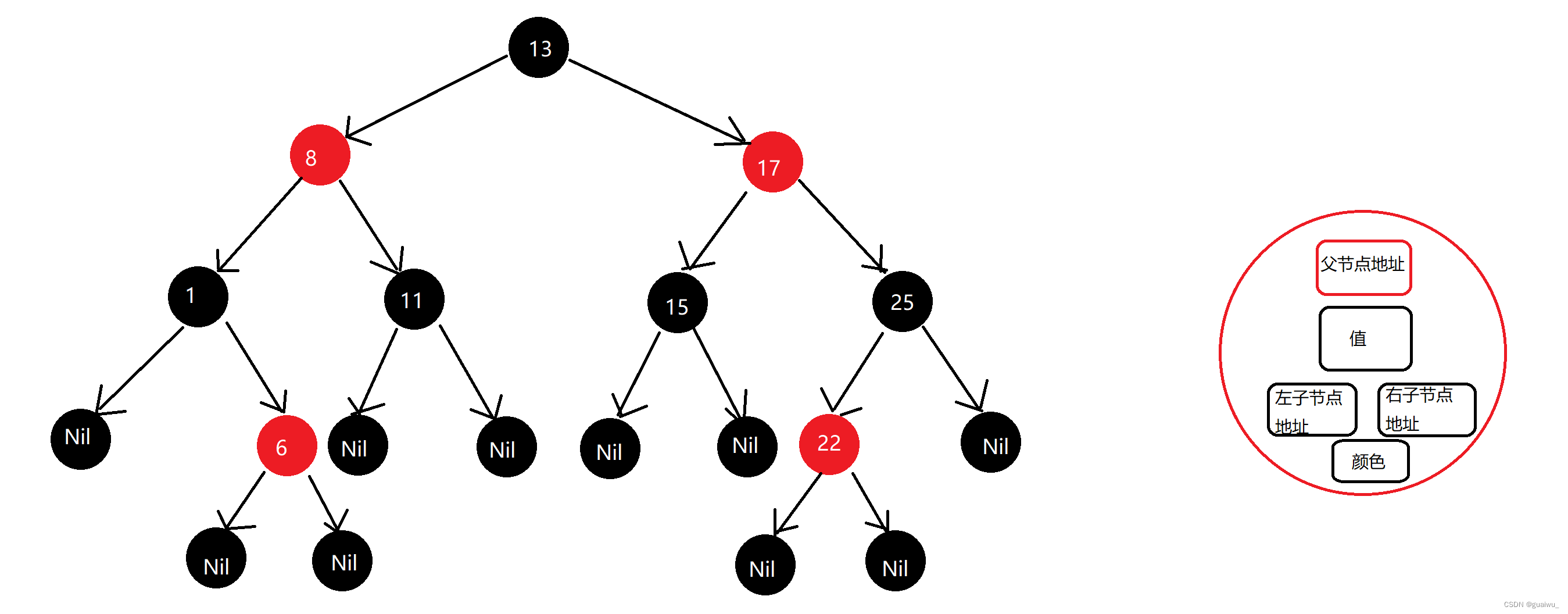
红黑规则:

(1)每一个节点或是红色的,或者是黑色的

(2)根节点必须是黑色

(3)如果一个节点没有子节点或者父节点,则该节点想要的指针属性值为Nil,这些Nil为叶节点, 每个叶节点(Nil)是黑色的

(4)如果某一个节点是红色, 那么它的子节点必须是黑色(不能出现两个红色节点相连)

(5)对每一个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点