( “树” 之 DFS) 572. 另一棵树的子树 —

( “树” 之 DFS) 572. 另一棵树的子树 ——【Leetcode每日一题】

news2024/9/29 9:23:21

572. 另一棵树的子树

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

示例 1：

在这里插入图片描述

输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true

示例 2：

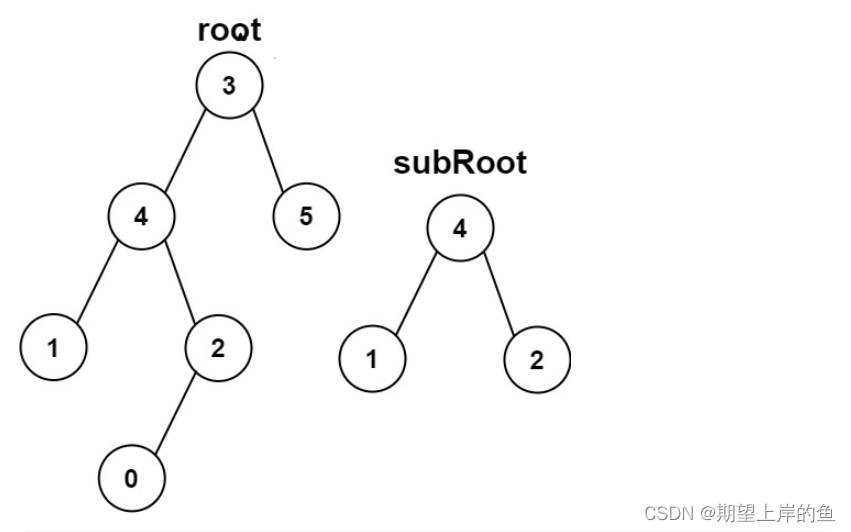
在这里插入图片描述

输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出：false

提示：

root 树上的节点数量范围是 [1, 2000]
subRoot 树上的节点数量范围是 [1, 1000]
$10^4 <= root.val <= 10^4$
$10^4 <= subRoot.val <= 10^4$

思路：DFS

首先任意看一个节点的root.val，该节点可能等于subRoot.val，也可能不相等，共有两种可能，对应的也就有两种不同的操作：

当root.val == subRoot.val时，则判断剩余的后代节点是否都相等，如果有其中一个不相等，则subRoot不是root的子树，返回false，如果走到叶子节点都相等的话返回true;
当root.val != subRoot.val时, 则接着到root的左右节点比较，只要有其中一个满足子树，就返回true;
递归上述两种情况则可判断是否存在子树。

代码：(Java、C++)

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(root == null || subRoot == null) {
            return false; 
        }
        return dfs(root, subRoot) || isSubtree(root.left, subRoot) || isSubtree(root.right, subRoot);
    }
    public boolean dfs(TreeNode root, TreeNode subRoot) {
        if(root == null && subRoot == null) return true;
        if(root == null || subRoot == null || root.val != subRoot.val){
            return false;
        } 
        return dfs(root.left, subRoot.left) && dfs(root.right, subRoot.right);
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if(root == NULL || subRoot == NULL) {
            return false; 
        }
        return dfs(root, subRoot) || isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
    }
    bool dfs(TreeNode* root, TreeNode* subRoot) {
        if(root == NULL && subRoot == NULL) return true;
        if(root == NULL || subRoot == NULL || root->val != subRoot->val){
            return false;
        } 
        return dfs(root->left, subRoot->left) && dfs(root->right, subRoot->right);
    }
};

运行结果：

在这里插入图片描述

复杂度分析：

时间复杂度： $O (n * m)$ ，m为root的节点数，n为subRoot的节点数，对于每一个root上的点，都需要做一次深度优先搜索来和subRoot匹配，匹配一次的时间代价是 $O (m)$ 。
空间复杂度： $O (n)$ ，考虑到递归需要在栈上开辟空间，最大深度为n。