单链表
链表优点:
1.按需申请空间,需要就申请,不需要就释放
2.头部或中间插入数据,不需要挪动数据
3.不存在空间浪费
缺点:
1.每次存放一个数据,到要存一个指针去链接后面的数据节点
2.不支持随机访问(用下标直接访问某i个)
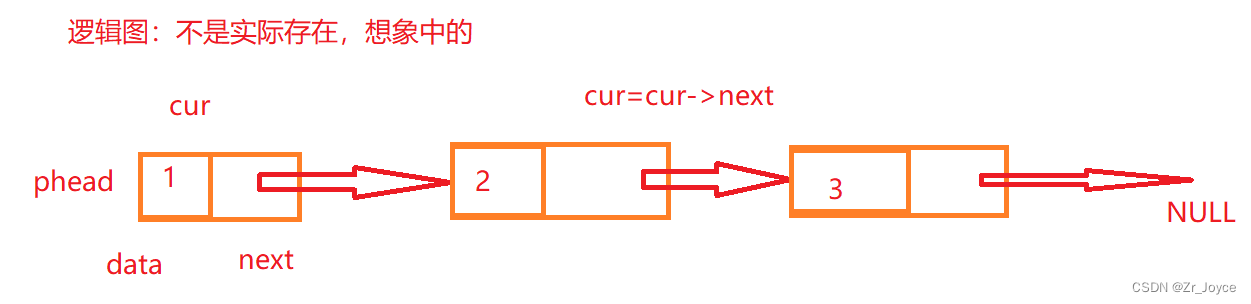

*cur->next指向下一个数据,然后cur->data指向下一个数据的数值
该示例中结构体 存储1个数值+下一个节点的地址
当下一个节点的地址为空,则结束*
尾插数据 :
123节点后插入一个新节点4,4后指向空指针
void SLtPushBack(SLT* phead, SLTDataType x)
{
// 找尾节点
SLT* tail = phead;
while (tail->next != NULL)
{
tail = tail->next;
}
SLT* newcode = (SLT*)malloc(sizeof(SLT));
newcode->data = x;
newcode->next = NULL;
tail->next = newcode;
}ps: malloc里sizeof后应为SLT,是整个结构体类型大小
如果这样写代码,则会 报错
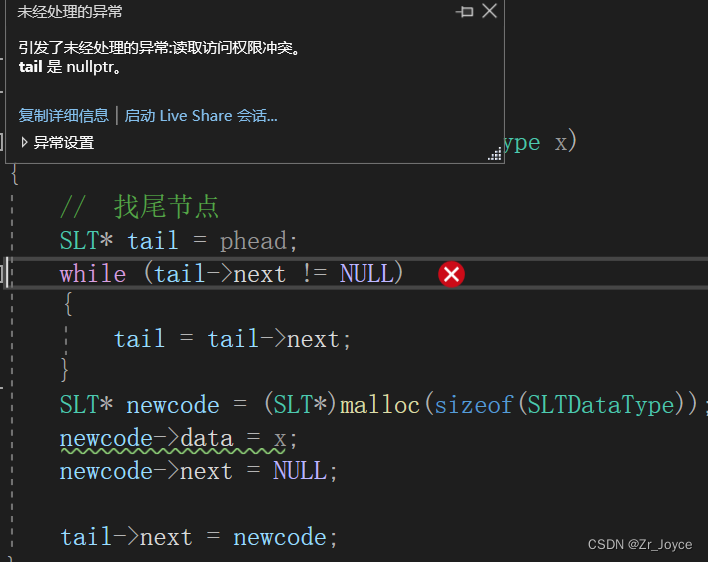
因为 tail 本就是NULL空,-> 操作是解引用,对空的tail解引用非法访问
如果这么写:
void SLtPushBack(SLT* phead, SLTDataType x)
{
// 找尾节点
SLT* newcode = (SLT*)malloc(sizeof(SLT));
newcode->data = x;
newcode->next = NULL;
if(phead==NULL)
{
phead=newnode;
}
else
{
SLT* tail = phead;
while (tail->next != NULL)
{
tail = tail->next;
}
tail->next = newcode;
}
}改变了形参phead,未改变实参plist
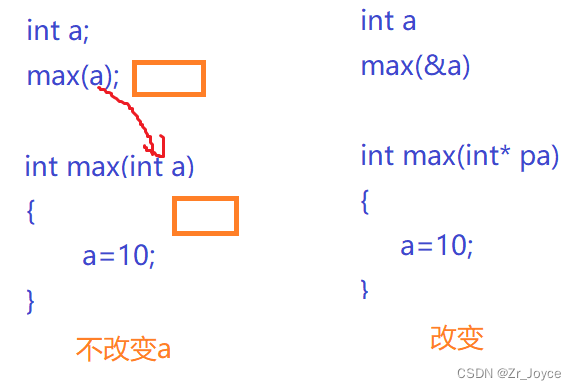
实参是int,要改变a,要传int*,解引用找到a改变
实参是int*,要传int**,解引用找到int
同理:
void SLtPushBack(SLT** pphead, SLTDataType x)
{
// 找尾节点
SLT* newnode = (SLT*)malloc(sizeof(SLT));
newnode->data = x;
newnode->next = NULL;
if (*pphead == NULL)
{
*pphead = newnode; // 解引用
}
else
{
SLT* tail = *pphead;
while (tail->next != NULL)
{
tail = tail->next;
}
tail->next = newnode;
}
}①创建节点
SLT* CreatListNode(SLTDataType x)
{
SLT* newnode = (SLT*)malloc(sizeof(SLT));
newnode->data = x;
newnode->next = NULL;
return newnode;
}②尾插:
void SLtPushBack(SLT** pphead, SLTDataType x)
{
// 找尾节点
/*SLT* newnode = (SLT*)malloc(sizeof(SLT));
newnode->data = x;
newnode->next = NULL; */ // 直接封装成一个函数,如上
SLT* newnode = CreatListNode(x);
if (*pphead == NULL)
{
*pphead = newnode; // 解引用
}
else
{
SLT* tail = *pphead;
while (tail->next != NULL)
{
tail = tail->next;
}
tail->next = newnode;
}
}③头插
void SLtPushFront(SLT** pphead, SLTDataType x)
{
SLT* newnode = CreatListNode(x); // 创建新节点,值x已经传入newnode
newnode->next = *pphead; // 将原来头的地址放入新节点的next
*pphead = newnode; // 将新节点作为新的头
}