时间序列信号阈值降噪方法，有什么可以创新的地方吗?

news2024/11/27 8:30:38

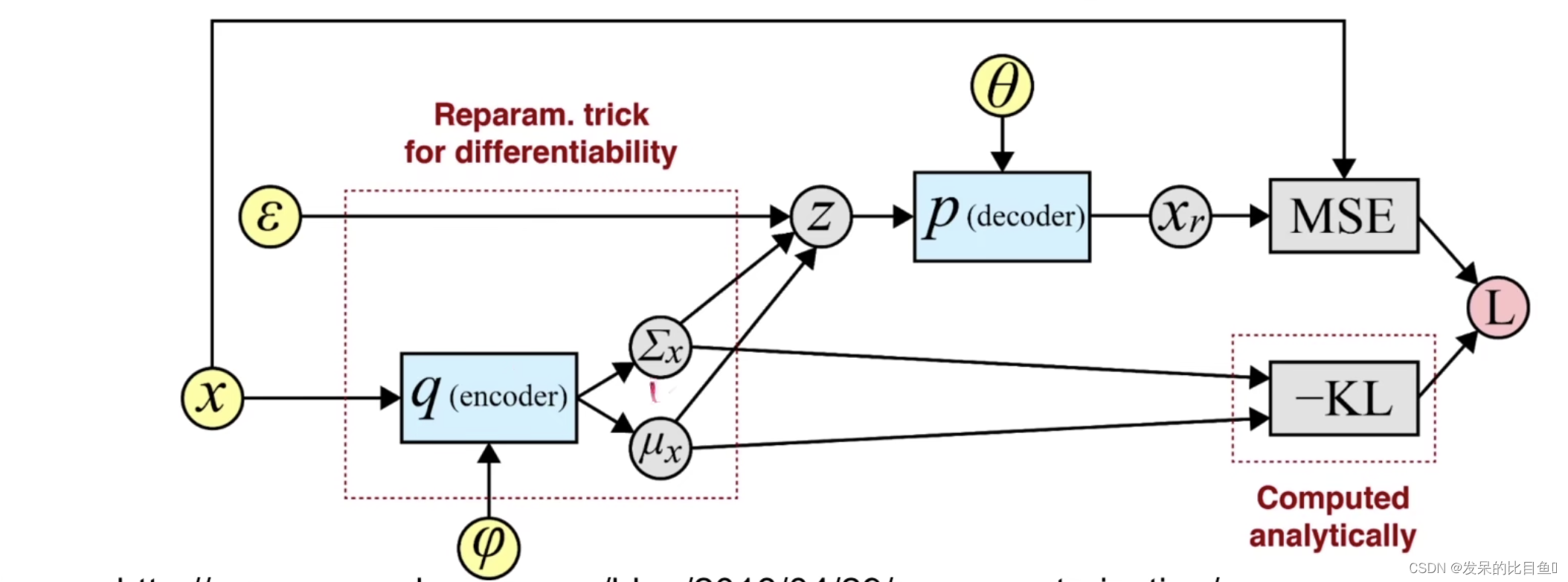
可以换个空间，从图域的角度进行分析，比如图傅里叶变换，图小波变换等图时频分析方法。图小波阈值降噪的基本思想是通过将时间序列信号转换成路图信号，再利用图小波变换分解成尺度函数系数和一系列对应不同尺度的谱图小波系数，然后设置阈值对图小波系数进行过滤处理，最后对尺度函数系数和滤波后的图小波系数进行图小波逆变换，重构得到降噪信号。

更具体地，图小波变换将路图信号分解成低频分量和高频分量，其中尺度函数系数包含信号的低频近似成分，图小波系数反映信号的高频细节成分。各尺度上的图小波系数在某些特定位置的幅值较大，对应于原始信号的奇变位置和重要信息，而其他大部分位置的幅值较小，对应于噪声干扰成分。噪声对应的图小波系数在每个尺度上的分布较均匀，且幅值随着尺度的减小而逐渐减小。因此，通常的降噪方法是设置一个合适的临界阈值ρ，并结合阈值函数对系数进行滤波。当图小波系数小于阈值ρ时，认为此系数主要由噪声引起，则将其置为零进行消除；当图小波系数大于或等于阈值ρ时，认为此系数主要由信号引起，则予以保留或进行收缩，从而得到估计谱图小波系数。最后，对所有剩余系数进行重构即可获得降噪信号。

此外：从图的角度分析一维信号有什么优势？

传统方法只从信号离散点中提取特征信息，忽略了离散点间关系所包含的信息。通过在图上定义信号，则可将信号从一般数据域转换到图域，从而利用图来反映原始信号的局部性关系。在图域中，信号的数据结构可以提供额外的输入信息，不仅包括对应于图中顶点的信号离散点函数值，还包括顶点间的关系。这个关系主要表现为顶点间的相似度，通过边权重来反映。因此，从图的角度分析一维信号不仅可以挖掘信号离散点所包含的信息，还分析了离散点间的相似度信息。

对于机械振动信号，权重反映的相似度信息可以描述相邻时刻间振动加速度的变化趋势，较大的权重表示加速度变化较大，较小的权重表示加速度变化较小。在图域中对其进行处理时，可同时分析振动加速度的瞬时大小和振动加速度的局部变化趋势，从而极大地丰富了分析过程中的输入信息，进而有效提高特征描述的准确性。