常用算法

时间复杂度

在日常生活中, 我们描述物体的重量使用的是kg, 描述物体的长度使用的是m, 那么相对的, 在计算机科学中也需要一种度量来定性地描述算法的运行时间, 这种度量方法称为大O表示法.

• 声明f(n)作为我们的函数, n表示的参数. 不同的参数会导致算法运行的时间不同. 那么最坏的情况就是T(n)

• T(n) = O(f(n)), f(n)表示表达式执行的次数之和.

  def foo(n):
  	for i in range(n):
  		表达式
  f(n) = n
  T(n) = O(n)
  该算法的时间复杂度为O(n)
  

  • 键对值取值

    O(1)
    

  • 嵌套的for循环

    for i in range(n):
    	for j in range(m):
    		表达式
    
    O(n*m)
    

  • 执行多次的for循环

    for i in range(n):
    	表达式
    for j in range(n):
    	表达式
    
    O(2n)
    

    上述代码时间复杂度为O(2n), 但是在大O表示法当中, 可以忽略系数和常数, 所以当前的时间复杂度也可以写为O(n)

  • 二分法

    2**3 = 8
    3 = log8
    f(n) = logn
    
    O(logn)
    

常见的排序

https://www.runoob.com/w3cnote/selection-sort.html

• 选择排序
• 冒泡排序
• 插入排序
• 归并排序
• 快速排序
• 桶排序

选择排序O(n²)

• 从当前元素后的无序元素数组中找到最小值

• 如果找到了, 将该元素与当前元素交换

• 如果没找到, 说明当前元素是后续无序数组中的最小值

• 执行上述过程n-1次

  def selection_sort(array):
      # 最后一个元素无序比较, 所以执行n-1次
      for i in range(len(array)-1):
          min_index = i
          # 从当前index+1的位置开始遍历
          for j in range(i+1, len(array)):
              if array[j] < array[min_index]:
                  min_index = j
  
          # 如果找到最小值
          if i != min_index:
              array[i], array[min_index] = array[min_index], array[i]
  

冒泡排序O(n²)

• 本质就是将最大值移动到数组末端

• 比较cur和next, 如果cur > next, 则交换两者

• 执行上述过程n次

  def bubble_sort(array):
      for i in range(len(array)):
          # 每完成一次遍历, 结尾就有一个最大元素, 那么我们接下来的遍历过程可以-1
          for j in range(len(array)-1-i):
              # array[j]表示cur
              if array[j] > array[j+1]:
                  array[j], array[j+1] = array[j+1], array[j]
  

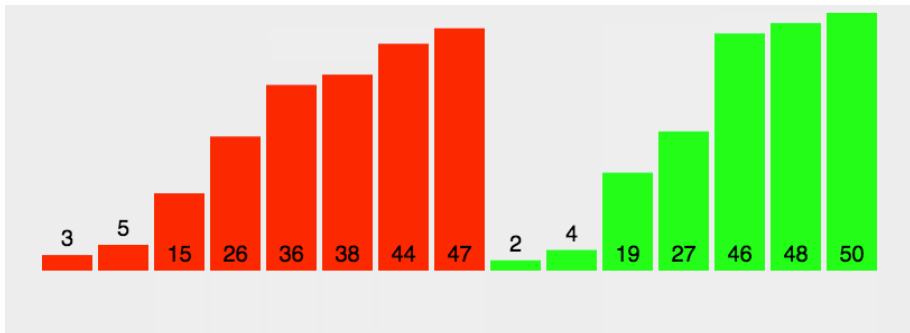
归并排序

归并排序适用于两个有序数组进行重新排序

• 合并两个有序数组

  • 声明一个新数组, 该数组的长度 = 左数组 + 右数组

  • 比较两个左数组和右数组的头元素, 小的值将添加到新数组的头部

  • 重复步骤2, 直到某个数组没有元素为止

  • 将剩余元素的数组直接添加到新数组末端

    def merge(left, right):
        """
        :param left:  左数组
        :param right: 右数组
        :return:
        """
        # 因为我们是python的list, 所以不用考虑声明长度
        result = []
        while left and right:
            # 比较两个数组的头元素
            if left[0] <= right[0]:
                # 通过list.pop删除并返回指定位置的元素
                result.append(left.pop(0))
            else:
                result.append(right.pop(0))
    
        while left:
            result.append(left.pop(0))
    
        while right:
            result.append(right.pop(0))
    
        return result
    

• 对无序的数组进行重新排序

  无序数组[a, b, c, d, e] 可以拆分成[a, b], [c, d, e]

  [a, b] 排序后得到[b, a]

  [c, d, e]可以拆分为[c, d], [e]

  [c, d] 排序后得到[d, c]

  得到了三组有序数组

  [d, c], [e] 归并后得到[d, c, e]

  [d, c, e], [b, a]归并后得到[d, b, c, a, e]

  def merge_sort(array):
      """
      使用递归实现分治思想
      :param array:
      :return:
      """
      # 一旦使用递归, 首先要考虑的是退出逻辑
      if len(array) < 2:
          return array
  
      middle = len(array) // 2
      left_array = array[:middle]
      right_array = array[middle:]
      return merge(merge_sort(left_array), merge_sort(right_array))
  

快速排序

• 从数组中选定一个基准(pivot)

• 遍历基础之后的元素, 将比它小的元素置于左边, 比它大的元素置于右边

  • 声明i, j两个指针
  • 比较pivot和j的值, 如果pivot > j, 交换i和j的值, i+1
  • 不管比较的结果, j + 1
  • j到达末端, pivot和i-1交换值

  def partition(array, left, right):
      """
      :param array:
      :param left: 左端索引
      :param right: 右端索引
      :return:
      """
      # 为了方便我们理解, 这里选left
      pivot = left
  
      i = j = pivot + 1
      while j <= right:
          if array[pivot] > array[j]:
              array[i], array[j] = array[j], array[i]
              i += 1
          j += 1
  
      array[i-1], array[pivot] = array[pivot], array[i-1]
      # 返回原pivot值的新索引
      return i-1
  

• 实现分治思想

  def quick_sort(array, left, right):
      if left < right:
          pivot = partition(array, left, right)
          # 子任务的排序不需要考虑pivot
          quick_sort(array, left, pivot-1)
          quick_sort(array, pivot+1, right)
  

动态规划

https://baike.baidu.com/item/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92/529408?fr=aladdin

动态规划（Dynamic Programming，DP）是运筹学的一个分支，是求解决策过程最优化的过程. 在多阶段决策问题中，各个阶段采取的决策，一般来说是与时间有关的，决策依赖于当前状态，又随即引起状态的转移，一个决策序列就是在变化的状态中产生出来的，故有“动态”的含义，称这种解决多阶段决策最优化的过程为动态规划方法.

简单地说, 动态规划的本质就是穷举所有的可能性, 寻找最优解.

• 动态规划的应用

  一切求最值得情况, 都可以通过动态规划来解决.

  • 资金管理问题
  • 资源分配问题
  • 最短路径问题
  • 最优决策问题

• 动态规划的思想

  • 通过分治法来实现动态规划决策的过程

    • 将待解决的问题分解成若干个子问题, 先求解子问题.

  • 动态规划会产生大量的重复计算.

  • 动态规划中当前状态取决于上一阶段状态和本阶段的状态

    • 基于2, 3两点. 所以动态规划使用的是数组来做为缓存数据结构, 而不是hashmap, 该数组被称位dp_table(dynamic programming table)

• 动态规划的解题步骤

  • 列出状态转移方程

    # 暂时简单地理解为可以用来表达任意子问题的方程式
    dp_table[n] = f(dp_table[n-1])
    

  • 初始化长度为n的dp_table

    • 分治思想最终会达到拆无可拆的地步, 该情形下就是dp_table的初始值

      在斐波那契函数当中, 索引值小于2就是拆无可拆的地步

  • 穷举所有决策和记录产生的结果/状态

    • dp_table最终会被填满, 即所有的可能性已经穷举完毕
    • 一般来说, dp_table[-1]就是我们要求的最值

题集

• 斐波那契函数

  斐波那契函数严格来说不属于动态规划, 因为它不必求最值. 这里我们只用它体现将问题变成求解子问题的过程

  def fib(n):
      """
      斐波那契函数当前值等于前两个值之和
      0, 1, 1, 2, 3, 5
  
      1. 写出状态转移方程 fib(n) = fib(n-1) + fib(n-2)
      2. 考虑最终子问题的初始值
      :param n:
      :return:
      """
      if n < 2:
          return n
  
      return fib(n-1) + fib(n-2)
  

• 爬楼梯

  def upstairs(n):
      """
      台阶1: [1]
      台阶2: [1 + 1], [0 + 2]
      台阶3: ([1 + 1 + 1], [0 + 2 + 1]), ([1 + 2])
      台阶4: ([1 + 1 + 1 + 1], [0 + 2 + 1 + 1], [1 + 2 + 1]), ([1 + 1 + 2], [0 + 2 + 2])
  
      dp_table[n] = dp_table[n-1] + dp_table[n-2]
      :param n:
      :return:
      """
      dp_table = [0] * n
  
      # 初始化dp_table
      dp_table[0], dp_table[1] = 1, 2
  
      # 填满dp_table, 遍历n即可
      for i in range(2, n):
          dp_table[i] = dp_table[i-1] + dp_table[i-2]
  
      return dp_table[-1]
  
  

• 买股票的最佳时机1

  def max_profit(prices):
      """
      - 只有两次操作, 一次为买, 一次为卖
      - 最大利润 = 最高位 - 最低位
  
      股票问题的难点在于要考虑所谓的状态不仅仅表示上一个状态的值(也就是利润的最大值)
      还要考虑股票的状态, 因为股票买了之后持有是有价值的, 但是暂时不能算作利润.
      最终利润 = 持有的股票 - 当前股价. 也点出了股票的本质就是未来的期望
                      卖           买
      dp_table = [[最大利润,  最低股价的股票]...]
      :param prices:
      :return:
      """
      dp_table = [[0, 0] for _ in range(len(prices))]
  
      dp_table[0] = [0, 7]
      for i in range(1, len(prices)):
          # 最大利润 = max(prev最大利润, cur股价 - prv持有股价)
          dp_table[i][0] = max(dp_table[i-1][0], prices[i] - dp_table[i-1][1])
          # 持有股票 = min(prev持有股价, cur股价)
          dp_table[i][1] = min(dp_table[i-1][1], prices[i])
      return dp_table
  
  

• 买股票的最佳时机2

  def max_profit2(prices):
      """
      - 在不重复购买的情况下, 可以任意操作
      - 最大利润 = 交易操作的累计和
  
      这道题和上一道题的区别在于, 因为是多次操作, 那我们要寻找的不是最低价的股票
      而是要得到每次买卖操作的最大利润.
      同样的, 持有的股票不能算作当前利润, 因为股票终究是要卖出才能得到最大收益.
      所以要分两种情况:
                     持有股票: 最大利润 = 交易所得利润(同时持有股票)
                     不持有股票: 最大利润 = 交易所得利润 + 上一阶段如果持有股票 - 当前股价
  
                     卖     买
      dp_table = [[不持有, 持有]...]
      :param prices:
      :return:
      """
      dp_table = [[0, 0] for _ in range(len(prices))]
  
      dp_table[0] = [0, -prices[0]]
  
      for i in range(1, len(prices)):
          # 不持有的情况: 1. 上一次没有持有, 不存在卖的操作; 2. 上一次持有, 这次卖了
          dp_table[i][0] = max(dp_table[i-1][0], dp_table[i-1][1] + prices[i])
          # 持有的情况: 1. 上一次持有, 不存在买的操作; 2. 上一次不持有, 这次买了
          dp_table[i][1] = max(dp_table[i-1][1], dp_table[i-1][0] - prices[i])
      return dp_table[-1][0]
  
  

双指针

• 左右指针

  强调两个指针相对的位置

  • 二分查找
  • 两数之和
  • 链表翻转
  • 滑动窗口

• 快慢指针

  强调两个指针移动速度, 或者叫步长

  • 判断链表中是否有环
  • 链表中点
  • 数组去重
  • 快排

题集

• 快慢指针

  • 删除有序数组中的重复项

    def drop_duplicates(nums):
        """
        移除数组中的重复元素
    
        - 直接对nums进行修改
        :param nums:
        :return:
        """
        # 指示当前需要判断重复的元素的索引
        slow = 1
    
        # 用来遍历数组, 查找与slow值不同的元素
        # 如果找到了, slow的值将被赋值为fast代表的值
        fast = 1
    
        while fast < len(nums):
            if nums[fast-1] != nums[fast]:
                nums[slow] = nums[fast]
                slow += 1
            fast += 1
    
        return nums, slow
    
    
    

  • 环形链表

    def has_cycle(head):
        slow = fast = head
    
        # 如果最终fast为null, 说明当前到达链表的末端
        # 说明当前链表没有环
        while fast:
            fast = fast.next.next
            slow = slow.next
            if slow == fast:
                return True
        return False
    

  • 环形链表2

    def detect_cycle(head):
        """
        slow = a + b
        fast = a + b + c + b
    
        fast = 2slow
    
           a + b + c + b = 2a + 2b
        => c = a
        :param head:
        :return:
        """
        slow = fast = head
        while fast:
            fast = fast.next.next
            slow = slow.next
            if slow == fast:
                # 停止的位置就是快慢指针相遇点
                break
    
        # 当前无环
        if not fast:
            return None
    
        slow = head
        while slow != fast:
            # 因为a=c, slow和fast以同样的速度前进, 相交点就是入环点
            slow = slow.next
            fast = fast.next
        return slow
    
    

• 左右指针

  • 验证回文串

    def is_palindrome(string):
        left = 0
        right = len(string) - 1
        while right >= left:
            while not string[left].isalpha():
                left += 1
    
            while not string[right].isalpha():
                right -= 1
    
            if string[left].lower() == string[right].lower():
                left += 1
                right -= 1
            else:
                print("break", left, right)
                break
    
        return left-1 == right+1 or left-1 == right
    

  • 合并两个有序数组

    略

  • 二分查找

    def binary_search(nums, target):
        left = 0
        right = len(nums) - 1
    
        while left <= right:
            mid = (left + right) // 2
            if nums[mid] == target:
                return mid
            elif nums[mid] < target:
                left = mid + 1
            elif nums[mid] > target:
                right = mid - 1
    
        return -1