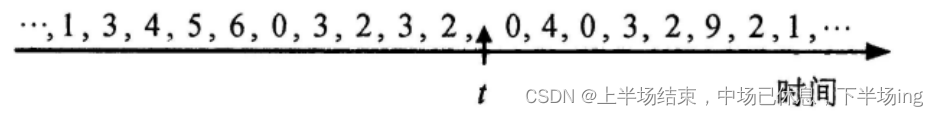个人主页：平行线也会相交
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创
收录于专栏【数据结构初阶（C实现）】

字符串匹配算法

在学习这个算法之前，我们先来看看什么时字符串匹配算法，简单来说有一个主串和一个子串，查找子串在主串的位置，然后返回这个位置的下标。
想要实现这个功能其实有很多方法，比较有名的算法有两种：一种是BF算法又称暴力算法，另一种就是KMF算法。

BF算法

BF算法：思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配，如果相等，则继续比较S的第二个字符和T的第二个字符；如果不相等，则比较S的第二个字符和T的第一个字符，依次比较下去，直到得出最后的酦醅结果。
举个例子：

代码实现

#define _CRT_SECURE_NO_WARNINGS 1
//BF算法

#include<assert.h>

#include<stdio.h>

//str为主串，sub为子串
int BF(char* str, char* sub)
{
	assert(str != NULL && sub != NULL);
	if (str == NULL || sub == NULL)
		return -1;
	int lenStr = strlen(str);
	int lenSub = strlen(sub);
	int i = 0;
	int j = 0;
	while (i < lenStr && j < lenSub)
	{
		if (str[i] == sub[j])
		{
			i++;
			j++;
		}
		else
		{
			i = i - j + 1;
			j = 0;
		}
	}
	if (j >= lenSub)//如果j>=lenSub说明子串遍历完成，即匹配成功，返回i的下标。
	{
		return i - j;
	}
	//不存在直接返回-1
	return -1;
}

int main()
{
	printf("%d\n", BF("ababcabcdabcde", "abcd"));
	printf("%d\n", BF("ababcabcdabcde", "abcdf"));
	printf("%d\n", BF("ababcabcdabcde", "ab"));
	return 0;
}

KMP算法

KMP算法就是对BF算法是一种对BF算法的改进，该算法核心就是可以利用匹配失败后的信息，尽量减少模式串与字串的匹配次数以到达快速匹配的目的（具体shi）。
KMP与BF算法的区别就是KMP算法主串的并不会回退；并且j不会移动到0号位置，而是移动到一个特定的位置。
我们直接来举个例子：

此时i和j位置的字符不匹配了。此时i是不进行回溯的，而是要对j进行回溯，那么j应该回溯到哪个位置呢？

由于每个位置要回溯的位置可能不一样，所以就引出了next数组。即用next[j]=k来表示。不同的j对应一个K值。这个K就是将来j要进行回溯的位置。如上图我们求的是当j=5的时候，K的值就是2，即将来j要回溯到下标为2的位置。即next[5]=2;。再比如说，当j是4的时候，K的值就是1，即next[4]=1;。

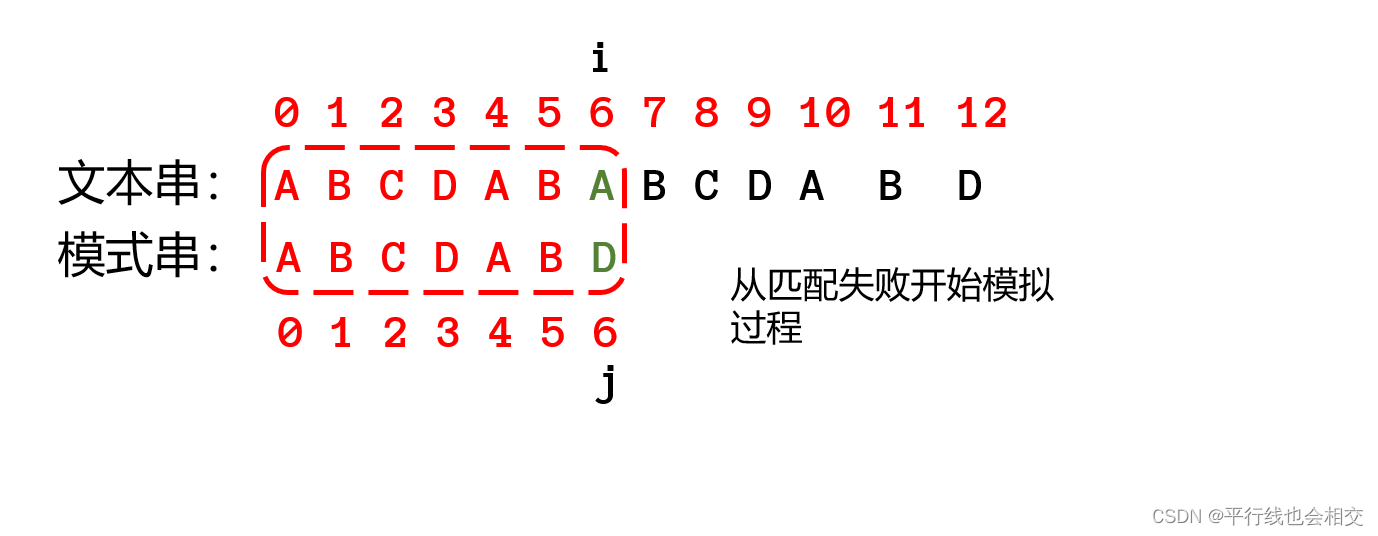
关于K值求取的规则如下：

1.找到匹配成功部分的两个相等的真串（不包含本身），一个以下标0开始，另一个j-1下标结束。
2.无论是什么数据，如果我们是从0开始计数（这里按照数组下标从0开始的习惯所以从0开始计数），那么next[0]=-1;next[1]=0；如果我们从1开始计数，那么next[0]=0;next[1]=1。

来练习一下：
"a b a b c a b c d a b c d e ",求其next数组。
答案如下图：

代码实现

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<string.h>

void GetNext(char* sub, int* next, int lenSub)
{
	next[0] = -1;
	next[1] = 0;
	int i = 2;
	int k = 0;
	while (i < lenSub)
	{
		if (k == -1 || sub[i - 1] == sub[k])
		{
			next[i] = k + 1;
			i++;
			k++;
		}
		else
		{
			k = next[k];
		}
	}
}

int KMP(char* str, char* sub, int pos)
{
	assert(str != NULL && sub != NULL);
	int lenStr = strlen(str);
	int lenSub = strlen(sub);
	if (lenStr == 0 || lenSub == 0)
		return -1;
	if (pos < 0 || pos >= lenStr)
		return -1;

	int* next = (int*)malloc(sizeof(int) * lenSub);
	assert(next != NULL);

	GetNext(sub, next, lenSub);

	int i = pos;//遍历主串
	int j = 0;//遍历子串

	while (i < lenStr && j < lenSub)
	{
		if (j == -1 || str[i] == sub[j])
		{
			i++;
			j++;
		}
		else
		{
			j = next[j];
		}
	}
	if (j >= lenSub)
	{
		return i - j;
	}
	return -1;
}

int main()
{

	printf("%d\n", KMP("ababcabcdabcde", "abcd", 0));
	printf("%d\n", KMP("ababcabcdabcde", "abcdf", 0));
	printf("%d\n", KMP("ababcabcdabcde", "ab", 0));
	return 0;
}

nextval数组改进

下面来看nextval数组的求解规则。

1.无论是什么数据，nextval[0]=-1;(这里还是默认数组的习惯从0开始计数)。如果是从1开始计数，则nextval[0]=0;。
2.从第二位开始，我们用next[i]值对应的字符与i值对应的字符进行比较。如果相等，则nextval[i]就等于next[i]值对应字符的nextval[i]值；如果不相等，则nextval[i]值就等于当前字符对应的next值。

我们还是来进行举例：

求模式串"a b c a a b b c a b c a a b d a b"。

下面来看详细过程：
第一个字符a对应的nextval[0]一定为-1（按照从0开始计数的话）。即nextval[0]=-1;
第二个字符b的next值即next[1]=0;所以第二个字符和下标为0的字符进行比较。发现不相等，所以nextval[1]=第二个字符所对应的next值，即nextval[1]=0;。
第三个字符c的next值即next[2]=0;所以第三个字符和下标为0的字符进行比较。发现不相等，所以nextval[2]=第三个字符所对应的next值，即nextval[2]=0;。
第四个字符a的next值即next[3]=0;所以第四个字符和下标为0的字符进行比较。发现相等了，所以nextval[3]=下标为0的字符所对应的nextval值，在这里就是nextval[3]=nextval[0]。
第五个字符a的next值即next[4]=1;所以第五个字符a和下标为1的字符b进行比较。发现不相等，所以nextval[4]=当前字符(即指的是第五个字符)所对应的next值，所以最终nextval[4]=next[4]=1。
依此类推进行分析，所以最终该串的nextval数组就如上图所示。

好了，以上就是关于字符串BF和KMP算法的一个记录。
就到这里吧，各位，再见啦！！！