一.快速排序

1.基本介绍

快速排序（Quicksort）由英国计算机科学家Tony Hoare于1959年发明，是一种经典的排序算法，被广泛应用于计算机科学领域。快速排序（Quick Sort）是一种常见的基于比较的排序算法，也是最常用的排序算法之一。

快速排序是一种

排序方法	最好	平均	最坏	空间复杂度	稳定性
快速排序	O(n * log(n))	O(n * log(n))	O(n^2)	O(log(n)) ~ O(n)	不稳定

稳定性:如果a原本在b前面，并且a=b,排序之后a仍然在b的前面,那么就成这个算法是稳定的,否则就是不稳定的;

2.基本思想

以下是快速排序的基本思路

选择一个基准元素（pivot）。
将序列中所有小于基准元素的元素放在基准元素的左侧，所有大于基准元素的元素放在右侧。
递归地对基准元素左侧和右侧的子序列进行排序。
递归结束后，整个序列就变得有序。

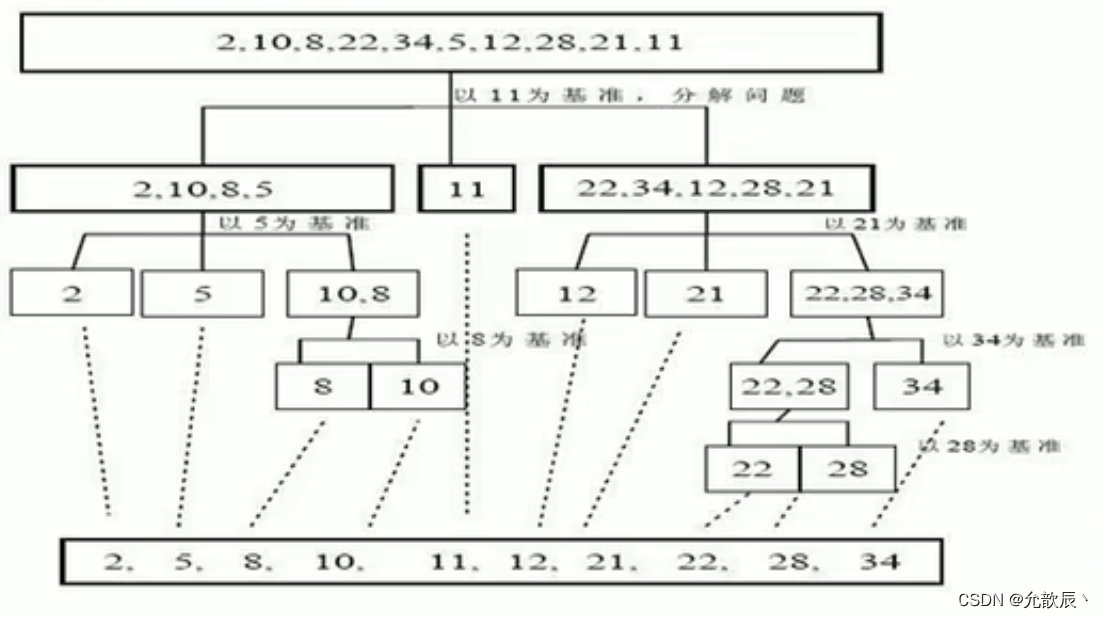
以下介绍的各种快排的思路都大致一样的,主要就是在划分的策略不一样,基本思路都是一样的

二.Hoare快排

0.前情知识

1.交换数组中的两个元素

    public static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

2.指定范围的插入排序

    /**
     * 将区间[left,right]的元素进行插入排序
     *
     * @param arr
     * @param left
     * @param right
     */
    private static void insertSortInterval(int[] arr, int left, int right) {
        for (int i = left + 1; i <= right; ++i) {
            for (int j = i; j > left && arr[j] < arr[j - 1]; --j) {
                swap(arr, j, j - 1);
            }
        }
    }

1.基本思路

我们这里重点介绍分区的方法,因为这几个快速排序的区别主要就是在分区的方法,快速排序的基本思路我们在上面已经说出,在这里就不赘述了.

这里来讲解分区的方法,也就是partition部分的代码.

其实简而言之而很好理解,我们选取左端的值作为中轴值,定义两个指针i,j, j从右端向左进行遍历,当遍历到比中轴值(pivot)小的数时候,停止,i从左端向右进行遍历,当遍历到比中轴值大的时候,停止,这个时候交换位置i和位置j的元素 ,当i==j的时候,停止循环,然后交换位置left和i(j)的元素,此时i左边的元素比arr[i]小,i右边的元素比arr[i]大,返回此时的位置i.

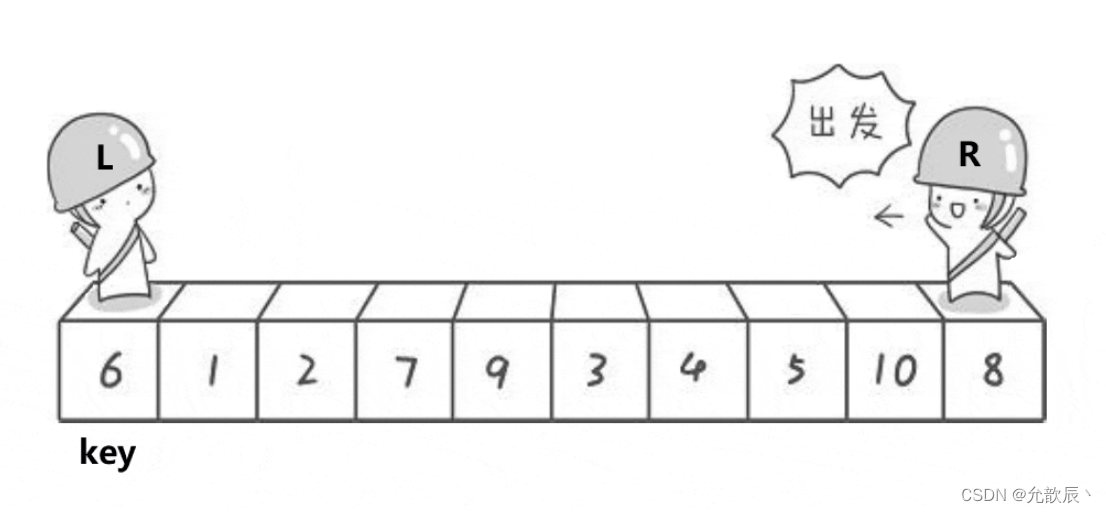
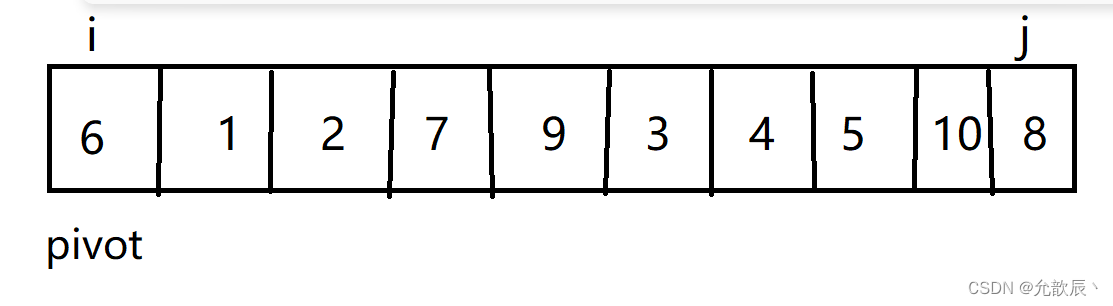
初始情况:

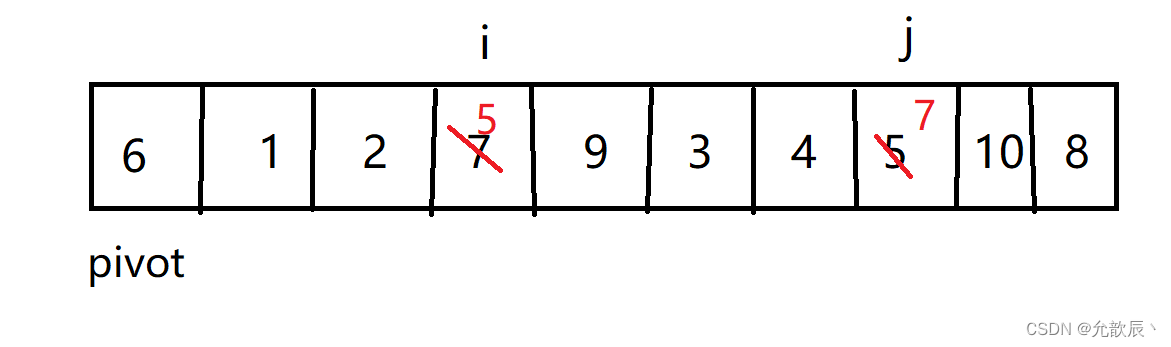
第一次交换

第二次交换

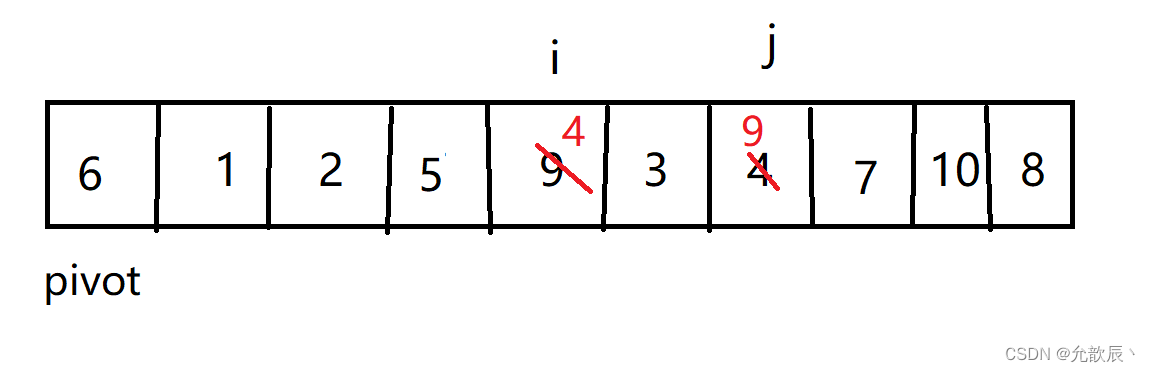
结束循环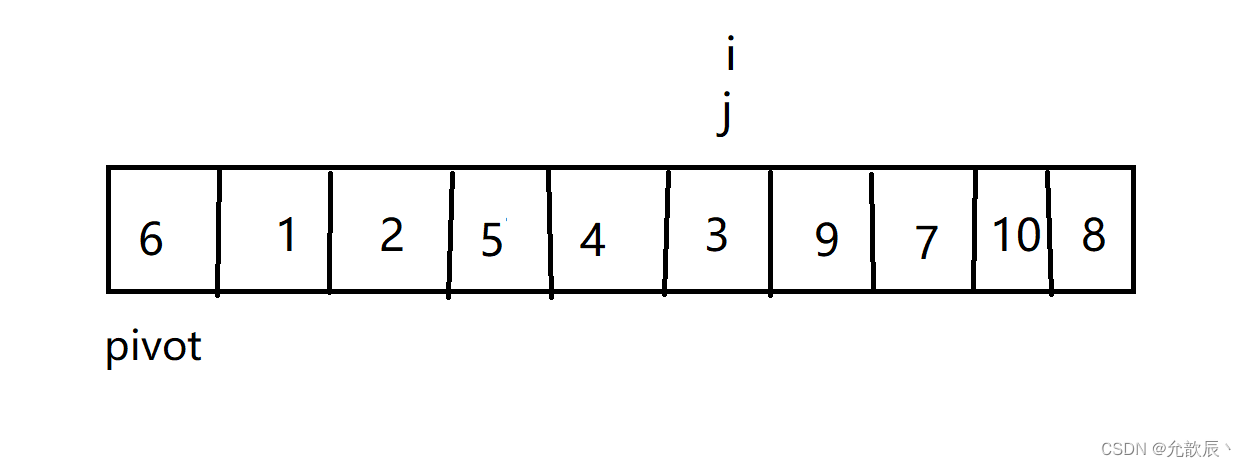

中轴值交换操作

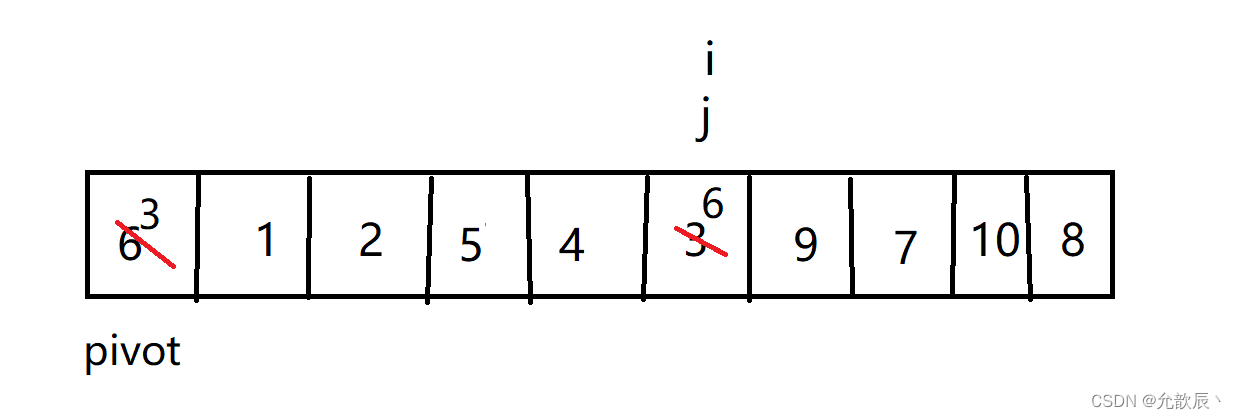
此时pivot=6左边的元素都比6的值小,右边的值都比pivot大了,这样一次分区结束.

2.代码实现

    //Hoare版快排
    public static void quickSortHoare(int[] arr) {
        quickSortHoareInternal(arr, 0, arr.length - 1);
    }

    private static void quickSortHoareInternal(int[] arr, int left, int right) {
        if (left >= right) {
            return;
        }
        int pivotIndex = partitionHoare(arr, left, right);
        quickSortHoareInternal(arr, left, pivotIndex - 1);
        quickSortHoareInternal(arr, pivotIndex + 1, right);

    }

    private static int partitionHoare(int[] arr, int left, int right) {
        //选取最左边的元素作为中轴值
        int pivot = arr[left];
        int i = left, j = right;
        while (i < j) {
            //从右边找到比pivot小的元素
            while (i < j && arr[j] >= pivot) {
                j--;
            }

            //从左边找到比pivot大的元素
            while (i < j && arr[i] <= pivot) {
                i++;
            }
            swap(arr, i, j);

        }
        //将中轴值元素和i==j时的位置交换,此时i左边的元素都比pivot小,右边都比pivor大
        swap(arr,i,left);
        return i;

    }

3.优化思路

优化一:学习过插入排序我们知道,对于小数组来说,插入排序的效率可谓是十分的高,对于长度小于64的小数组,我们不妨直接使用插入排序进行排序

    private static void quickSortHoareInternal(int[] arr, int left, int right) {
        if (right - left <= 64) {
            insertSortInterval(arr, left, right);
            return;
        }
        int pivotIndex = partitionHoare(arr, left, right);
        quickSortHoareInternal(arr, left, pivotIndex - 1);
        quickSortHoareInternal(arr, pivotIndex + 1, right);

    }

优化二:我们来考虑这样一个问题,当我们需要排序的数组基本有序的时候,我们每次还是选择数组的第一个元素作为中轴值,这样我们要进行递归O(n)的空间复杂度,这个时候快速排序就退化为了冒泡排序,时间复杂度为O( $n^{2}$ )

那我们该如何选取中轴值呢?

第一种方法:随机选取中轴值

生成一个范围为[left,right]的随机数生成下标为index,将index与left交换,之后就和我们之前的代码一模一样了.

    private static int partitionHoare(int[] arr, int left, int right) {
        //优化,选取随机值
        int index = ThreadLocalRandom.current().nextInt(left, right + 1);
        swap(arr, index, left);
        int pivot = arr[left];
        int i = left, j = right;
        while (i < j) {
            //从右边找到比pivot小的元素
            while (i < j && arr[j] >= pivot) {
                j--;
            }

            //从左边找到比pivot大的元素
            while (i < j && arr[i] <= pivot) {
                i++;
            }
            swap(arr, i, j);

        }
        swap(arr, i, left);
        return j;

    }

第二种方法:三数中值分割法

我们都希望我们选取的中轴值恰好为待排序数组的中值,这样递归的次数一定是最少的,因此我们可以使用三数取中的方法来进行估算中值(当然最坏情况也可能取到第二小的情况,但概率相对来说很小),我们通常选取左端,右端,中心位置上的三个元素的中值作为枢纽元素.来看代码实现

    public static void median(int[] arr, int left, int right) {
        //中间索引下标,相当于(left+right)/2
        int center = left + ((right - left) >> 1);
        if (arr[center] < arr[left]) {
            swap(arr, center, left);
        }
        if (arr[right] < arr[left]) {
            swap(arr, right, left);
        }
        if (arr[right] < arr[center]) {
            swap(arr, center, right);
        }
        swap(arr, left, center);//此时中值被交换到了最左边位置
    }

    private static int partitionHoare(int[] arr, int left, int right) {
        median(arr,left,right);
        int pivot = arr[left];
        int i = left, j = right;
        while (i < j) {
            //从右边找到比pivot小的元素
            while (i < j && arr[j] >= pivot) {
                j--;
            }

            //从左边找到比pivot大的元素
            while (i < j && arr[i] <= pivot) {
                i++;
            }
            swap(arr, i, j);

        }
        swap(arr, i, left);
        return j;

    }

三.挖坑法快排(校招中适用)

1.基本思路

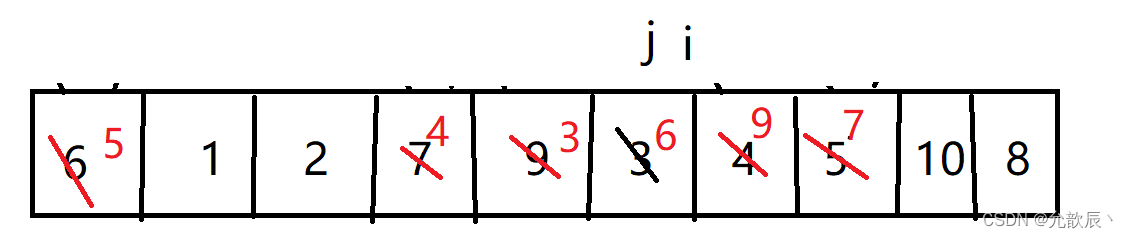
挖坑法快排的基本思路:我们先把pivot的值保留下来,此时相当于在pivot位置(也就是left位置)挖了一个坑,然后我们开始循环,循环条件和Hoare快排一样,j从右端向左找到比pivot小的元素,将arr[j]的值填到之前挖的坑(也就是left位置),然后在j位置挖一个坑,i从左端开始寻找比pivot大的元素,找到后将它填到j位置(之前挖的坑),以此类推,最终i==j,这是挖的最后一个坑,将pivot值填入到arr[i]的位置,此时我们挖坑填坑操作完成,arr[i]左边的元素都比它小,右边的元素都比它大

可以看出来的是:相对于Hoare快排来说,交换的次数大大减少

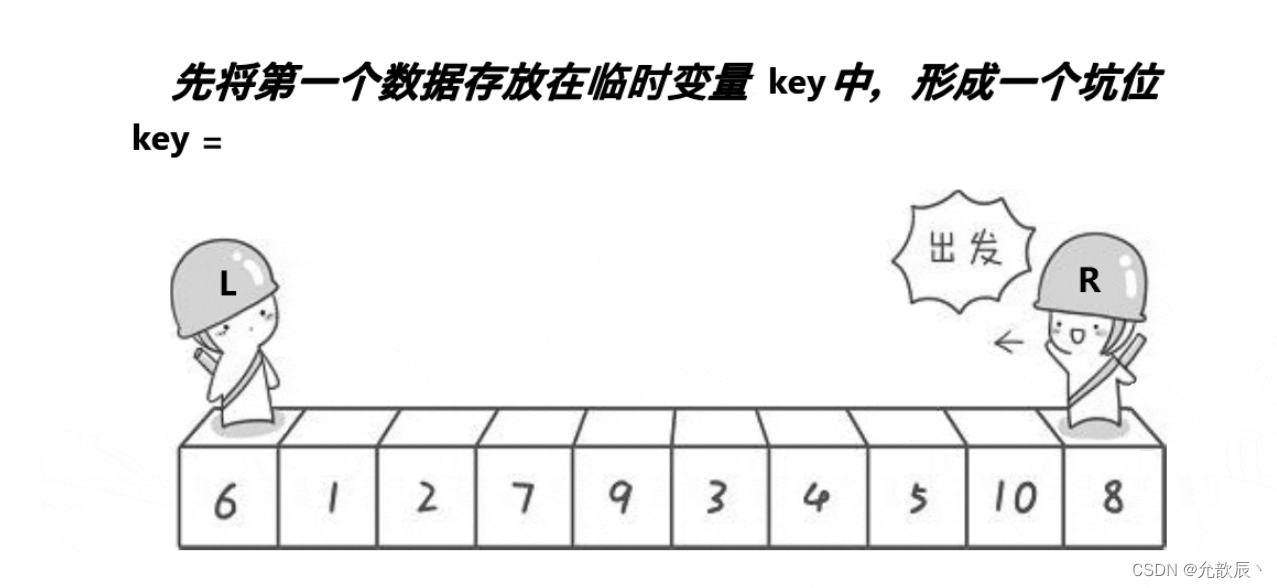
第一次挖坑填坑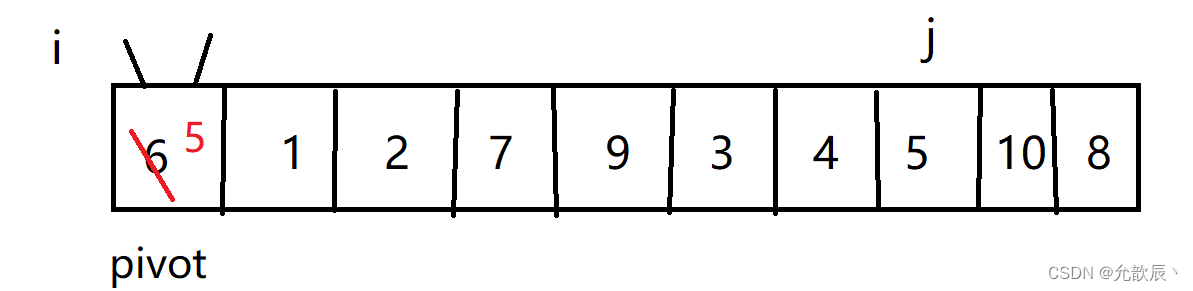

第二次挖坑填坑

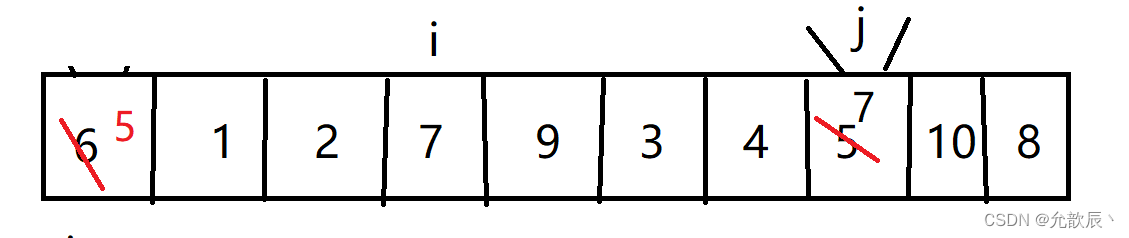
第三次挖坑填坑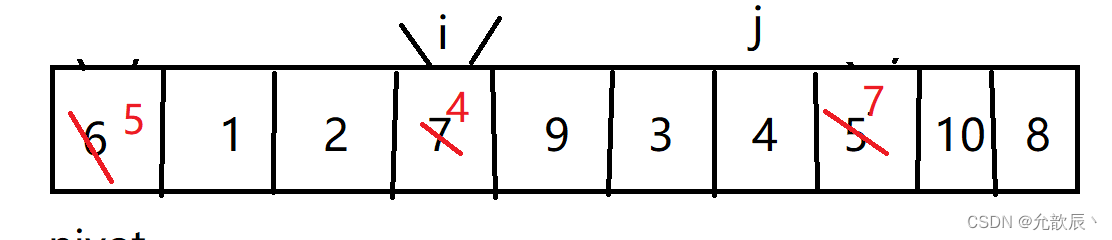

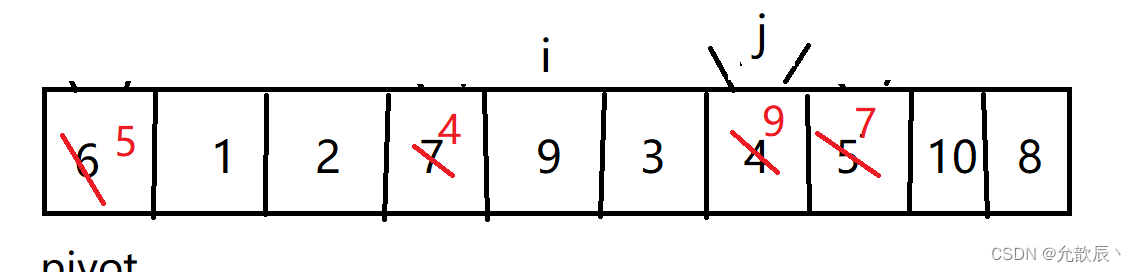
第四次挖坑填坑

第五次挖坑填坑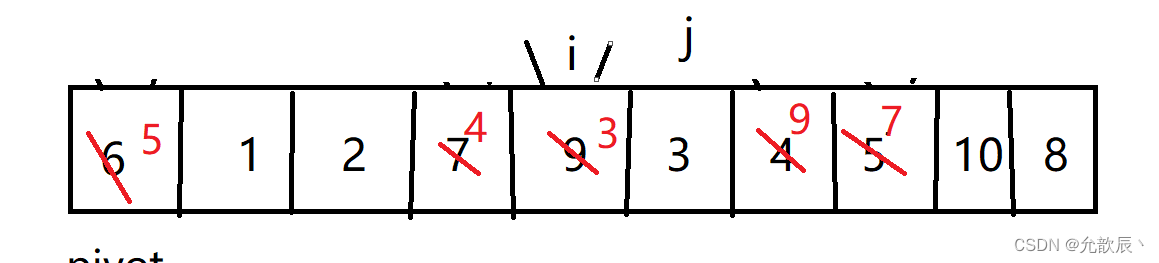

最后一次arr[i]=pivot

2.代码实现

优化的地方和Hoare快排一样,这里直接给出优化之后的代码,这里采用了随机值选取中轴值的方法.

    //挖坑法快排
    public static void quickSortHole(int[] arr) {
        quickSortHoleInternal(arr, 0, arr.length - 1);
    }

    private static void quickSortHoleInternal(int[] arr, int left, int right) {
        if (right - left <= 64) {
            insertSortInterval(arr, left, right);
            return;
        }
        int pivotIndex = partitionByHole(arr, left, right);
        quickSortHoleInternal(arr, left, pivotIndex - 1);
        quickSortHoleInternal(arr, pivotIndex + 1, right);

    }

    private static int partitionByHole(int[] arr, int left, int right) {
        //优化,选取随机值
        int index = ThreadLocalRandom.current().nextInt(left, right + 1);
        swap(arr, index, left);
        int pivot = arr[left];
        int i = left, j = right;
        while (i < j) {
            //从右边找到比pivot小的元素
            while (i < j && arr[j] >= pivot) {
                j--;
            }
            //将这个小的元素放到左边
            arr[i] = arr[j];
            //从左边找到比pivot大的元素
            while (i < j && arr[i] <= pivot) {
                i++;
            }
            //将这个大的元素放到右边
            arr[j] = arr[i];

        }
        //最后一定是i==j退出
        arr[j] = pivot;
        return j;

    }

四.二路快排

1.基本思路

二路快排其实就是分区进行,也是国外教材上实现的快排的方法(算法4),总体的效率要比挖坑法和Hoare法要快一些.

主要就是维护两个分区,一个分区的值全比pivot的值小,另一个分区的值大于等于pivot的值,最终分区完毕之后的结果如下图所示:

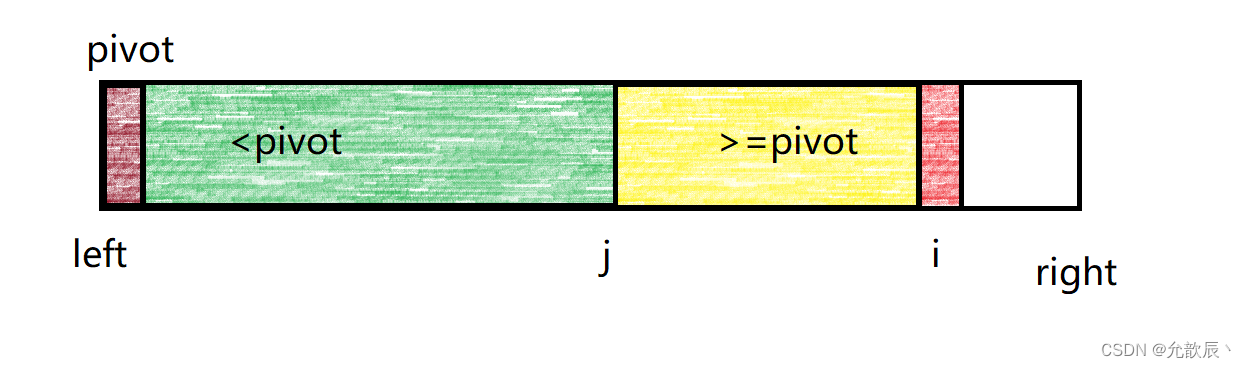
维护的小于pivot的区间为[left+1,j] 维护的大于等于pivot的区间为[j+1,i-1] 其中i指向的是正在遍历到的元素位置,j指向的是小于pivot区间的最后位置,j+1是大于等于pivot的开始位置.白色的区域表示未遍历到的区域.

现在我们来讨论两种情况,一种是当arr[i]>=pivot的时候,这个时候我们只需要将i指向位置的变为黄色,也就是将i++处理,这是时候大于等于pivot的区间就相当于增加了一个元素

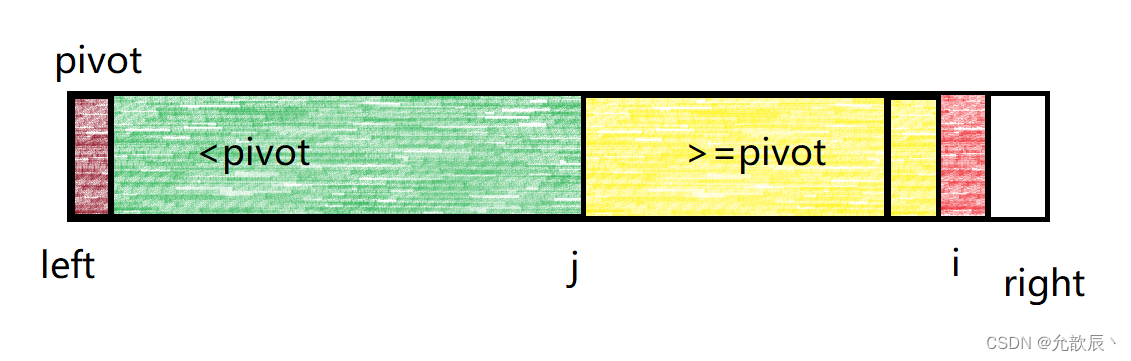
另一种是arr[i]<pivot的时候,这个时候我们只需要将arr[i]的元素和arr[j+1]的元素进行交换,并且要将j++,然后将i++,这样小于pivot的区间就增加了一个元素.

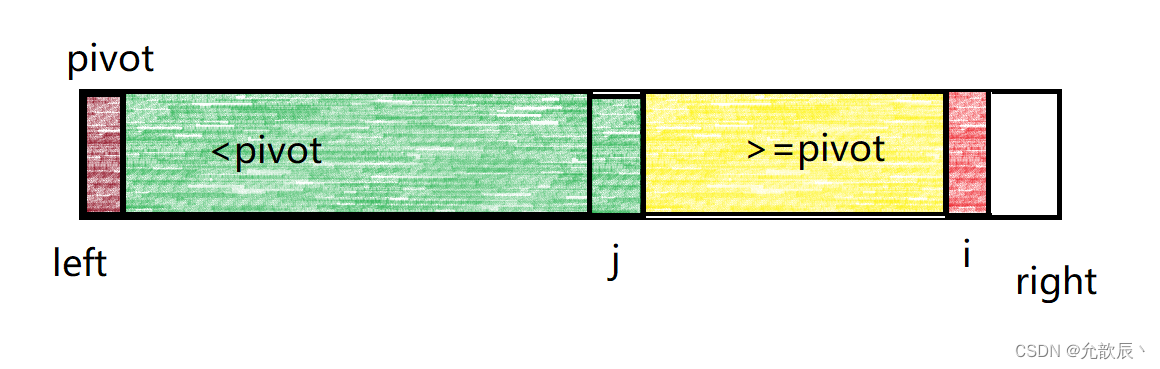
这样一种循环下去,直到i遍历完最后一个元素的时候,这个时候我们将j位置的元素和left位置的元素进行交换,这样就实现了pivot元素左边的元素小于pivot,pivot右边的元素大于等于pivot.

具体的代码实现看下面

2.代码实现

    // 算法4的分区快排
    public static void quickSort(int[] arr) {
        quickSortInternal(arr, 0, arr.length - 1);
    }

    private static void quickSortInternal(int[] arr, int left, int right) {
        if (right - left <= 64) {
            insertSortInterval(arr, left, right);
            return;
        }
        int p = partition(arr, left, right);
        quickSortInternal(arr, left, p - 1);
        quickSortInternal(arr, p + 1, right);
    }

    //二路快排,左半部分小于pivot,右半部分大于等于pivot
    private static int partition(int[] arr, int left, int right) {
        int randomIndex = ThreadLocalRandom.current().nextInt(left, right + 1);
        swap(arr, left, randomIndex);
        int pivot = arr[left];
        // arr[l + 1..j] < pivot
        int j = left;
        // arr[j + 1..i) >= pivot
        for (int i = left + 1; i <= right; i++) {
            if (arr[i] < pivot) {
                swap(arr, j + 1, i);
                j++;
            }
        }
        swap(arr, j, left);
        return j;
    }

3.优化思路

当我们出现大量相同元素的时候,这个时候二路快排的其实效率并不是很快,因为要进行很多次无用的递归处理,这个时候我们是否可以考虑单独分成一个分区是等于pivot的呢?确实是可以实现的,这个时候我们采用三路快排的方式,可以很大程度上解决我们所说的问题

五.三路快排

1.基本思路

三路快排的实现思路和二路快排的实现思路基本一样,只不过多维护一个等于pivot的区间,这样我们进行递归的时候,就没必要递归的进行等于pivot的区间部分,大大提高了快速排序的效率.

以下为三路快排分区的格局:

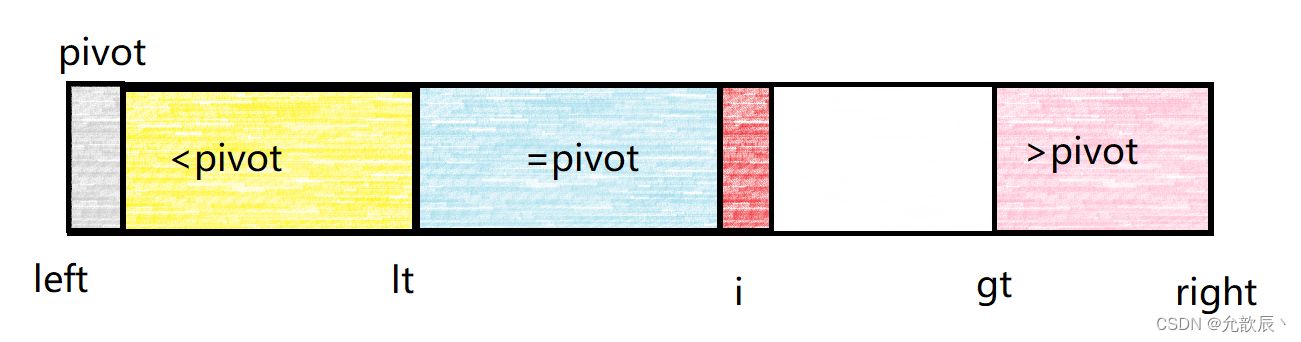
维护小于pivot的区间为[left,lt],维护等于pivot的区间为[lt+1,i-1],维护大于pivot的区间为[gt,right]. i表示正在遍历到的位置索引,当i>=gt的时候遍历结束白色的区域表示未遍历到的区域.

三路快排有三种情况需要考虑

1.当arr[i]>pivot的时候,我们可以将arr[i]与arr[lt+1]进行交换,并且将i++,这个时候小于pivot的区间增加

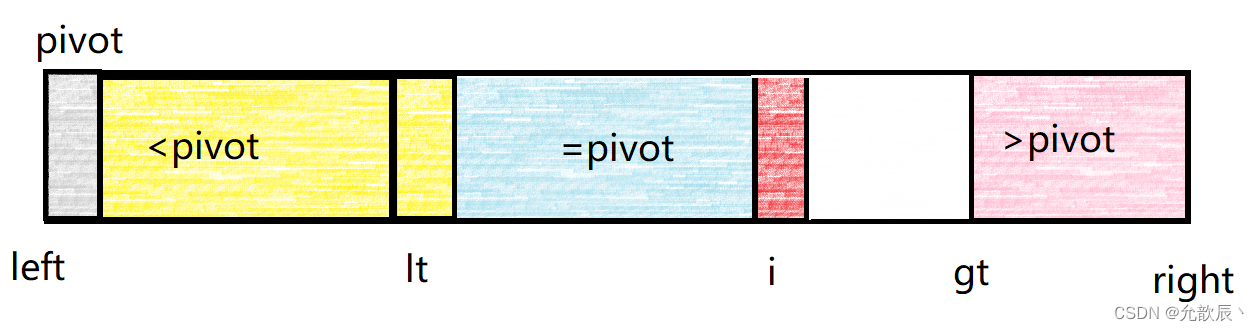
2.当arr[i]==pivot的时候,我们直接将i++即可,这个时候等于pivot的区间增加,处理结束

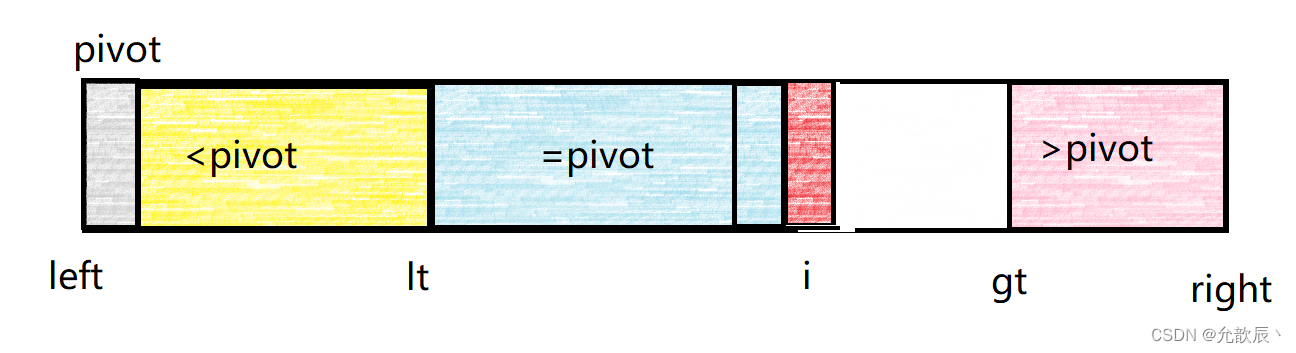
3.当arr[i]>pivot的时候,我们可以将arr[i]与arr[gt-1]进行交换,并且gt--,表示大于pivot的区间增加.这个时候i不需要增加,因为交换的区域是白色的区域,没有遍历到的,我们需要下一次进行判断

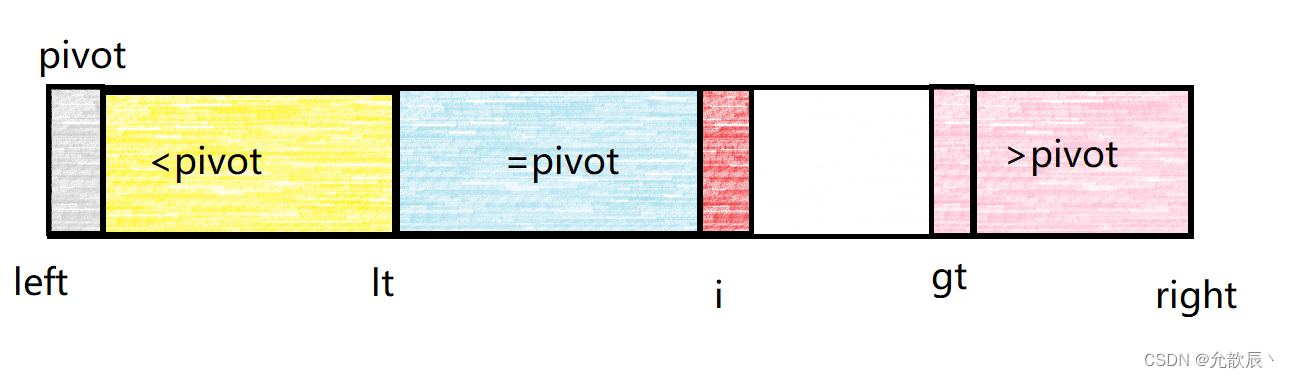
最终当i==gt的时候循环结束,我们将arr[left]和arr[lt]的元素进行交换

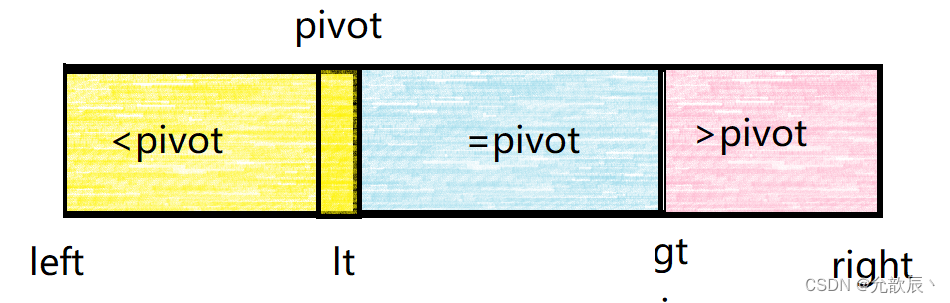
递归的条件现在为left-->lt-1 gt-->right

2.代码实现

    //三路快排(对于处理含有重复元素的数组很有效)
    public static void quickSort3(int[] arr) {
        quickSort3Internal(arr, 0, arr.length - 1);
    }

    private static void quickSort3Internal(int[] arr, int left, int right) {
        if (right - left <= 64) {
            insertSortInterval(arr, left, right);
            return;
        }
        int radomIndex = ThreadLocalRandom.current().nextInt(left, right + 1);
        //此时left位置为中轴值
        swap(arr, left, radomIndex);
        int pivot = arr[left];
        //区间[left+1,lt]的值<pivot
        int lt = left;
        //区间[gt,right]的值>pivot
        int gt = right + 1;
        //区间(lt,gt)的元素==pivot
        //目前遍历到的位置
        int i = left + 1;
        //终止条件i与gt重合
        while (i < gt) {
            if (arr[i] < pivot) {
                swap(arr, i, lt + 1);
                lt++;
                i++;
            } else if (arr[i] > pivot) {
                swap(arr, i, gt - 1);
                gt--;
            } else {//相等的情况
                i++;

            }
        }
        swap(arr, left, lt);
        quickSort3Internal(arr, left, lt - 1);
        quickSort3Internal(arr, gt, right);

    }

六.非递归快排的实现

1.思路分析

其实非递归的快排也是很好实现的,我们仔细观察之前的代码可以发现,其实快速排序的代码是很像二叉树的前序遍历的,都是先处理,然后向左进行递归处理,向右进行递归处理:对二叉树递归和迭代实现不清楚的可以看这篇博客:树的遍历方式(前中后,层序遍历,递归,迭代,Morris遍历)

我们在实现迭代二叉树前序遍历的时候采用了栈这种结构,我们在这里也要借用栈来实现快速排序的非递归实现.那我们在栈中要保存什么信息呢,我们在进行递归实现快速排序的时候,每一次递归的都是left和right进行改变的递归,这里我们肯定是要保存left和right的,然后取出来left和right进行分区(partition)处理,但是我们需要注意的是保存的顺序应该时反向的,也就是先保存right,再保存left,因为栈性质:先进后出,这样才能保证和递归的顺序是一致的.

具体看代码的实现.

2.代码实现

    //非递归快排(挖坑)
    public static void quickSortNoRecursion(int[] arr) {
        LinkedList<Integer> stack = new LinkedList<>();
        stack.push(arr.length - 1);
        stack.push(0);
        while (!stack.isEmpty()) {
            Integer left = stack.pop();
            Integer right = stack.pop();
            if (right - left <= 64) {
                insertSortInterval(arr, left, right);
                continue;
            }
            int pivotIndex = partitionByHole(arr, left, right);
            stack.push(right);
            stack.push(pivotIndex + 1);
            stack.push(pivotIndex - 1);
            stack.push(left);

        }


    }
    //这里使用的挖坑法快排的划分方式,也可以使用别的快排的划分方式
    private static int partitionByHole(int[] arr, int left, int right) {
        //优化,选取随机值
        int index = ThreadLocalRandom.current().nextInt(left, right + 1);
        swap(arr, index, left);
        int pivot = arr[left];
        int i = left, j = right;
        while (i < j) {
            //从右边找到比pivot小的元素
            while (i < j && arr[j] >= pivot) {
                j--;
            }
            //将这个小的元素放到左边
            arr[i] = arr[j];
            //从左边找到比pivot大的元素
            while (i < j && arr[i] <= pivot) {
                i++;
            }
            //将这个大的元素放到右边
            arr[j] = arr[i];

        }
        //最后一定是i==j退出
        arr[j] = pivot;
        return j;

    }