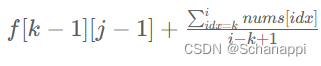今天就这一道题, 但还是有难度的

单词就是物品, 字符串s就是背包, 单词能否组成字符串s, 就是问物品能不能把背包装满

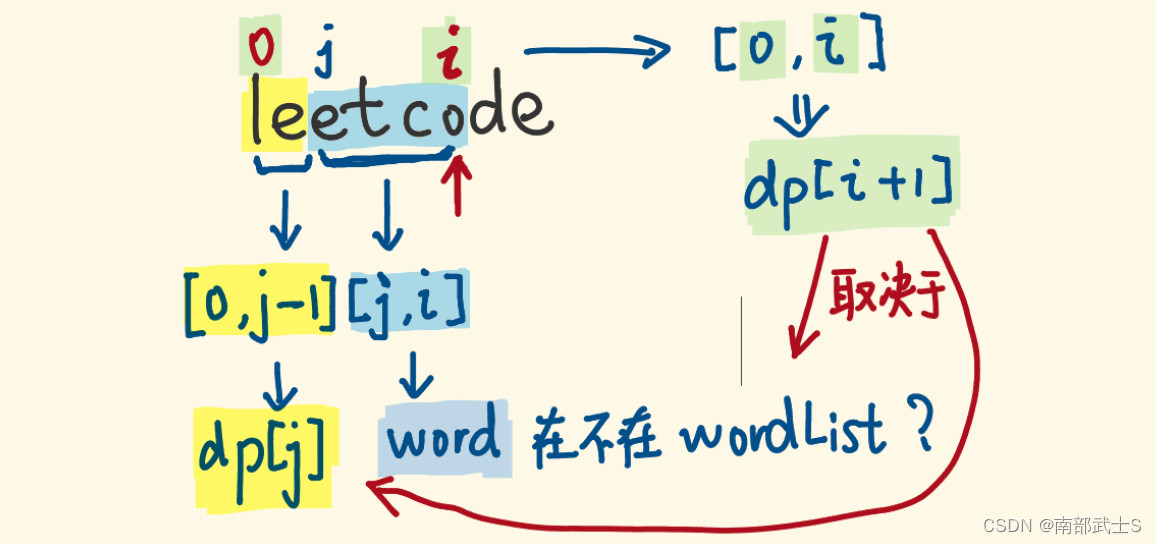
1. 确定dp数组含义: 字符串长度为i的话, dp[i]为true, 表示可以拆分, j是分割指针
2. 确定递推公式: 如果确定dp[j]是true, 且[j , i]这个区间的子串出现在字典里, 那么dp[i]一定是true, 所以递推公式是if([j,i]这个区间的子串出现在字典里 && dp[j]是true), 那么dp[i] = true
3. 初始化: dp[i]的状态依靠dp[j]是否为true, 所以dp[0]一定要为true
4. 遍历顺序都可以, 但由于是要求子串, 最好先背包

(细节: 需要用一个hashset来判断单词是否在set中)

 

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        //利用hashset来判断是否contain
        HashSet<String> set = new HashSet<>(wordDict);
        boolean[] dp = new boolean[s.length() + 1];

        //初始化
        dp[0] = true;
        //先遍历背包, 那么就是背包的大小
        for(int i = 1; i <= s.length(); i++){
            //j是分割点, 所以就不用等于i了
            ///如图, j是i前一个, 所以从0开始,不用等于i
            for(int j = 0; j < i; j++){
                //开始判断条件, dp[j]是否合法&&是否在set里
                if(dp[j] && set.contains(s.substring(j, i))){
                    dp[i] = true;
                }
            }
        }
        //i是字符串的长度, 所以这里一样
        return dp[s.length()];
    }
}

多重背包

有n种物品和一个容量为v的背包, 第i中物品最多有MJ件可用, 没见耗费的空间是Ci, 价值是Wi

(其实和01背包很像, 把这里的m件摊开来就是01背包了)

就是在01背包的基础上多加个for循环遍历物品个数

public void testMultiPack2(){
    // 版本二：改变遍历个数
    int[] weight = new int[] {1, 3, 4};
    int[] value = new int[] {15, 20, 30};
    int[] nums = new int[] {2, 3, 2};
    int bagWeight = 10;

    int[] dp = new int[bagWeight + 1];
    for(int i = 0; i < weight.length; i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            // 以上为01背包，然后加一个遍历个数
            for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) { // 遍历个数
                dp[j] = Math.max(dp[j], dp[j - k * weight[i]] + k * value[i]);
            }
            System.out.println(Arrays.toString(dp));
        }
    }
}