题目描述
给定数组 nums 和一个整数 k 。我们将给定的数组 nums 分成 最多 k 个相邻的非空子数组 。 分数 由每个子数组内的平均值的总和构成。
注意我们必须使用 nums 数组中的每一个数进行分组,并且分数不一定需要是整数。
返回我们所能得到的最大 分数 是多少。答案误差在 10-6 内被视为是正确的。示例 1:
输入: nums = [9,1,2,3,9], k = 3
输出: 20.00000
解释:
nums 的最优分组是[9], [1, 2, 3], [9]. 得到的分数是 9 + (1 + 2 + 3) / 3 + 9 = 20.
我们也可以把 nums 分成[9, 1], [2], [3, 9].
这样的分组得到的分数为 5 + 2 + 6 = 13, 但不是最大值.示例 2:
输入: nums = [1,2,3,4,5,6,7], k = 4
输出: 20.50000提示:
1 <= nums.length <= 100
1 <= nums[i] <= 104
1 <= k <= nums.length
方法一:维护前缀和 + 序列DP
class Solution {
public:
double largestSumOfAverages(vector<int>& nums, int k) {
int n = nums.size();
// 前缀和数组
vector<double> sum(n + 5);
for(int i=1; i<=n; i++){
sum[i] = sum[i-1] + nums[i-1];
}
vector<vector<double>> score(n + 10, vector<double>(k + 10));
for(int i=1; i<=n; i++){
for(int j=1; j<=min(i, k); j++){
if(j == 1){
// 分为1份
score[i][1] = sum[i] / i;
}
else{
// 分为多份,递推考虑
// m是指最后一个子数组的起点,取2和j的最大值
// 因为j是当前最少需要的份数
// eg:i=4,j=3 如果此时m=2,没有意义,
// 2如果是最后一个子数组的起点,那么最多只能分为2份
for(int m=max(2, j); m<=i; m++){
score[i][j] = max(score[i][j], score[m-1][j-1] + (sum[i] - sum[m-1]) / (double)(i - m + 1));
}
}
}
}
return score[n][k];
}
};
心得
这道题一开始没注意到 邻近 两个字,因此我一开始的思路是错的 「将数组 nums sort降序排序,前 k-1 个元素各占一份, 后面的元素作为第 k 份」,由于忽略了 『邻近』的条件,这个方法只能通过大约一半的测试点。
方法:前缀和 + 序列DP
题意可以理解为:「将 n 个元素划分为最多 m 个连续段,最大化连续段的平均值之和」。
为了方便,令所有数组的下标从 1 开始。
定义 「 f[i][j] 为考虑将前 i 个元素划分为 j 份的最大平均和 」,答案为 f[n][k] ,其中 1 <= k <= m。接下来考虑 f[i][j] 的计算,由于划分出来的子数组不能是空集,因此可以根据 j 的大小分情况讨论:
- 当 j = 1 时,
- 当 j > 1 时,此时枚举最后一个子数组的起点 k ,其中 2 <= k <= i,此时有平均值之和为:
最终 f[i][j] 为枚举所有k 值的最大值。其中 求解连续段之和可以用 前缀和 进行优化。同时,想要简化代码,还可以利用一个简答的数学结论:「 划分份数越多,平均值之和越大,因此想要取得最大值必然是恰好划分成 m 份」。
![此时 f[i][j] = (∑ nums[inx- 1]) / i;](https://img-blog.csdnimg.cn/25dfd6a53e0642849005d42db2303bd4.png)
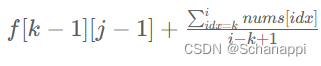






![[附源码]计算机毕业设计SpringbootON-FIT](https://img-blog.csdnimg.cn/58cae32661e247b092622a51e29166e2.png)




![[漏洞复现]Text4shell(CVE-2022-42889)](https://img-blog.csdnimg.cn/576a1bd859f04667a14890d6f1de0f63.png)