一、CT重建基本原理

CT 系统成像基本模型可以描述成：

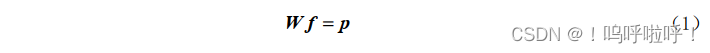
  f为待重建图像，P为投影数据，W为系统矩阵，其中，投影矩阵反映探测器上的投影与重建物体的关系，其模型刻画对于重建速度和精度有着重要影响。

二、投影矩阵模型分类

  投影矩阵的模型刻画一般考虑两个方面：重建物体的离散模型、射线与物体的作用关系；重建物体的离散模型一般是以网格像素（二维图像）或立方体体素（三维图像）的形式进行刻画；而其他的模型主要是以不同的基函数插值的方式进行刻画。常见的射线覆盖模型有点模型、线模型和面积模型等。

1、点模型

  点模型是最简单的系统矩阵模型，该模型认为体素值集中在体素的中心，对于射线穿过体素中心的认为其系统矩阵的值为１，未穿过则为0，也就是说探测器检测的结果是有和无两种：


                 图1 点模型系统矩阵说明图
像素驱动模型常被用来求解基于点模型的投影值，利用的插值方式一般为最邻近插值、线性插值。
模型优点：计算速度快
模型缺点：重建的精度不高，图像有锯齿状伪影
解决方案：
（1）利用 splatting 法对高频信号进行加权处理，但是这会大大增加计算的复杂性；
（2）求解时将像素分解成多个子像素，提高投影图像的分辨率。

2、线模型

  线模型系统矩阵是目前迭代重建算法中最常用的模型。线模型中射线与图像像素（体素）相交的长度代表射线穿过的像素的权重值。探测器检测结果为射线方向的累积值，并认为射线没有宽度。

                  图2 线模型系统矩阵说明图
  常用的基于线模型的投影矩阵系数的计算方法有两种：
① 计算射线与像素之间的交线长度；
② 通过插值的方法。
  线模型通常是利用射线驱动方式计算矩阵系数，即第一种方式----用射线与像素之间的交线长度作为权重系数。
（1）Siddon’s算法
  最常用的是 Siddon 所提出的逐行求交点，再用交点进行排序计算交线长度的方法。后又对其进行改进，免于排序过程，提高了计算效率（siddon算法）；
（2）Joseph算法
  除此以外，插值法也是射线驱动常使用的方法，插值有很多种， 最常用的是 Joseph所提出的线性插值法（Joseph算法），还有Wang 提出的等距采样插值法；
（3）计算线积分的简单方法
  Kohler, Turbell, and Grass (2000)等人提出了一种计算线积分的简单算法（原理类似等距采样法）；这种简单算法利用三线性插值，通过连续体积的积分近似于沿射线等距点的值相加。步宽h是一个自由参数，可以用来权衡图像质量和计算时间。N表示过采样因子，N = 1对应的采样距离等于体素采样距离。原理如图所示，似乎与等距采样类似（待查阅资料证实？？？）。


（4）K¨ ohler’s算法
  该算法利用辛普森积分规则在每个单元内解析计算线积分的值。算法基本结构为：
1:for 对于每一个被射线相交的体素
2:用双线性插值法计算体素边界两个交点处的函数值
3:用三线性插值法计算上述两个交点中间点的函数值
4:用辛普森法则将三个值合并
5:累积结果
6:结束
PS：辛普森法则


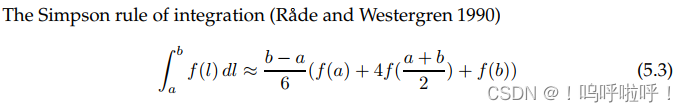
（5）距离驱动DDM算法
  2004 年，De Man 结合了像素驱动和射线驱动优点，提出了距离驱动模型，并被认为是线模型中效果最好的方法；
（6）分离足迹的距离驱动算法（splatting算法？？）
  而在三维投影模型中，投影值会在光源的方位角为 π/4 时产生最大的误差，因此2010 年 Fessler 提出了分离足印函数（Separable Footprints，SF）的方法改善这种情况，方法中，体素的足印函数被近似为两个二维足印函数的乘积（这也是现在一般应用的距离驱动进行三维投影模拟时使用的方法，DDM算法）；除此以外，2013 年，Chuang对距离驱动模型进行了改进，提出了一种将探测器边界投到像素的两条边界的方法（改进的距离驱动算法）。

3、面模型

  面积模型的提出则避免了插值的过程，近似真实投影模型中射线从理想光源到理想探测器中的积分，有效地保持了重建精度。
  二维的面积模型中，探测器的采样点被看成是一条线段，穿过的射线是具有宽度的射线。在实际计算中，求解面积的计算量较大。一种简化的方法是将射线看作光源投射到探元的多条线的集合，并通过计算各条线权重系数的平均值进行求解，该方式称为带状积分模型。

                 图3 面模型-带状积分模型示意图

其中，S 代表穿过的射线条数。
  De Man提到直接求射线和，但会因为部分像素具有非线性的属性带来误差。他对公式 进行了修正，证明可以有效避免投影因误差产生的伪影。
  Yu 提出了区域积分模型，该模型是通过计算每一个像素与每一条射线之间相交区域积分以及标准化因子，来得到每一个像素对于投影的贡献。标准化因子通过像素中心点到光源的距离以及射线源与探元连接的夹角计算得到。该模型优点为：降低由于探元和像素尺寸因素在正反投影计算中带来的误差。

面模型优点：（1）不论像素和探测器单元的尺寸大小（2）面积模型对于正反投影都适用（3）面积模型的成像质量较好；
面模型缺点：（1）计算量很大（2）而且仅限于在二维重建中计算系统矩阵，无法扩展到三维情况，限制了其在实际中的应用。

4、基函数模型的投影矩阵

  前面叙述的投影矩阵的建立方法都是选用内部均匀的网格或者立方体单元来表示重建区域的离散结构。但实际上，物质的分布可能是不均匀的。为了刻画物质内部不均匀性，可以选用不同的基函数通过插值的方式来减少误差。
  基函数模型根据构造方式的不同有很多，例如立方体模型、傅里叶级数模型、小波模型、球体（或圆盘）重叠模型、Kaiser-Bessel 窗函数模型、自然像素模型、B-splines模型、狄拉克冲激函数模型和高斯函数模型等等。
  Kaiser-Bessel 窗函数模型（blobs） 是一种采用比较普遍的具有轴向对称性的基函数模型，能够克服边缘伪影和混淆现象，其在 X 射线成像和正电子发射型成像中起到了较好的效果。

相关文献：
[1] Forward and backprojection model(FP/BP)

5、正反投影矩阵选择

  一般来说，正投影的计算适合用射线驱动，即以探元索引为线程编号；而反投影的计算适合用像素驱动，即以像素索引为线程编号。如果要用同一种驱动方式，则在并行计算过程中会产生对访存进行“写操作”的冲突。

参考文献：
[1] An improved algorithm for reprojecting rays through pixel images [Joseph, IEEE TMI, 1982]
[2] Splatting Algorithm Apply to Algebraic Arithmetic of Three Dimensional Computer Tomography
[3] Siddon RL. Fast calculation of the exact radiological path for a three-dimensional CT array[J]. Medical Physics, 1985, 12(2): 252-255.
[4] Distance-driven projection and backprojection[R]. IEEE Nuclear Science Symposium and Medical Imaging Conference
[5] Distance-driven projection and backprojection in three dimensions
[6] CT重建中投影矩阵模型研究综述_陈建林