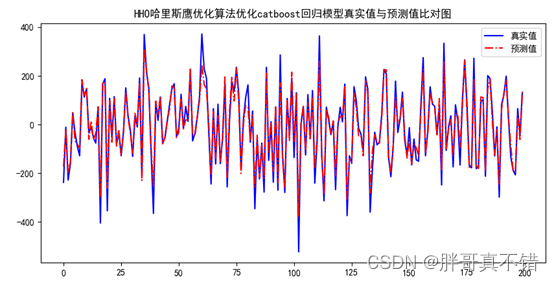
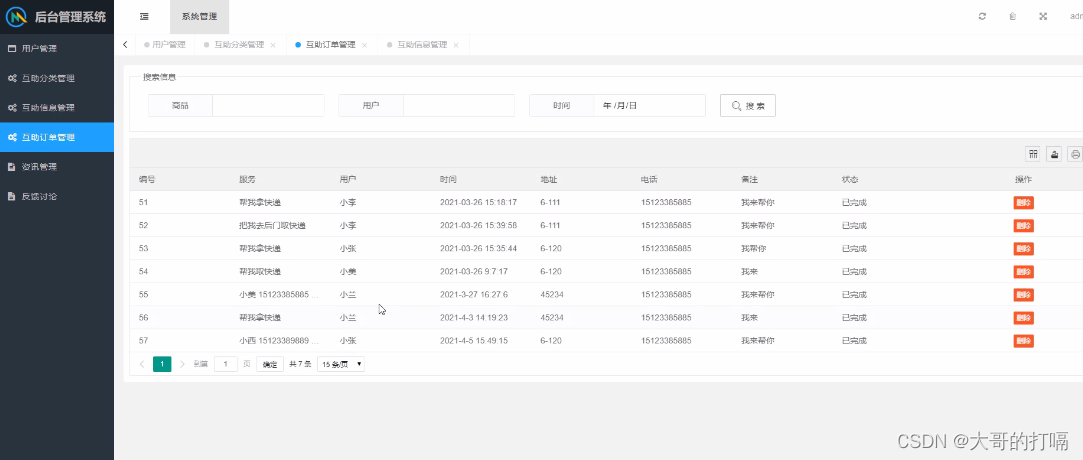
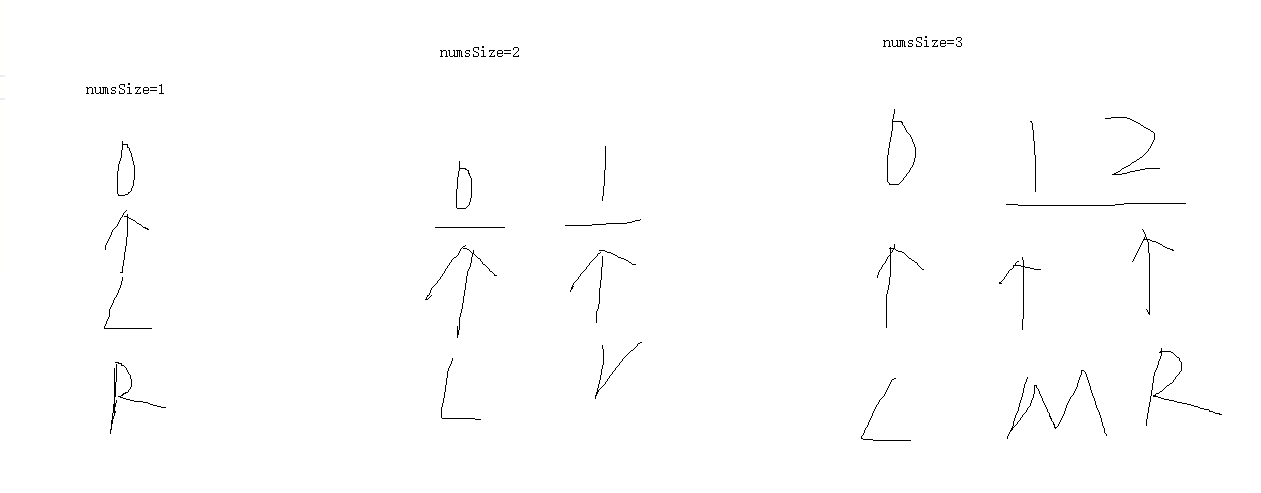​《Protein Actions Principles and Modeling》-《蛋白质作用原理和建模》

本人能力有限，如果错误欢迎批评指正。

第六章：The principles of protein folding kinetics

（蛋白质折叠动力学的原理）

-速率测量有助于深入了解蛋白质折叠的途径

可折叠的路线是什么？在折叠过程中什么时候形成不同的结构？不同的实验探头会报告不同的信息。假设你有两个探针，一个报告螺旋形成，另一个报告链坍塌。原则上，在一个蛋白质的折叠实验中，观察两个探针的时间依赖性可以告诉你该蛋白质的折叠和螺旋形成事件的相对顺序。但这种实验是一个比较大的挑战。因为被研究的小蛋白质折叠过程通常是双态的；换句话说它们只用一个动力学相来折叠。因此，在没有其他信息的情况下，关于双态折叠的蛋白，我们只能说：“一切都发生在一个动态事件中。”如果想形成一个关于折叠路径的更详细的叙述，我们需要独立的信息或者多状态折叠蛋白，此时，我们可以描述动力学中间状态。

图6.6 不同的可能存在的折叠路径。从变性状态（左侧无序）到自然状态（右侧螺旋）的不同动力学路径。(A)双状态进程：它同时发生。(B)首先，螺旋1形成，它作为一个模板，协助螺旋2的形成。(C)螺旋1独立于螺旋2形成，然后它们聚在一起。

图6.6显示了三种假设的折叠路径。在一种情况中，折叠作为单一事件发生。另一种情况是，两个螺旋大约在同一时间分别形成，然后这两个完全形成的螺旋连接在一起。第三种情况是首先形成一个螺旋，提供第二螺旋的表面。此外，还有别的一些折叠路径假设。对折叠机制的研究已经推动了也促进了相关实验的研究，一些具体的内容会在本章进行展示。

一个研究充分的动力学中间态涉及脯氨酸异构化(proline isomerization)。脯氨酸可以在两种不同的异构态之间相互转换，即顺式和反式肽键。在天然结构中，脯氨酸的相互转换速度较慢。在变性蛋白中，脯氨酸将处于两种异构体态之间的玻尔兹曼平衡状态。在折叠时，每一种蛋白质的非天然脯氨酸必须转化为脯氨酸的天然状态的异构体。所以，折叠有两个动力学阶段。在慢速阶段，蛋白质从错误的脯氨酸异构体开始。这种折叠是缓慢的，因为脯氨酸的异构化速度很慢。

在牛胰蛋白酶抑制蛋白（BPTI）的折叠中发现了另一种动力学中间体，它的天然结构在6个半胱氨酸之间有3个二硫键。有趣的是，BPTI中的二硫键并不是在自然慢慢形成的。在快速阶段，蛋白质的构象已经处于正确的异构状态。一些错误的二硫键首先瞬间形成，然后它们被解开，然后最终形成正确的二硫键。这些不正确的二硫化物被称为路径上的错误折叠态( on-pathway misfolded states)。

其他蛋白质也可以在其折叠路径上通过非天然状态。如图6.1A所示的溶菌酶折叠动力学为单一指数。然而，通过多种方法，已经表明溶菌酶的两个结构域在折叠过程中表现有所不同。α域折叠迅速。一旦α域形成，β域就会折叠。该蛋白在快速过程中过快，表明螺旋的形成可能走得太远，从而形成一些非天然的残基接触，然后会在较慢的β-折叠形成步骤中纠正。因此，溶菌酶似乎涉及复杂的多种途径。β-乳球蛋白也具有多相动力学的折叠。β-乳球蛋白是一个β-桶由9个反平行的β链，一个主要的α-螺旋，和4个短螺旋。在折叠过程中，分子首先形成β-螺旋结构，然后采用天然状态的α-桶结构。

突变研究可以探测折叠途径

我们可以通过研究突变的蛋白质来深入了解折叠的路线。一种叫做Φ值分析的方法提供了关于蛋白质的一些信息，它可以告诉我们蛋白质折叠过程中哪些部分折叠缓慢，哪些部分折叠更快。在Φ值分析中，蛋白质一次突变一个氨基酸。我们测量了野生型蛋白的折叠速率系数kf,wt和突变体的折叠速率系数kf,mut。公式式6.17表明，由突变引起的过渡态势垒自由能的变化将为：

要进行Φ值分析，还必须测量由突变引起的蛋白质稳定性ΔGf的变化，或者等价地测量突变体kf,mu相对于野生型kf,wt的平衡常数的变化。然后Φ值则为：

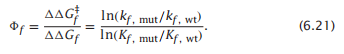
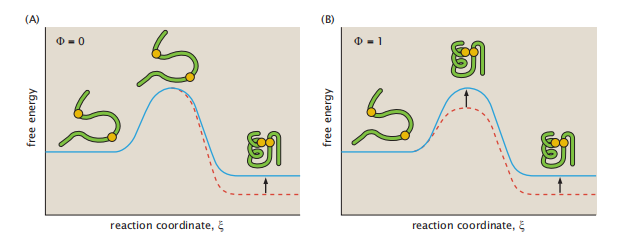
图6.7 Φ值通常用过渡状态的结构来解释。(A)Φ=0表示突变位点在处于过渡状态时具有变性样结构。(B)Φ=1表示突变位点在处于过渡状态时具有天然结构。蓝色实心曲线为野生型，红色虚线曲线为突变型。

Φ值通常处于0到1的范围。图6.7显示了Φ值。Φf = 0意味着突变对折叠速率没有影响。观察Φf = 1意味着突变对折叠自由能垒的影响和影响折叠稳定性一样大。所以突变结果都会如下解释。当Φf = 0的时候，意味着当氨基酸链其他部分已经通过了过渡状态但是突变氨基酸还没形成折叠结构，而Φf =1的时候意味着当氨基酸全部完成折叠过渡态的时候这个突变氨基酸也是处于天然结构中的。

如果在多个位点上发现非零的Φ>0，那么过渡态被称为扩散，这意味着蛋白质中许多不同的氨基酸参与控制折叠速率。相反，如果在整个蛋白质中发现Φ≈0，那么过渡状态被称为极化，这意味着只有蛋白质的少数氨基酸控制着折叠速率。例如，糜蛋白酶抑制剂2具有扩散性过渡态，泛素具有极化过渡态。

变性剂可以改变折叠率：Chevron 图

图6.8 Chevron 图显示了变性剂如何影响折叠动力学。左边的直线表明，降低变性剂浓度的速度会加速折叠。右边的直线显示变性剂加速展开速度。cm是变性的中点。将谱线外推到零变性剂上，得到了水中的折叠和展开速率系数kf和ku。这里显示的例子是酰基辅酶a结合蛋白。

加入变性剂，如盐酸胍（GuHCl）或尿素，可以减缓折叠和加速展开。变性剂对折叠率系数的影响用Chevron 图表示。Chevron 图显示了在纵轴上观察到的弛豫速率与在横轴上的变性剂浓度的对数的关系（图6.8）。术语chevron指的是图的V形（如果绘制折叠时间的对数，则为倒对数形）。V的左分支描述了当系统跳到低变性剂浓度时你看到的折叠速率，展现了折叠过程。V的右分支描述了跳跃到高变性剂浓度，展现了结构展开的过程。对于具有双态动力学折叠的蛋白质，折叠和展开速率系数的对数是变性剂浓度的线性函数（见图6.8）：

mf < 0和mu > 0，被称为动力学m值，是这两条线的斜率。添加变性剂可以减缓蛋白质的折叠，加速蛋白质的展开。在Chevron 图中，速率系数与变性剂浓度的对数的线性行为类似于蛋白质稳定性的平衡常数（m值）的线性关系（见第3章）。k0 f和k0u分别是在无变性剂的情况下的折叠速率和展开速率。对于服从双态折叠/展开动力学的蛋白质，我们可以将平衡展开自由能ΔGu=-ΔGf与折叠和展开的速率系数联系起来：

在变性中点（即图6.8中的cm处），我们会发现kf = ku。

为什么Chevron是v形的？从方程6.9中回想一下，观察到的弛豫速率系数是折叠和展开的速率系数之和kobs=kf + ku。在低变性剂浓度下，蛋白质是天然的，ku很小，所以kobs≈kf，因此左边主要体现折叠过程。在高变性剂浓度下，蛋白质变性，kf很小，所以kobs≈ku（见图6.8）。因此，当绘制kobs与变性剂浓度的对数时，我们会得到两条直线，给出一个像字母v这样的形状。

图6.9 添加盐可以加速蛋白质的折叠并且减慢其展开。在没有（蓝色）和存在硫酸钠（红色）的情况下，Chevron图绘制了核糖体蛋白S6的折叠。rollover（红色）表示在低变性剂浓度下，折叠达到了最大速度。盐能稳定天然蛋白质。

v形图表明一个蛋白质具有双态折叠动力学。当折叠比单一指数更复杂时，Chevron图不是v形的。图6.9显示了一个Chevron图的 rollover。其中Chevron图的一个臂是弯曲的或形成一个平台，而不是一条直线。rollover的Chevron图表示了折叠中间体或动力学陷阱的存在：进一步加强折叠条件（从Chevron图的x轴上向左移动）并不会加速蛋白质折叠速度。Chevron图的翻转意味着一个更强的外部力量不能克服蛋白质的某些内部速度限制。

我们也可以将突变与Chevron图相结合。要做到这一点，首先要测量一系列不同变性剂中蛋白质的折叠和展开速率，为野生型蛋白质绘制一个Chevron图。然后在蛋白质中特定的氨基酸位点发生突变。现在为突变蛋白做另一个Chevron图。在同一界面上绘制两个线形图。6.10显示了两个极限情况:(A)在一个情况中，突变改变了Chevron图的折叠臂，但没有改变展开臂。这表明该突变位点有助于控制折叠速率。(B)在另一种情况下，突变改变了展开臂，但没有改变折叠臂。这表明突变位点对折叠没有速率控制。

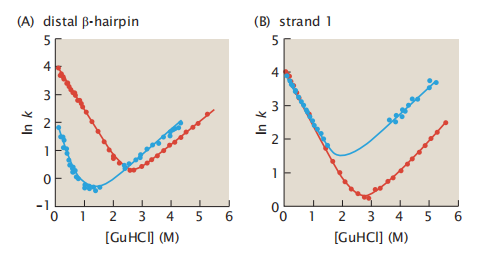
图6.10 一些突变改变了折叠速率，有些突变改变了展开速率。(A)SRC激酶SH3结构域的“远端”β-发夹的突变只改变了Chevron图的折叠臂。(B)第一个β链的突变只改变了展开臂。野生型为红色，突变型为蓝色。

在双态蛋白质研究中，Chevron图给出了一个信息：主要的折叠机制（最慢的步骤）独立于蛋白质的起始状态。Chevron图的折叠臂完全由蛋白质所在的溶液态决定。折叠臂并不依赖于蛋白质在转变前的初始状态。我们可以从高度变性的条件下开始折叠过程，这个时候蛋白质几乎没有部分折叠的结构。或者我们可以从弱变性条件下开始折叠过程，这个时候蛋白质可能有相当大的部分折叠结构。这并不重要。最慢的弛豫时间并不随不同初始条件的变化而变化。

-------------------------------------------

欢迎点赞收藏转发！

下次见！