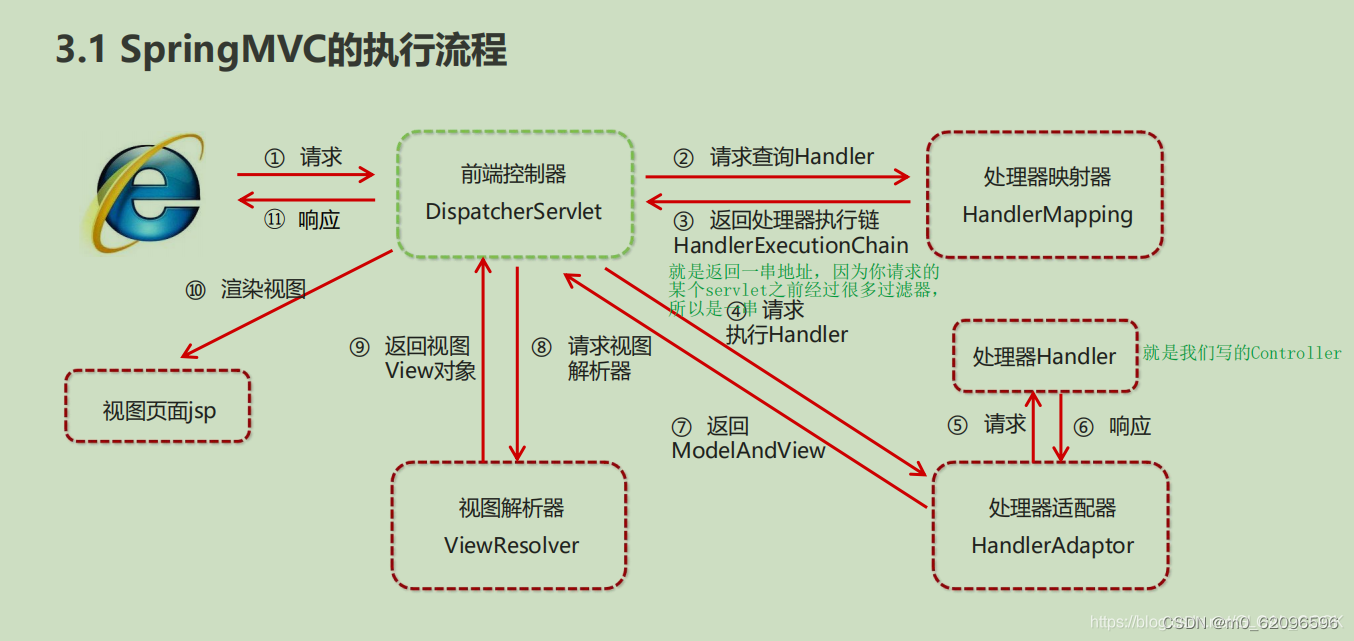
一,定义
欧拉函数是对于n小于或者等于他的数中与n互质的数的个数。一般用φ(x)表示。
二,欧拉函数公式
其中pi为n的所有质因数。
公式的理解方法可以是pi是与n互质的数,那么它(包括它的倍数)在1~n里面是均匀出现的,概率为1/pi,显然这1/pi的数都与n互质,先筛去,剩下n*(1-1/pi)的数,同理对于pj,剩下的数里面有1/pj的数是与n不互质,再筛去1/pj,剩下n*(1-1/pi)*(1-1/pj).......当我们把所有质因数的倍数筛去,剩下的就是与n互质的数。
三,欧拉函数的性质
-
若p为质数,φ(p)=p-1
这个显然1~p-1都与p互质,除了p。 -
若p为质数,对于p^k,有φ(p^k)=p^k-p^(k-1)
在范围内,与p^k不互质的数,显然与p^k的gcd是p,那么只要那个数可以*p并且不超过范围,这个*p后的数与n^p不互质,显然1~p^(k-1)都可以*p不超过范围,那么就有p^(k-1)个数与p^k不互质. -
当n>2是,与n互质的数总是成对存在,如gcd(a,n)=1,则gcd(n-a,n)=1。
我们假设gcd(n-a,n)=m(m!=1),则有n=p*m,n-a=q*m,那么有a=(p-q)*m,则有a与n有公约数m,与gcd(n,a)=1矛盾,得证。 -
因此,n>2时,φ(n)是偶数,而且小于等于n的数中,与n互质的数的总和为:φ(n) * n / 2 (n>1即可)。
每一对和为n. -
我们可以把n写为其分母形式的数有,1/n,2/n,3/n...n/n。将他们化简会发现,分母都是n的因数(包括1和它自己),而分子则是分母自己的欧拉函数中的数(小于等于分母且与分母互质的数),这些对,刚刚好就是n对,即所有n的因数的欧拉函数和就是n(个)。,即n的因数(包括1和它自己)的欧拉函数之和等于n。
-
欧拉函数是积性函数
- 首先积性函数定义:如果函数f:N->R,满足对于任意一对互质的正整数p,q,都有f(pq)=f(p)*f(q),则称f为积性函数。
- 证明欧拉函数是积性函数:gcd(n,m)=1,φ(n)=n*(1-1/p1)*(1-1/p2)....φ(m)=m*(1-1/q1)*(1-1/q2)....,φ(n)*φ(m)=n*m*(1-1/p1)*(1-1/q1).....(因为n与m互质,显然他们的质因子也都是互质的,那么p与q不重复),显然等于φ(n*m)。
- 特殊的,当n是奇数时,φ(2*n)=φ(n)

四,求欧拉函数
1,求单个欧拉函数,根据定义即可,我们每次筛出其质因子,就*(1-1/pi)
int phi(int n)
{
int ans=n;//初始取n,后面不断乘分式
for(int i=2; i*i<=n; ++i)
{
if(n%i==0)
{
ans=ans/i*(i-1);
while(n%i==0)n/=i;
}
}
if(n>1)ans=ans/n*(n-1);
return ans;
}2,求1~n所有欧拉函数,我们可以利用积性函数的性质使用欧拉筛实现O(n)求出
const int N = 2e5 + 10;
bool vis[N];
int ou[N],phi[N];//ou[]为线性筛出的质数,phi为欧拉函数
void euler_phi(int n)
{
vis[1]=1,phi[1]=1;
for(int i=2; i<=n; ++i)
{
if(!vis[i])
{
ou[++ou[0]]=i;
phi[i]=i-1;//质数的欧拉函数
}
for(int j=1; j<=ou[0]&&i*ou[j]<=n; ++j)
{
vis[ou[j]*i]=1;
if(i%ou[j]==0)//如果ou[j]是i的最小质数,那么显然不互质了,不能用积性函数求欧拉函数。
{
//但是,我们还有定义,根据定义,我们phi[ou[j]*i]=ou[j]*i*(所有质因子那串),发现i包括了所有质因子,说明原式可以化为ou[j]*phi[i]
phi[ou[j]*i]=phi[i]*ou[j];
break;
}
phi[ou[j]*i]=phi[i]*phi[ou[j]];//i与ou[j]互质用积性函数性质求欧拉函数
}
}
}