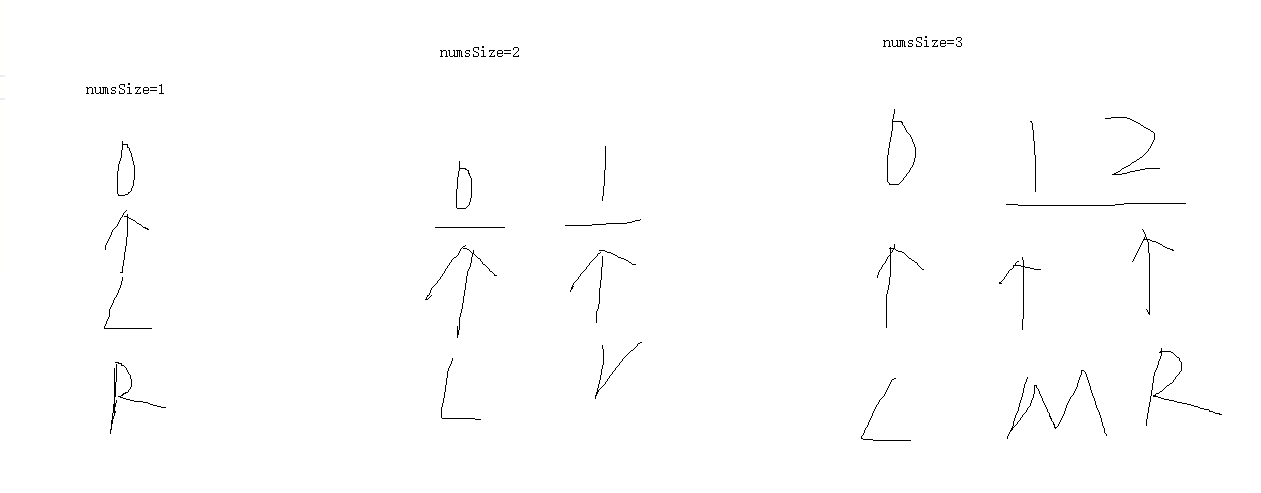高级数据结构与算法 | 基数树（Radix Tree）

news2024/11/25 15:33:11

文章目录

  • RadixTree
    • 基本概念
      • 概念
      • Radix Tree VS Trie Tree
      • 应用场景
    • 实现
      • 数据结构
      • 插入
      • 删除
      • 查找
      • 完整代码

RadixTree

基本概念

概念

如果对 Trie 不太了解，可以看看我的往期博客：

https://oreki.blog.csdn.net/article/details/109076473

Radix Tree是一种基于 Trie（字典树）的数据结构，旨在解决字符串搜索和匹配的问题。它最早由 Fredkin 在 1960 年提出，并在之后被广泛应用于各种应用领域。其最大的特点就是在 Trie 的基础上，加入了路径压缩的逻辑，通过合并前缀的方式大大的减少了 Trie 中的节点冗余问题，不仅提高了查询效率，还减少了存储空间的使用。

Radix Tree VS Trie Tree

那么，Radix Tree 是如何做到合并前缀的呢？在 Radix Tree 中每个节点存储的不再是一个字符，而是字符串的前缀，当插入/删除节点时，会通过合并/分裂前缀的方式，来尽可能的压缩树的高度，下面给出几个例子来进行对比。

下面来分别对比一下在 Radix/Trie 中，插入和删除的流程

插入：

初始状态

image-20230402233052316

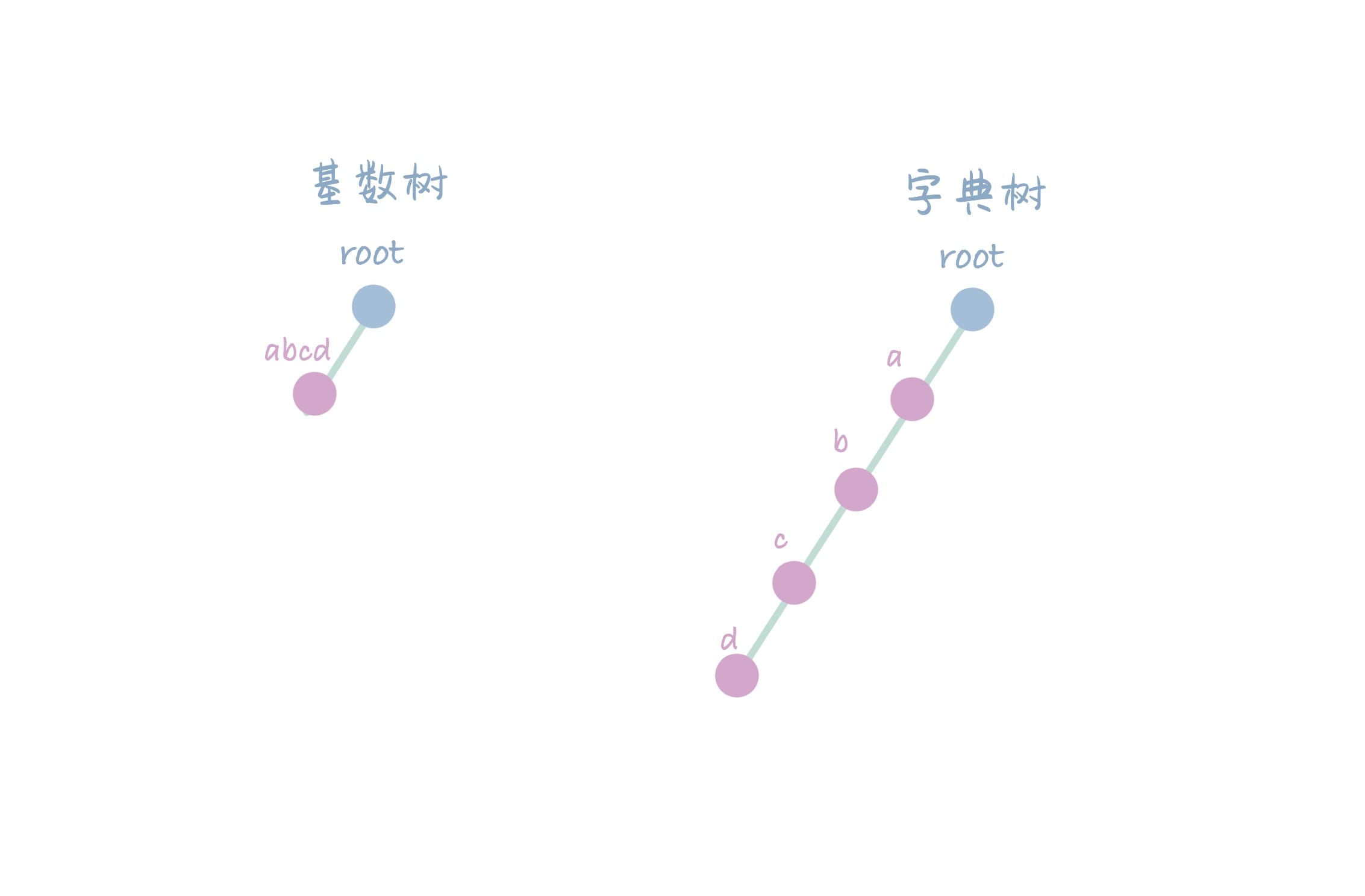
初始状态

插入 abcd，此时 Radix Tree 会将前缀保存到同一个节点中。而 Trie 一个节点只能保存一个字符。

img

插入 abcd

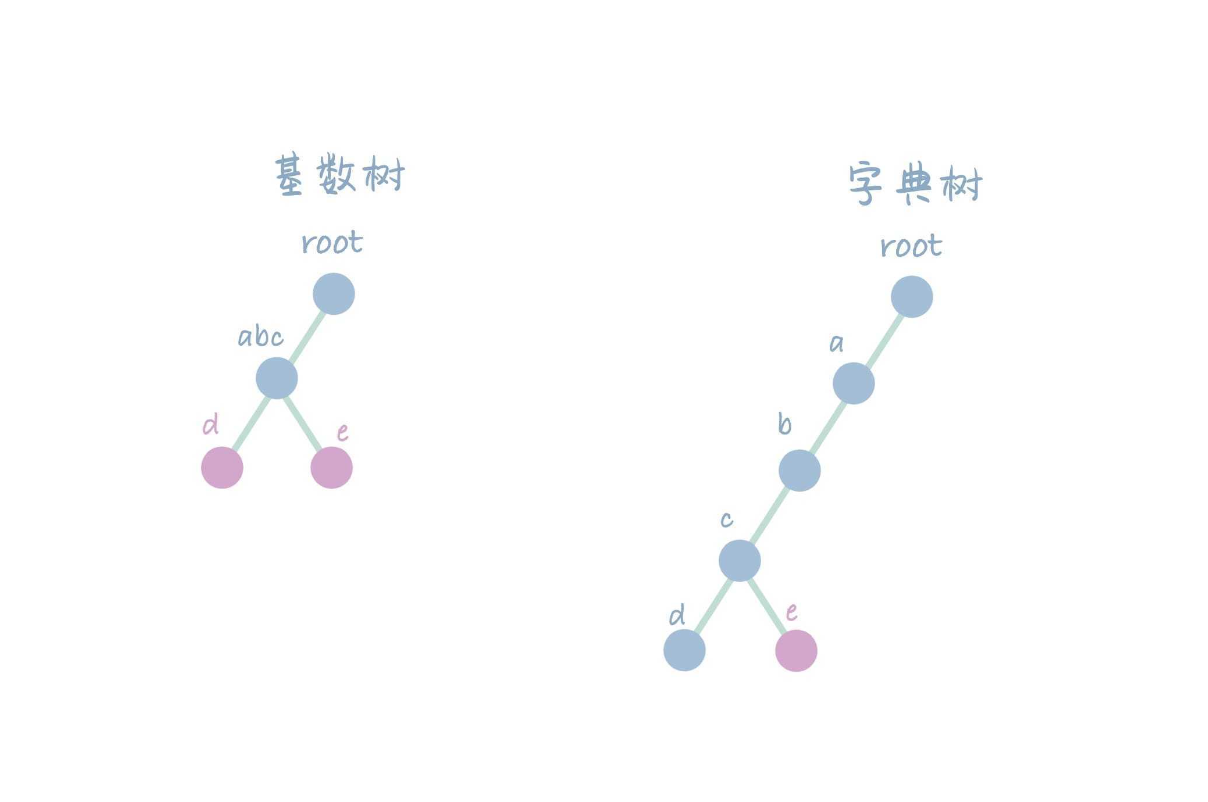
接着插入 abce，此时 Radix Tree 会获取找到匹配到最大前缀的节点 abcd，保留最大前缀，并将 d 和新插入的 e 存储到子节点中。

image-20230402233226662

插入 abce

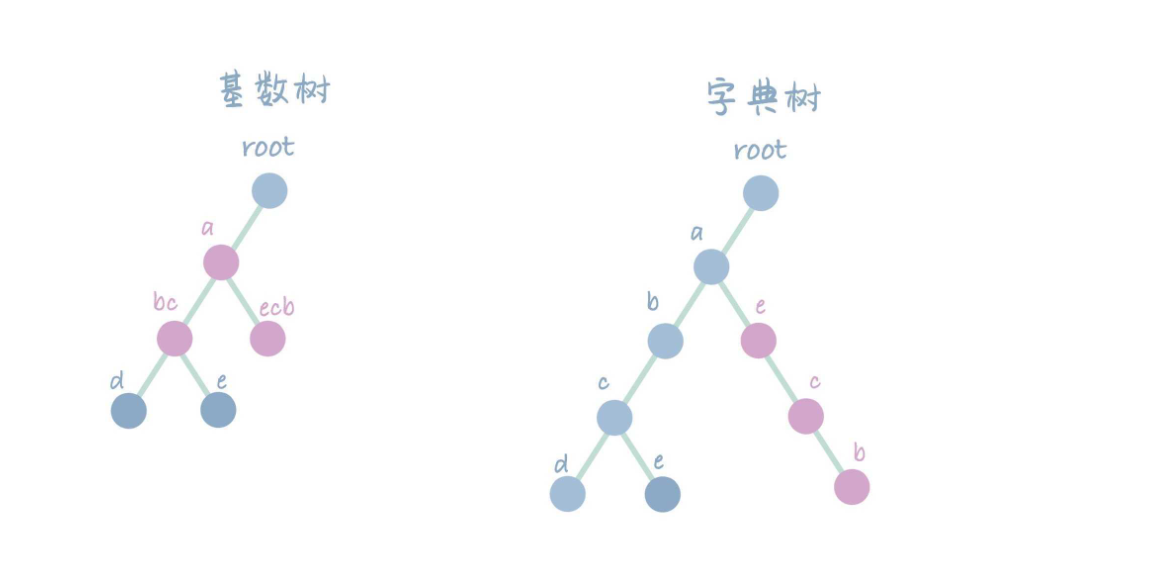
接着插入字符串 aecb。此时找到具有最大前缀的节点 abc，将其拆分为前缀 a，后缀 bc，将 bc 作为 a 的子节点，并继承其原有子节点，同时将新插入的字符串 ecb 存储到 a 的子节点中。

image-20230402233330307

插入 aecb

插入 aecd，此时找到最大前缀节点 ecb，保留匹配前缀 ec，将剩余字符 b 和新插入节点 d 作为子节点。

img

插入 aecd

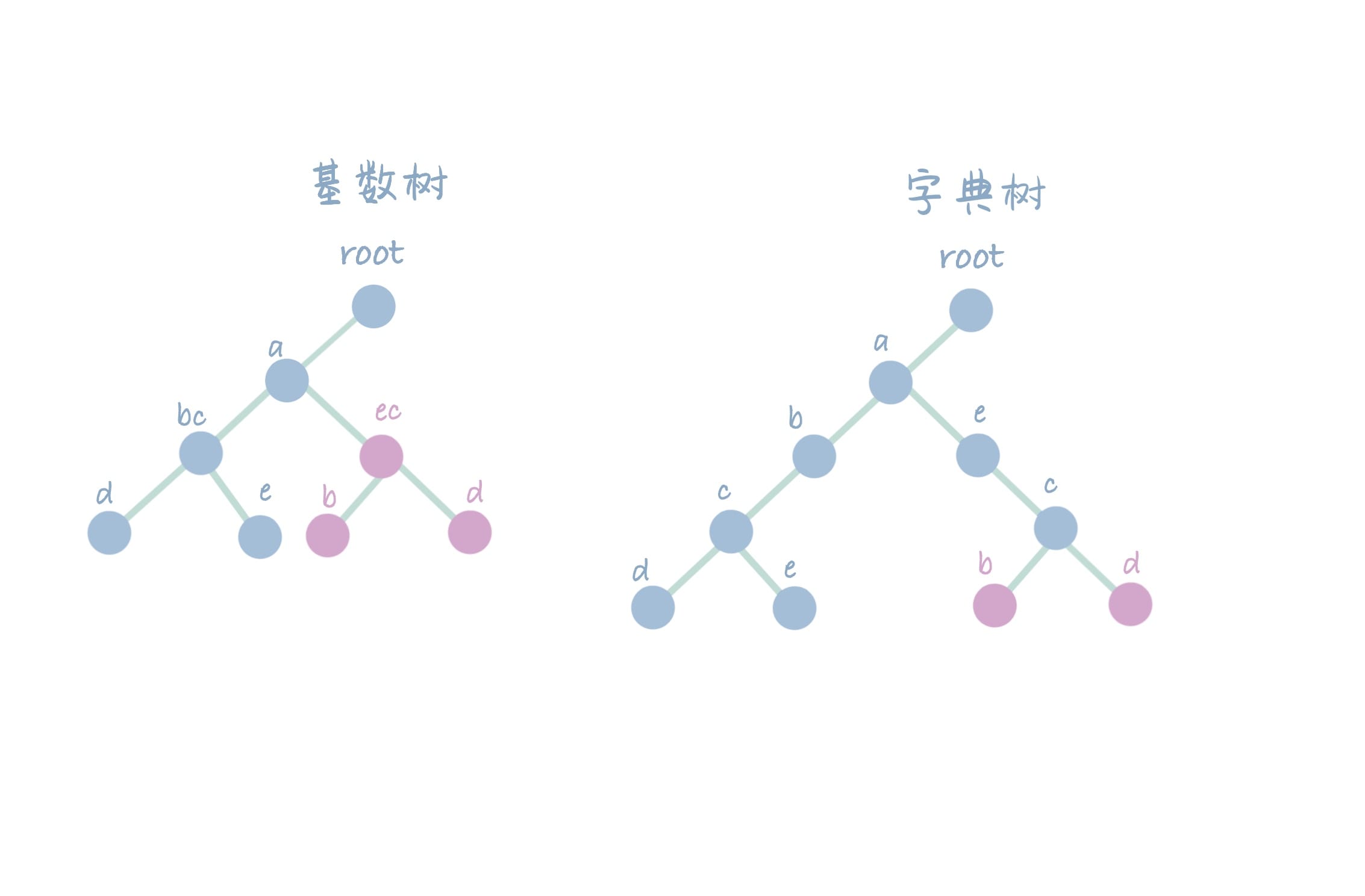
删除：

基于上面的树，接着进行删除，首先删除 abcd。此时由于 d 被删除，整下 bc 和 e 节点为单路径，此时将其合并为 bce。

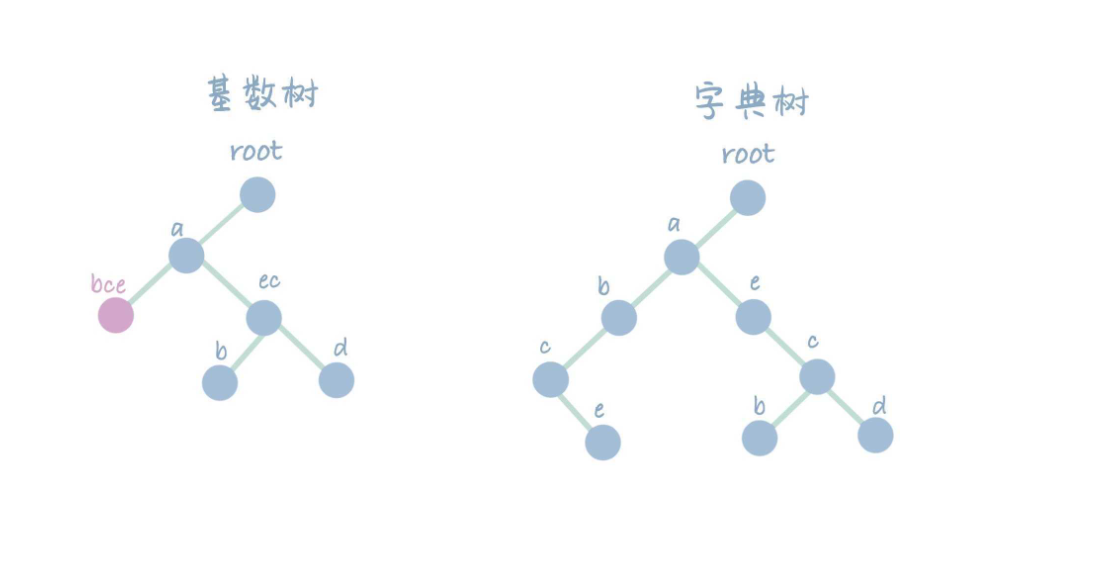
image-20230402233550741

删除 abcd

删除 abce，同理，此时 a 仅剩下单路径，将其与 ec 合并为 aec。

img

删除 abce

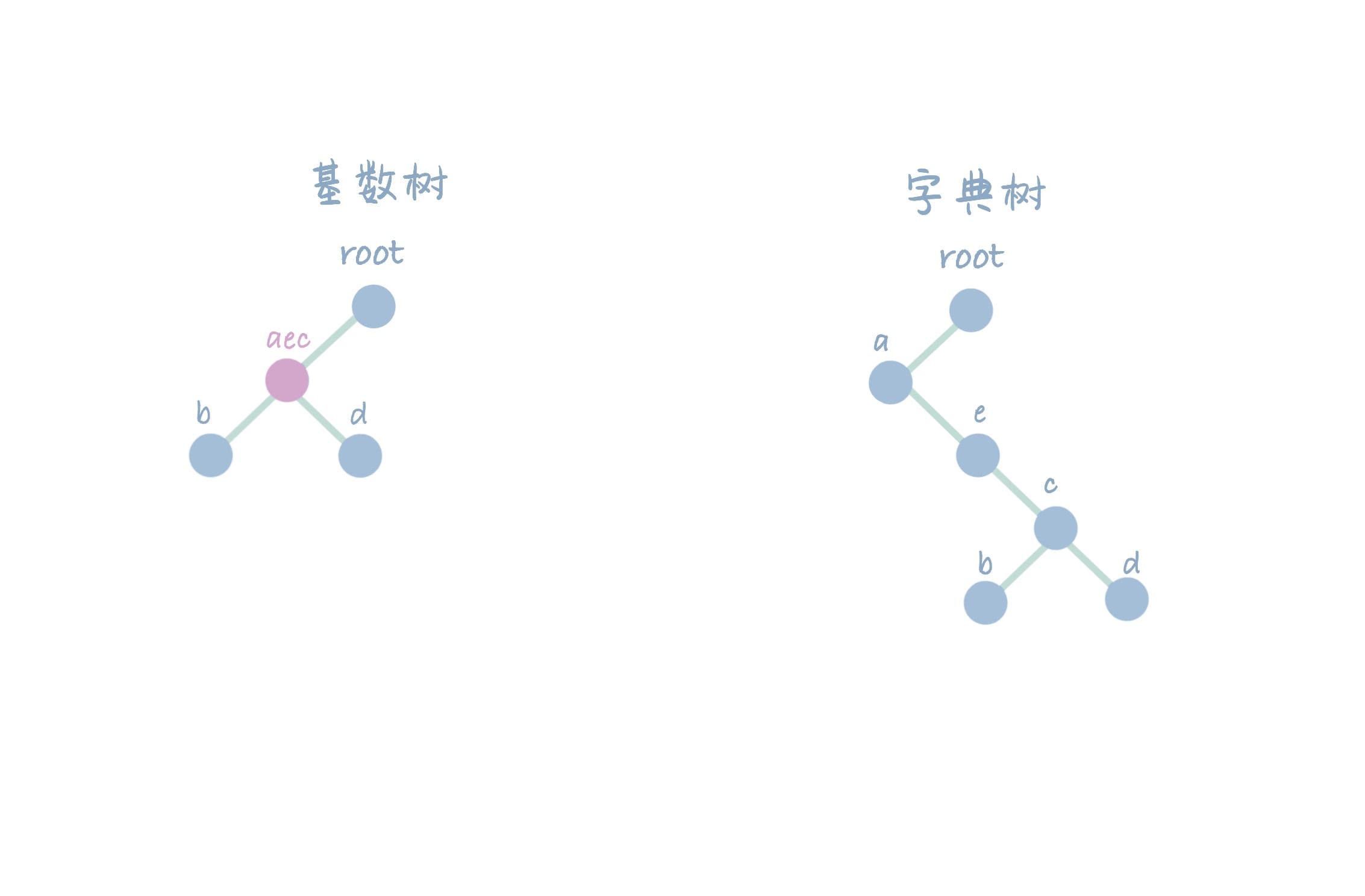
删除 aecb，合并 aec 与剩余路径 d，变为 aecd。

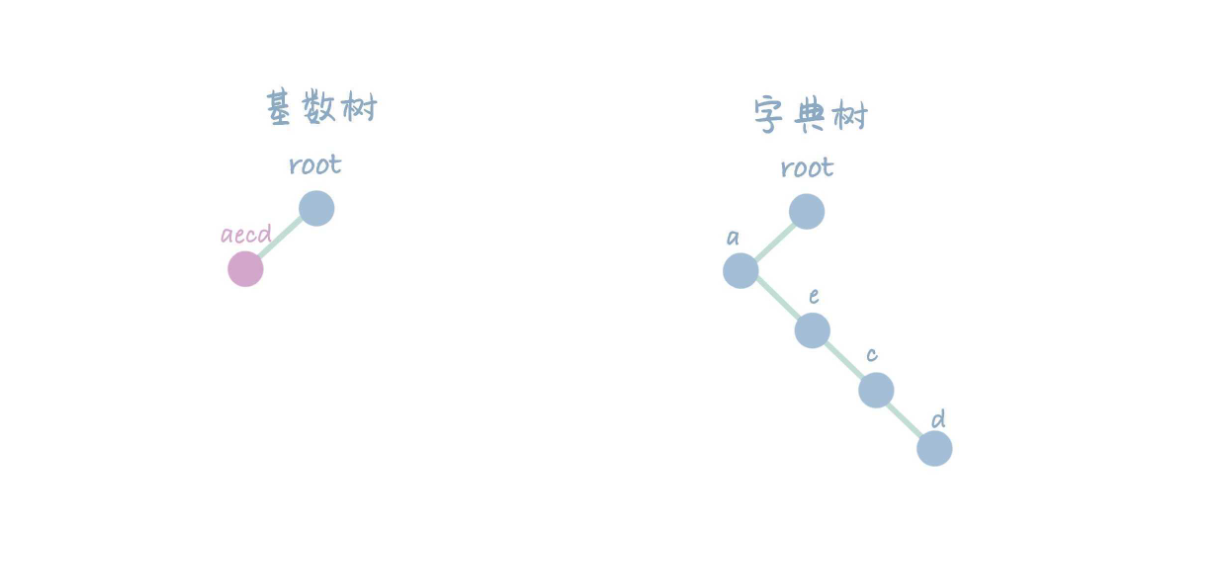
image-20230402233928027

删除 aecb

接着删除 aecd，此时两树为空。

image-20230402233915793

删除 aecd

应用场景

由于 RadixTree 具有高效的字符串匹配能力以及空间效率，其被广泛应用于字符串搜索、匹配的场景，比较常见的几个用法如：

  • 路由表、DNS 等网络设备的查找和匹配。
  • 编译器中预定义符号和关键词查找。
  • Linux 的进程、线程管理，Page Cache 的搜索。
  • 自然语言处理

实现

上面介绍了原理，下面用 C++ 来简单实现一个 Radix Tree 的 demo。

数据结构

首先定义 RadixTreeNode，我们需要用一个 string 来存储字符串前缀，用一个 bool 变量来标识当前路径是否构成一个完整的字符串，再用一个哈希表来存储所有的子节点（这里不用数组的原因是删除一个节点时，需要偏移多个节点，且查找时需要遍历数组）。

class RadixTreeNode {
public:
  explicit RadixTreeNode(const string &word = "", bool is_end = false)
      : word(word), is_end(is_end) {}

  unordered_set<shared_ptr<RadixTreeNode>> children;
  string word;
  bool is_end;
};

接着定义 RadixTree，首先我们需要存储一个 root 节点的指针，由于 C++ 中没有 GC 机制，为了避免内存泄漏，这里统一用智能指针来进行管理。这里实现了基本的插入、删除、查找函数，以及递归调用的辅助函数。

class RadixTree {
public:
  RadixTree() : root(make_shared<RadixTreeNode>()){};

  virtual ~RadixTree() = default;

  RadixTree(const RadixTree &) = delete;
  RadixTree &operator=(const RadixTree &) = delete;

  void insert(const string &str);

  void erase(const string &str);

  bool search(const string &str);

private:
  shared_ptr<RadixTreeNode> root;
  
  void insert_helper(const string &str, shared_ptr<RadixTreeNode> node);
  
  shared_ptr<RadixTreeNode> erase_helper(const string &str,
                                         shared_ptr<RadixTreeNode> node);
                                         
  bool search_helper(const string &str, shared_ptr<RadixTreeNode> node);

插入

  1. 如果插入的是空字符串，则直接将根节点标记为完整字符串，否则继续往下。
  2. 遍历当前节点的子节点，共有以下三种情况：
    • 节点没有子节点：将字符串的内容直接作为新的子节点插入。
    • 子节点中有能够匹配到前缀的节点：
      • 当前节点的内容与字符串完全匹配：将当前前缀标记为完整字符串。
      • 当前节点的内容是字符串的前缀：此时将字符串拆分为公共前缀和剩余字符，用剩余字符与该子节点继续递归进行查找，寻找合适的插入位置，继续回到流程 2。
      • 当前节点的内容和字符串具有公共前缀：此时将当前节点的内容拆分为公共前缀，剩余后缀两部分。当前节点保留前缀内容，将后缀作为子节点插入，此时如果字符串还有剩余字符，则将其也作为子节点一同插入。
    • 子节点中没有与之具有公共前缀的节点：将字符串的内容直接作为新的子节点插入。
void insert(const string &str) {
  if (str.empty()) {
    root->is_end = true;
  } else {
    insert_helper(str, root);
  }
}

void insert_helper(const string &str, shared_ptr<RadixTreeNode> node) {
  // 如果当前没有子节点，则直接作为新的子节点
  if (node->children.empty()) {
    auto new_node = make_shared<RadixTreeNode>(str, true);
    node->children.insert(new_node);
    return;
  }

  bool is_match = false;
  for (auto current : node->children) {
    int i = 0;
    for (; i < str.size() && i < current->word.size(); i++) {
      if (str[i] != current->word[i]) {
        break;
      }
    }
    if (i != 0) {
      is_match = true;
      // 情况一：当前节点的内容与字符串完全匹配，则直接将该前缀标记为完整
      if (i == str.size() && i == current->word.size()) {
        current->is_end = true;
      } else if (i != current->word.size()) {
        // 如果当前节点的内容是字符串的部分前缀，则进行分裂
        auto new_node = make_shared<RadixTreeNode>(current->word.substr(i),
                                                   current->is_end);

        current->word = current->word.substr(0, i);
        current->is_end = (i == str.size()) ? true : false;
        current->children.swap(new_node->children);
        current->children.insert(new_node);

        if (i != str.size()) {
          auto new_node2 = make_shared<RadixTreeNode>(str.substr(i), true);
          current->children.insert(new_node2);
        }
      } else {
        // 如果当前节点已匹配完，则继续往子节点匹配
        insert_helper(str.substr(i), current);
      }
      if (is_match) {
        return;
      }
    }
  }
  // 如果没有找到，则直接插入
  auto new_node = make_shared<RadixTreeNode>(str, true);
  node->children.insert(new_node);
}

删除

  1. 如果删除的是空字符串，则直接将 root 标记为非完整字符串。
  2. 遍历当前节点的子节点：
    • 当前节点的内容与字符串完全匹配：
      • 当前节点有子节点：将当前节点标记为非完整字符串。
      • 当前节点没子节点：直接删除该节点。此时如果在删除了该节点后，当前节点的父节点仅剩下一个子节点，并且父节点中存储一个不完整字符串，此时可以将当前节点和父节点合并，用于压缩路径。
    • 当前节点的内容是字符串的前缀：将字符串拆分为公共前缀和剩余后缀，用后缀继续向下递归查找到合适的位置进行删除。
    • 字符串是当前节点内容的前缀：该字符串一定不在树中，删除结束。
void erase(const string &str) {
  if (str.empty()) {
    root->is_end = false;
  } else {
    erase_helper(str, root);
  }
}

shared_ptr<RadixTreeNode> erase_helper(const string &str,
                                       shared_ptr<RadixTreeNode> node) {
  bool is_match = false;
  for (auto current : node->children) {
    int i = 0;
    for (; i < str.size() && i < current->word.size(); i++) {
      if (str[i] != current->word[i]) {
        break;
      }
    }
    if (i != 0) {
      is_match = true;

      // 情况一：当前节点的内容与字符串完全匹配
      if (i == str.size() && i == current->word.size()) {
        // 如果该节点没有子节点，则将该节点删除。否则将is_end标记为false
        if (current->children.empty()) {
          node->children.erase(current);
        } else {
          current->is_end = false;
        }

        // 如果删除了该节点后，父节点仅剩下一个子节点，且父节点不完整，则将两个节点合并
        if (node->children.size() == 1 && !node->is_end && node != root) {
          auto sub_node = *node->children.begin();
          node->children.erase(sub_node);
          node->is_end = sub_node->is_end;
          node->word.append(sub_node->word);
          node->children = sub_node->children;
          return node;
        }
      }
      // 情况二：当前节点是字符串的前缀
      else if (i == current->word.size()) {
        // 继续向下搜索，如果返回值不为空则说明需要合并节点
        auto sub_node = erase_helper(str.substr(i), current);
        if (sub_node && node->children.size() == 1 && !node->is_end &&
            node != root) {
          auto sub_node = *node->children.begin();
          node->children.erase(sub_node);
          node->is_end = sub_node->is_end;
          node->word.append(sub_node->word);
          node->children = sub_node->children;
        }
      }
      // 情况三：字符串是当前节点的前缀，此时字符串必定不存在，删除结束
      else {
        break;
      }
    }
    if (is_match) {
      return nullptr;
    }
  }
  return nullptr;
}

查找

查找实现的逻辑如下：

  1. 从根节点出发，如果字符串为空，判断空字符有没有存储到根节点，没有往下执行。
  2. 遍历当前节点的所有子节点，查找是否存在公共前缀，此时存在以下四种情况：
    • 当前节点的内容与字符串完全匹配：此时根据当前路径是否为完整单词，判断查找是否成功。
    • 当前节点的内容是字符串的前缀：将字符串拆分为前缀和剩余后缀，将后缀继续递归到该节点的子节点处继续查询，重复流程 2
    • 字符串是当前节点内容的前缀：查找失败，这一部分前缀必定没有插入到树中。
    • 无公共前缀：继续遍历下一个子节点，如果已经遍历完，则认为查找失败，该字符串不存在。
bool search(const string &str) {
  if (str.empty()) {
    return root->is_end;
  }
  return search_helper(str, root);
}

bool search_helper(const string &str, shared_ptr<RadixTreeNode> node) {
  for (auto current : node->children) {
    int i = 0;
    for (; i < str.size() && i < current->word.size(); i++) {
      if (str[i] != current->word[i]) {
        break;
      }
    }
    if (i != 0) {
      // 情况一：当前节点的内容与字符串完全匹配，根据是否为完整单词判断结果
      if (i == str.size() && i == current->word.size()) {
        return current->is_end;
      }
      // 情况二：当前节点的内容是字符串的前缀
      else if (i == current->word.size()) {
        return search_helper(str.substr(i), current);
      }
      // 情况三：字符串的内容是当前节点的前缀，直接返回错误
      else {
        return false;
      }
    }
  }
  // 没有找到
  return false;
}

完整代码

//
// Created by orekilee on 2023/3/31.
//

#ifndef RADIX_RADIXTREE_CPP
#define RADIX_RADIXTREE_CPP

#include <iostream>
#include <memory>
#include <string>
#include <unordered_set>

using namespace std;

class RadixTreeNode {
public:
  explicit RadixTreeNode(const string &word = "", bool is_end = false)
      : word(word), is_end(is_end) {}

  unordered_set<shared_ptr<RadixTreeNode>> children;
  string word;
  bool is_end;
};

class RadixTree {
public:
  RadixTree() : root(make_shared<RadixTreeNode>()){};

  virtual ~RadixTree() = default;

  RadixTree(const RadixTree &) = delete;
  RadixTree &operator=(const RadixTree &) = delete;

  void insert(const string &str) {
    if (str.empty()) {
      root->is_end = true;
    } else {
      insert_helper(str, root);
    }
  }

  void erase(const string &str) {
    if (str.empty()) {
      root->is_end = false;
    } else {
      erase_helper(str, root);
    }
  }

  bool search(const string &str) {
    if (str.empty()) {
      return root->is_end;
    }
    return search_helper(str, root);
  }

private:
  shared_ptr<RadixTreeNode> root;

  void insert_helper(const string &str, shared_ptr<RadixTreeNode> node) {
    // 如果当前没有子节点，则直接作为新的子节点
    if (node->children.empty()) {
      auto new_node = make_shared<RadixTreeNode>(str, true);
      node->children.insert(new_node);
      return;
    }

    bool is_match = false;
    for (auto current : node->children) {
      int i = 0;
      for (; i < str.size() && i < current->word.size(); i++) {
        if (str[i] != current->word[i]) {
          break;
        }
      }
      if (i != 0) {
        is_match = true;
        // 情况一：当前节点的内容与字符串完全匹配，则直接将该前缀标记为完整
        if (i == str.size() && i == current->word.size()) {
          current->is_end = true;
        } else if (i != current->word.size()) {
          // 如果当前节点的内容是字符串的部分前缀，则进行分裂
          auto new_node = make_shared<RadixTreeNode>(current->word.substr(i),
                                                     current->is_end);

          current->word = current->word.substr(0, i);
          current->is_end = (i == str.size()) ? true : false;
          current->children.swap(new_node->children);
          current->children.insert(new_node);

          if (i != str.size()) {
            auto new_node2 = make_shared<RadixTreeNode>(str.substr(i), true);
            current->children.insert(new_node2);
          }
        } else {
          // 如果当前节点已匹配完，则继续往子节点匹配
          insert_helper(str.substr(i), current);
        }
        if (is_match) {
          return;
        }
      }
    }
    // 如果没有找到，则直接插入
    auto new_node = make_shared<RadixTreeNode>(str, true);
    node->children.insert(new_node);
  }

  shared_ptr<RadixTreeNode> erase_helper(const string &str,
                                         shared_ptr<RadixTreeNode> node) {
    bool is_match = false;
    for (auto current : node->children) {
      int i = 0;
      for (; i < str.size() && i < current->word.size(); i++) {
        if (str[i] != current->word[i]) {
          break;
        }
      }
      if (i != 0) {
        is_match = true;

        // 情况一：当前节点的内容与字符串完全匹配
        if (i == str.size() && i == current->word.size()) {
          // 如果该节点没有子节点，则将该节点删除。否则将is_end标记为false
          if (current->children.empty()) {
            node->children.erase(current);
          } else {
            current->is_end = false;
          }

          // 如果删除了该节点后，父节点仅剩下一个子节点，且父节点不完整，则将两个节点合并
          if (node->children.size() == 1 && !node->is_end && node != root) {
            auto sub_node = *node->children.begin();
            node->children.erase(sub_node);
            node->is_end = sub_node->is_end;
            node->word.append(sub_node->word);
            node->children = sub_node->children;
            return node;
          }
        }
        // 情况二：当前节点是字符串的前缀
        else if (i == current->word.size()) {
          // 继续向下搜索，如果返回值不为空则说明需要合并节点
          auto sub_node = erase_helper(str.substr(i), current);
          if (sub_node && node->children.size() == 1 && !node->is_end &&
              node != root) {
            auto sub_node = *node->children.begin();
            node->children.erase(sub_node);
            node->is_end = sub_node->is_end;
            node->word.append(sub_node->word);
            node->children = sub_node->children;
          }
        }
        // 情况三：字符串是当前节点的前缀，此时必定查询失败
        else {
          break;
        }
      }
      if (is_match) {
        return nullptr;
      }
    }
    return nullptr;
  }

  bool search_helper(const string &str, shared_ptr<RadixTreeNode> node) {
    for (auto current : node->children) {
      int i = 0;
      for (; i < str.size() && i < current->word.size(); i++) {
        if (str[i] != current->word[i]) {
          break;
        }
      }
      if (i != 0) {
        // 情况一：当前节点的内容与字符串完全匹配，根据是否为完整单词判断结果
        if (i == str.size() && i == current->word.size()) {
          return current->is_end;
        }
        // 情况二：当前节点的内容是字符串的前缀
        else if (i == current->word.size()) {
          return search_helper(str.substr(i), current);
        }
        // 情况三：字符串的内容是当前节点的前缀，直接返回错误
        else {
          return false;
        }
      }
    }
    // 没有找到
    return false;
  }
};


#endif // RADIX_RADIXTREE_CPP

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/425879.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

[HNCTF 2022 Week1]Challenge__rce

[HNCTF 2022 Week1]Challenge__rce

1.打开环境。 查看源码传入hint获得源码。 <?php error_reporting(0); if (isset($_GET[hint])) {highlight_file(__FILE__); } if (isset($_POST[rce])) {$rce $_POST[rce];if (strlen($rce) < 120) {if (is_string($rce)) {if (!preg_match("/[!#%^&*:\-&…
阅读更多...
采集工具如何帮助SEO优化关键词

采集工具如何帮助SEO优化关键词

随着互联网的发展&#xff0c;越来越多的企业开始意识到SEO优化对于企业的重要性。SEO优化可以帮助企业提高网站在搜索引擎中的排名&#xff0c;进而吸引更多的潜在客户。而关键词则是SEO优化的核心&#xff0c;如何找到合适的关键词&#xff0c;成为了企业优化的关键。在这里&…
阅读更多...
ActiveMQ使用(三):在JavaScript中使用mqttws31.js

ActiveMQ使用(三):在JavaScript中使用mqttws31.js

ActiveMQ使用(三):在JavaScript中使用mqttws31.js 1. 环境准备 jQuery-1.10 下载地址:https://www.jsdelivr.com/package/npm/jquery-1.10.2?tabfilesmqttws31.js: 下载地址:https://www.jsdelivr.com/package/npm/ng2-mqtt 2. 相关代码 <!DOCTYPE html> <html …
阅读更多...
【GPT4】微软 GPT-4 测试报告（3）GPT4 的编程能力

【GPT4】微软 GPT-4 测试报告（3）GPT4 的编程能力

欢迎关注【youcans的GPT学习笔记】原创作品&#xff0c;火热更新中 微软 GPT-4 测试报告&#xff08;1&#xff09;总体介绍 微软 GPT-4 测试报告&#xff08;2&#xff09;多模态与跨学科能力 微软 GPT-4 测试报告&#xff08;3&#xff09;GPT4 的编程能力 【GPT4】微软 GPT-…
阅读更多...
在线绘制思维导图

在线绘制思维导图

思维导图是一种可视化的思维工具&#xff0c;它可以将放射性思考具体化为可视的图像和图表。 思维导图利用图文并重的技巧&#xff0c;把各级主题的关系用相互隶属与相关的层级图表现出来&#xff0c;把主题关键词与图像、颜色等建立记忆链接。 它运用图像和颜色等多种元素&…
阅读更多...
ctf做题记录本

ctf做题记录本

2023年3月16日 1.XXE漏洞 没做出来&#xff0c;bp上怎么不显示结果 https://blog.csdn.net/weixin_43553654/article/details/107760067?spm1001.2101.3001.6650.5&utm_mediumdistribute.pc_relevant.none-task-blog-2%7Edefault%7EESLANDING%7Edefault-5-107760067-blo…
阅读更多...
Java线上监控诊断产品Arthas

Java线上监控诊断产品Arthas

最近一直在研究Java的动态追踪技术&#xff0c;碰到了Arthas&#xff0c;正好以前也想学&#xff0c;趁此机会就了解了一下。 什么是Arthas&#xff1f;首先我们看看Arthas官方文档是怎么描述的&#xff1a; 什么是Arthas Arthas 是一款线上监控诊断产品&#xff0c;通过全局…
阅读更多...
欧拉函数及其线性筛

欧拉函数及其线性筛

一&#xff0c;定义 欧拉函数是对于n小于或者等于他的数中与n互质的数的个数。一般用φ(x)表示。 二&#xff0c;欧拉函数公式 其中pi为n的所有质因数。 公式的理解方法可以是pi是与n互质的数&#xff0c;那么它&#xff08;包括它的倍数&#xff09;在1~n里面是均匀出现的&…
阅读更多...
分布式场景下，Apache YARN、Google Kubernetes 如何解决资源管理问题？

分布式场景下，Apache YARN、Google Kubernetes 如何解决资源管理问题？

所有的资源管理系统都需要解决资源的有效利用、任务的有效响应、调度策略的灵活配置这三个最基本问题。那么在分布式的场景下&#xff0c;YARN和Kubernetes是怎么解决的呢&#xff1f;本篇进行介绍。 — Apache YARN — YARN全称为&#xff08;Yet Another Resource Negotiato…
阅读更多...
OSPF开放式最短路径优先协议

OSPF开放式最短路径优先协议

目录标题OSPF协议OSPF的数据包---5种OSPF的状态机OSPF的工作过程OSPF的基本配置关于ospf协议从邻居建立成为邻接的条件ospf的接口网络类型OSPF协议 是是无类别链路状态型IGP协议&#xff1b;由于其基于拓扑进行更新收敛&#xff0c;故更新量会随着拓扑的变大而呈指数上升&…
阅读更多...
处理CSV（python）

处理CSV（python）

处理CSV&#xff08;python&#xff09;简介1. CSV和Python简介2. 文章内容简介一、用csv模块读取和写入CSV文件1. CSV模块2. 示例二、用pandas库读取和写入CSV文件1. pandas2. 示例三、处理CSV文件中的特殊情况1. 特殊情况及处理方法2. 示例简介 1. CSV和Python简介 CSV是一…
阅读更多...
动态内存管理--从动态内存分配函数开始和你一起了解

动态内存管理--从动态内存分配函数开始和你一起了解

目录前言1.为什么存在动态内存分配2.动态内存函数的介绍2.1malloc函数和free函数2.2calloc函数2.3realloc函数3.常见的动态内存错误3.1对NULL指针的解引用操作3.2对动态开辟空间的越界访问3.3对非动态内存开辟的内存使用free释放3.4使用free释放一块动态内存的一部分3.5对同一块…
阅读更多...
【致敬未来的攻城狮计划】— 连续打卡第三天：欲速则不达，今天是对RA2E1 基础知识的补充学习。

【致敬未来的攻城狮计划】— 连续打卡第三天：欲速则不达，今天是对RA2E1 基础知识的补充学习。

系列文章目录 1.连续打卡第一天&#xff1a;提前对CPK_RA2E1是瑞萨RA系列开发板的初体验&#xff0c;了解一下 2.开发环境的选择和调试&#xff08;从零开始&#xff0c;加油&#xff09; 文章目录 目录 系列文章目录 文章目录 前言 一、RA是什么&#xff1f; 二、RA特点…
阅读更多...
RHCE——shell脚本练习

RHCE——shell脚本练习

一.实验要求 1、判断web服务是否运行&#xff08;1、查看进程的方式判断该程序是否运行&#xff0c;2、通过查看端口的方式判断该程序是否运行&#xff09;&#xff0c;如果没有运行&#xff0c;则启动该服务并配置防火墙规则。 ​2、使用curl命令访问第二题的web服务&#xff…
阅读更多...
Kafka的历史版本对应SpringBoot版本

Kafka的历史版本对应SpringBoot版本

截至目前&#xff08;2023年&#xff09;&#xff0c;Kafka的最新版本是2.9.0&#xff0c;发布于2022年11月30日。Kafka的历史版本可以在Kafka官方网站的下载页面中找到。Kafka从0.8版本开始发布&#xff0c;经历了多个版本的迭代和升级。以下是一些比较重要的Kafka版本及其发布…
阅读更多...
Python实现哈里斯鹰优化算法(HHO)优化Catboost回归模型(CatBoostRegressor算法)项目实战

Python实现哈里斯鹰优化算法(HHO)优化Catboost回归模型(CatBoostRegressor算法)项目实战

说明&#xff1a;这是一个机器学习实战项目&#xff08;附带数据代码文档视频讲解&#xff09;&#xff0c;如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 2019年Heidari等人提出哈里斯鹰优化算法(Harris Hawk Optimization, HHO)&#xff0c;该算法有较强的全…
阅读更多...
【LeetCode】剑指 Offer 52. 两个链表的第一个公共节点 p253 -- Java Version

【LeetCode】剑指 Offer 52. 两个链表的第一个公共节点 p253 -- Java Version

题目链接&#xff1a;https://leetcode.cn/problems/liang-ge-lian-biao-de-di-yi-ge-gong-gong-jie-dian-lcof/ 1. 题目介绍&#xff08;52. 两个链表的第一个公共节点&#xff09; 输入两个链表&#xff0c;找出它们的第一个公共节点。 如下面的两个链表&#xff1a; 在节点…
阅读更多...
基于微信小程序开发的“校园帮”系统

基于微信小程序开发的“校园帮”系统

基于微信小程序开发的“校园帮”系统【毕业论文&#xff0c;源码】 本系统使用了java和mysql结合的结构开发了微信小程序应用&#xff0c;系统中所有和数据库有关系的操作都通过一个通用类来实现&#xff0c;大大提高了代码的耦合性&#xff0c;当数据库类型等信息变化后直接修…
阅读更多...
【剑指offer|6.寻找峰值】

【剑指offer|6.寻找峰值】

0.寻找峰值 关键点: 返回任意一个峰值的下标即可nums[-1]nums[n]负无穷 输入&#xff1a;nums [1,2,3,1] 输出&#xff1a;2 解释&#xff1a;3 是峰值元素&#xff0c;你的函数应该返回其索引 2 1.傻瓜编程(纯属玩乐) class Solution { public:int findPeakElement(vector&l…
阅读更多...
普通人在家就能用ChatGPT轻松月赚$5000美金的方法

普通人在家就能用ChatGPT轻松月赚$5000美金的方法

太震撼了&#xff0c;这简直就是下个世纪才应该出现的产品&#xff0c;突然之间我感觉就像人类&#xff0c;刚刚发明了电灯一样&#xff0c;一切都要变了&#xff0c;而且变的速度太快&#xff0c;让我都觉得有点茫然了&#xff0c;绝对就是技术大爆炸。今天这篇文章我想通过ch…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023