1、题目如下：

2、个人Python代码实现：

         以上代码主要是照抄题解，根据调试bug了解每一步的逻辑，然后注释利于读懂本题，写本篇文章的目的在于初步了解动态规划。

        本题的逻辑主要如下：

        a、列表中每个数字代表当前路径的步数，整个代码的逻辑是将每个元素当前路径的步数转换成到当前路径的最小总步数

        b、以grid[1][0]、grid[0][1]为例，grid[0][0]的起始步数为1，grid[0][1]的步数为3，所以到grid[1][0]的总步数=grid[0][0] + grid[1][0]=3+1=4；同理grid[1][0]的总步数=grid[0][0] + grid[1][0]=1+1=2

        c、以grid[1][1]为例，到grid[1][1]有两种路径，分别是grid[1][0] + grid[1][1]和grid[0][1] + grid[1][1]，注意这里的grid[1][0]和grid[0][1]是逻辑b中计算的总步数（已标红），所以计算grid[1][1]的最小步数就是grid[1][0]和grid[0][1]的最小值再加上grid[1][1]的当前步数

        d、汇总逻辑b、c则如下：当当前元素在第一行时，元素的总步数一定是当前元素的步数加上左方元素的总步数；当当前元素在第一列时，元素的总步数一定是当前元素的步数加上上方元素的总步数；当当前元素既不在第一行、又不在第一列时，取上方、左方步数的较小值，再加上元素本身的步数，即为最小总步数。

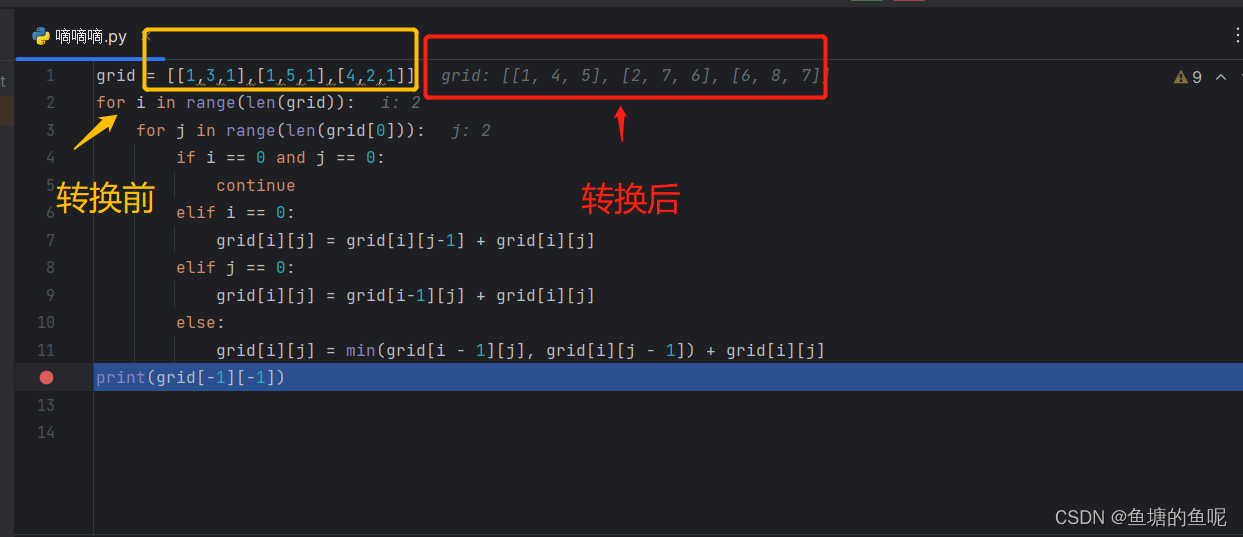
        通过以上逻辑，将路径上的数字，转换成到该路径的最小数字和，返回最后一个值即可，下图，即为示例转换后的列表：

3、Java代码实现： 

        这里注意三点（个人犯的错，记录）：

        a、Java语法是else if 而不是elif

        b、Java可以通过Math.min取最小值

        c、Java不能写成grid[-1][-1]