目录

1. 概述

2. 连续信号分析

2.1 等变网络层

3. 具体实现

3.1 傅里叶特征和基础简化

3.2 根据连续插值进行的步骤重建

4.实验

总结

Reference

关于StyleGAN系列博客的收尾之作，StyleGAN3已经鸽了太久了。说实话，前两篇StyleGAN说的什么内容，我自己都快忘记了。这里把链接放出来，方便大家复习：

StyleGAN1：用于人脸生成的StyleGAN结构

StyleGAN2：改善StyleGAN的图像质量

关于StyleGAN3[1]，其贡献已经在题目中说的非常清楚了，不受坐标限制（Alias-Free）。在没有认真看正文文字内容的前提下，仅通过上面的图片，我对StyleGAN3实现的猜测是，首先找到对应的语义区域，之后建立非刚性的对应关系，在此基础上指导生成模型，并控制生成对象不超过语义限定区域，使得整个变换过程类似于非刚性形变过程。带着这样一种猜测，我们来看一下StyleGAN3的具体实现。

1. 概述

首先让我们回顾一下，在StyleGAN2中，其主要的贡献是重新设置了style block的结构，移除了artifacts，并且结合了图像质量评价，使得生成的图片更加自然，更符合人类的主观认知。但是，在StyleGAN2从噪声恢复出结果图片的过程，每个像素是受到坐标系的控制，而不是对应的实际语义对象。这个缺陷使得图片在变化过程中，会造成局部区域的变换结果存在模糊，甚至破坏了语义对象对应区域的图像细节，如下图所示。

该缺点是显而易见的，因为在StyleGAN2的生成模型没有考虑严格的语义约束，使得和语义对象相邻的外部像素也被混合进生成模型中，这个缺陷产生的像素异常（颜色的堆叠），在连续变换中尤其明显。作者给出了更直观的解释：当一个人扭头时，那么他的鼻子，相关的纹理也会按照扭头的旋转来产生位移。但是目前的GAN不考虑这种位移，而是将低分辨率特征按照层级结构进行上采样，再通过卷积混合。试想，如果我们希望用GAN来合成一个人扭头的视频，那么传统的方法一定会产生一个非常不自然的画面：一个人的脸一会变成背景，一会又变成脸了。为了解决该问题，Alias-Free的StyleGAN3被提出。

StyleGAN3的目标是揭示一个更加自然的层级变换，每个特征的精确像素位置从底层特征继承。作者认真的调研了StyleGAN2结构中产生混叠的原因，发现当前的上采样滤波器在抑制混叠方面根本不够积极，这里需要衰减超过100dB的高质量滤波器（不懂啥意思）。进一步地，作者提出了一个原则性的解决方案，由pointwise的非线性[2]引起的混叠，通过考虑它们在连续域的影响和适当的低通滤波产生结果。经过调整后，作者发现一个基于1*1卷积的模型实现了一个强大的，等同于旋转变换的生成器。自然的，新的GAN结果对于视频与动画生成任务带来显著的性能提升。

注：这篇文章反复提到一个词：equivariance，确实不知道准确翻译。大概意思就是不受某种变换影响的意思，但是为什么不用invariant呢？

2. 连续信号分析

作者在这里首先分析了信号在网络的流动。虽然数据是在像素网格中存储，但我们不能直接使用这些数据来表示信号。这样使得我们可以进行更加精确的连续信号分析。根据奈奎斯特-香农抽样定理，一个有规律采样的信号，可以表示任何频率在零到采样率的一半之间的连续信号。让我们考虑一个二维的，离散的采样特征图Z[x], 它由一个定期分布在1/s单位间隔内，大小不同的Dirac冲击序列组成，其中s是采样率。这类似于无限的二维值网格。

给定Z[x]和s，惠特克-香农插值公式说明对应连续的表示z(x)获取自卷积离散采样Dirac网格Z[x], 伴随一个理想的插值滤波，，其中*表示连续的卷积，采用信号处理公约：，其中

采用了带宽限制s/2沿着水平和垂直两个维度。保证了在所有可被s表示的频率产生连续的信号捕获。（注：完全不懂说的什么东西，基本都是信号处理领域的内容）

从连续域到离散域的转换对应于对连续信号z(x)进行采样，采样点为Z[x]的采样点，我们定义采样点的偏移量为半个采样间隔，以便位于“像素中心”，如下图：

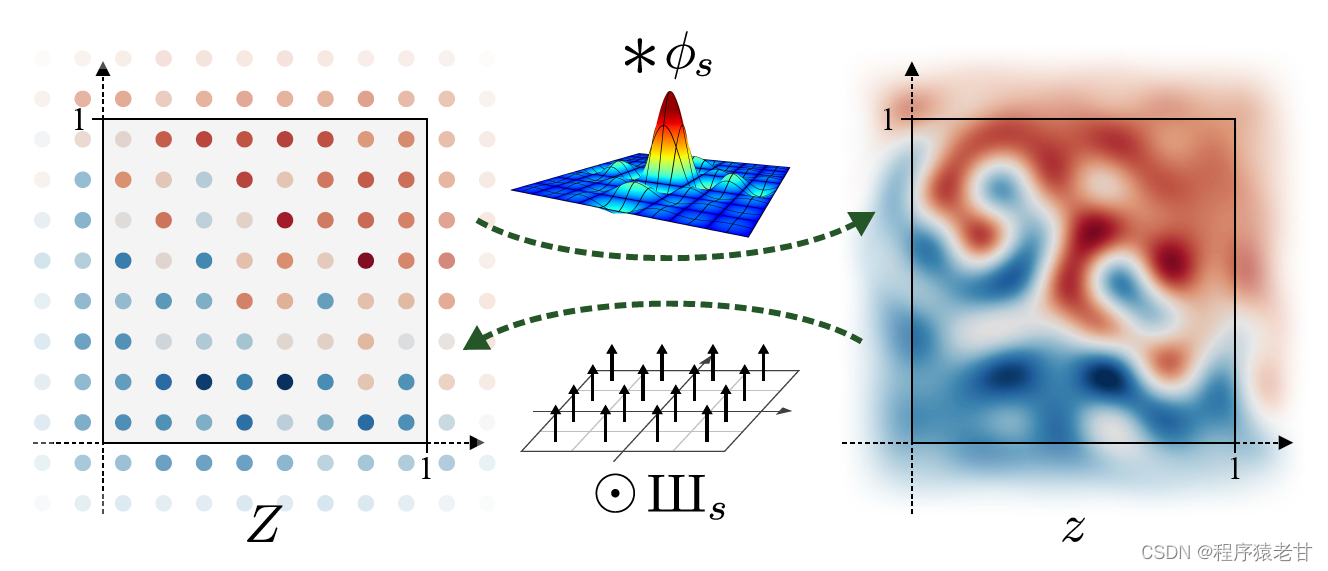
作者在z(x)中指定了单位方格，作为感兴趣信号区域，对应Z[x]的尺度为s*s。但是，这里从连续的角度看，不应该只是s*s，因为外部的一些信息也会影响s*s内部。因此，我们要存比s*s稍大一点的区域作为分析区域。通过建立起有限带宽、连续特征映射z(x)和离散采样特征映射Z[x]之间的对应关系，我们可以将注意力从信号的像素中心视角中移开。在本文的剩余部分，我们将把z(x)解释为实际被操作的信号，而离散采样特征映射Z[x]仅仅是它的一个方便的编码形式。

网络层中离散和连续的表示。实用的神经网络执行在离散采样的特征图上。考虑到操作符F执行一个离散的特征图：。该特征图有一个对应的连续形式。因此，我们在连续域中也获得了一个映射。现在，可以看到在一个域中指定的操作，在另一个域中也可执行相应的操作：

表示逐点乘法，s和s0是输入和输出采样率，注意，后一种情况f不能引入超过输出带宽

的频率内容。

2.1 等变网络层

如果关于2D平面的空间变换t与操作f在连续域中可交换，则操作f对于空间变换t是等变的：

作者关注于两种满足同变性的变换：平移和旋转。对于旋转来说，谱约束会更强：旋转一幅图像相当于旋转光谱。为了保证水平方向和垂直方向的带宽限制，必须将频谱限制在半径为s=2的圆盘上，这既适用于初始网络输入，也适用于用于下采样的带宽限制滤波器。

接下来需要考虑生成中的四个基本步骤：convolution, upsampling,downsampling, and nonlinearity。在不丧失一般性的情况下，我们讨论作用于单个特征图的操作：对分析没有影响的特征逐点线性组合。

Convolution：考虑一个标准卷积，kernal K，我们可以将K解释为与输入特征映射相同的对应网格，采样率为s。离散域的操作是简单的：

我们获得对应的连续操作符：

由于卷积的可交换性，以及理想低通滤波卷积的离散化，伴随相同的采样率，是一个恒等运算（identity operation）。

换句话说，卷积是通过在特征映射的连续表示上连续滑动离散化核来操作的。这个卷积没有引入新的频率。因此，平移和旋转对带宽限制要求得到了很好的满足。卷积在连续域中也满足平移交换律，因此该操作对平移是等变的。对于旋转等变性，离散核K需要是径向对称的。

上采样和下采样：理想的上采样不会改变连续表示，仅是提高输出的采样率s‘>s，来增加频域中的余量，为后续层可能引入的额外内容提供空间。这里用两段内容介绍了关于在离散域上采样以及使用低通滤波z移除超过带宽的频率，并实现下采样。

非线性特征：在离散域中应用一个pointwise的非线性特征σ不能满足部分平移或旋转运算。但是在连续域，任何pointwise的函数都与几何变换可交换，因此对于平移和旋转是等变的。实现带宽限制约束是另一个应用问题，例如，连续域中的ReLU可能会引入无法在输出中表示的任意高频率。

一种自然的解决方案是用理想的低通滤波器对连续结果进行卷积来消除高频内容。于是，非线性特征的连续表示变成了：

其离散对应为：

如图所示：

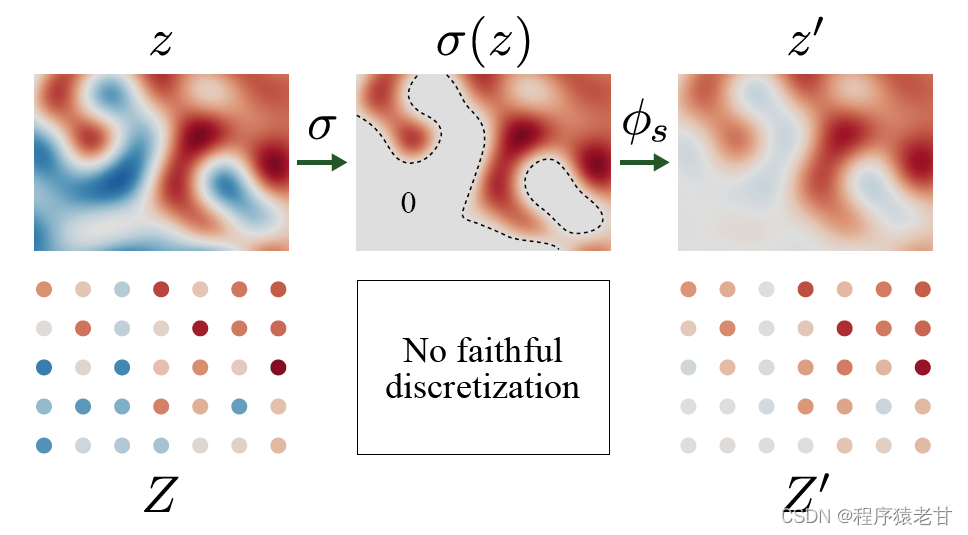
这个离散计算需要进入连续表示才能实现。我们使用上采样信号来近似连续表示，在更高的分辨率中应用非线性特征，随后进行下采样。虽然非线性特征仍然是在离散域被分析，作者发现只要进行2倍的分辨率提升，就足够支持高质量的同变性。对于旋转同变性，我们必须在下采样阶段使用径向对称插值滤波器。注意，非线性特征计算是唯一产生新频率的操作，作者提出可以在最后的离散化操作前，应用一个重建的，具有低截止点的（<s/2）滤波器来限制这些新产生的频率。这能让我们精确的控制在生成器中，各层引入的新信息。由于我不太了解信号处理的基础知识，所以这部分内容很多知识点不太理解，部分内容是猜着翻译的，有兴趣的同学可以看下原文。

3. 具体实现

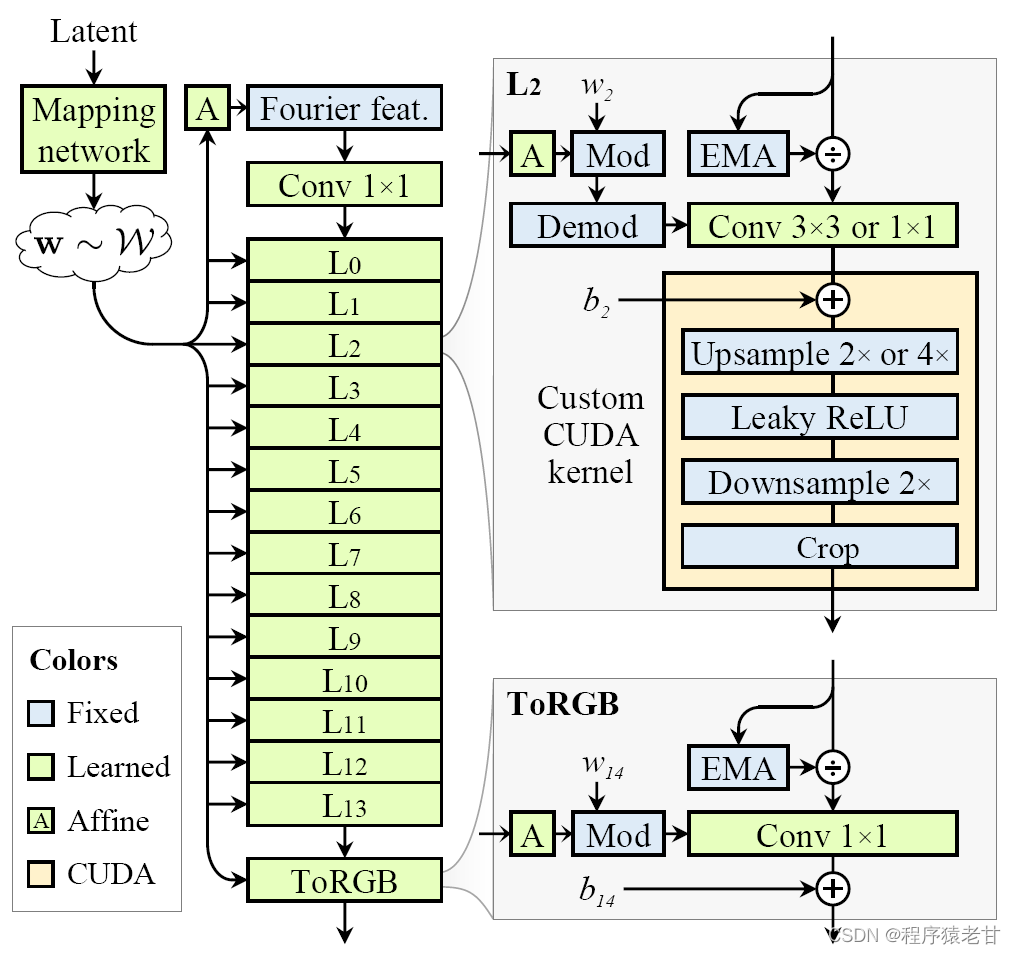
作者根据之前信号分析的基本理论构想，提供了具体的生成器改进方法，以解决平移旋转的问题。整个结构均是基于StyleGAN2进行的改进。StyleGAN2包含两个部分，一个mapping网络（变换一个初始的，正态分布latent到一个中间的latent编码，），一个合成网络（从一个4*4*512的常矢量Z0开始到应用一个N层的序列，由间距，非线性计算，上采样，逐像素噪声，以产生一个输出图像，）。中间隐层编码w控制G内部卷积核的调制。

StyleGAN3的目标是使G中的每一层相对于连续信号都是等变的，这使得所有细节变换全部对应在一个局部邻域的粗略特征。换句话说，作者希望在合成网络中创造等边的连续操作g以适配变换t（包含平移与旋转），以应用于连续的输入：。评估各种架构变化和实际近似的影响，需要一个方式去度量网络等变性的执行质量。对于平移等变，作者在两组图像之间报告了基于分贝的指标：peak signal-to-noise ratio (PSNR)，类似于[3]:

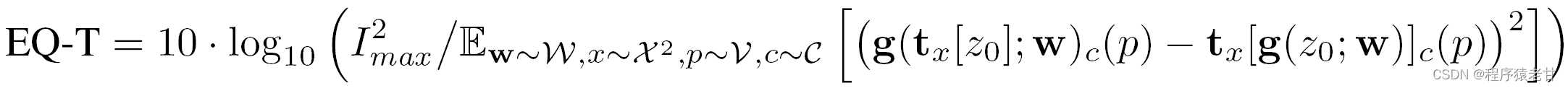
每一对图像，对应一个不同的w随机选择，并被采样为整数的像素位置p伴随其交叉有效区域V。颜色通道c被独立处理，所生成图像的预期动态范围-1~+1，Imax=2。操作符tx执行对二维偏移量x的频域变换，这里来自整数抵消的分布。这里定义一个用于旋转，角度取

3.1 傅里叶特征和基础简化

为了对输入进行连续精确的连续变化，作者替换了StyleGAN2使用的常矢量输入，使用傅里叶特征作为新的输入。这有助于顶一个在空间的无限映射。作者按照周期性频段fc=2来均匀的采样频率，匹配原始的4*4输入分辨率，并且使他们在训练过程中保持固定。这个变化平滑的提升FID，更关键的是允许我们在不知道t变换近似的前提下，来计算等变度量。这个基准结构还不是等变的。

之后，作者移除了像素级噪声输入，原因是这些输入与建立实现自然转换的层次结构的目标非常不一致。也就是，每一个精确的像素位置是完全继承自底层的粗糙特征。这个过程类似于FID-neutral，但是FID-neutral不能改善等变性度量。

为了进一步简化设置，作者降低了映射网络的深度，关闭了混合与路径正则化。最后，作者去掉了输出的skip connections。作者假设了这些功能块的贡献在于训练过程的动态梯度优化，在每次卷积之前使用简单的归一化更直接地解决潜在问题。作者追踪指数移动平均线，追踪执行在所有像素和特征图上，按照分割特征图。实际上，作者将除法嵌入卷积权重中以提高效率。这些更改(配置D：Simplified generator)将FID带回原始StyleGAN2的级别，同时对平移等变性产生一定程度的提升。

3.2 根据连续插值进行的步骤重建

边界和上采样。我们的理论为特征空间假设了一个无限的空间扩展，我通过在目标画布周围保留一个固定尺度的差额来实现逼近，在每一层将其修正到扩展画布。这个显示扩展是必要的，因为已知的边界填充泄漏了绝对图像坐标到内部表示。实践中，我们发现一个10个像素的差额就足够了，再扩展没啥意义。

基于我们的理论模型，我们将双线性两倍上采样滤波器替换为理想的近似低通滤波器。我们使用一个带窗口的sinc滤波器，其大小为n = 6的相对较大的Kaiser窗口，这意味着每个输出像素在上采样时受到6个输入像素的影响，在下采样时每个输入像素影响6个输出像素。Kaiser窗口很好用，因为它可以对过渡带和衰减程度进行明确的显性控制。提醒一下，我们明确地指定了过渡带，并使用Kaiser的原始公式计算其余参数。这里，我们选择使用临界抽样和设置滤波器截止频率fc=s/2。正好在带宽限制，过渡带半宽处fh=(根号2-1)(s/2)。回想一下，根据我们在第2节中的定义，采样率s等于画布的宽度(以像素为单位)。

改进的边界处理和上采样提供了更好的等值变换。但是，FID降低了16%，可能是因为我们开始限制特征映射可以包含的内容。在进一步的消融实验中，更小的采样滤波器波坏了等值变换，同时更大的滤波器又增加了训练时间。滤波后的非线性，我们非线性的理论处理方式要求为某些放大系数m，在m倍上采样和m倍下采样之间，将每个漏性ReLU(或者其他的通用非线性)进行包裹。我们发现，由于信号带宽被限制，使得上采样和卷积的顺序可互换。这让我们可以融合常规的两倍上采样和一个m被的上采样，关联到非线性的一个独立的2m倍的上采样。实际上，我们发现m=2是足够的，进一步提升了EQ-T。使用当前的深度学习单元来执行上采样-LReLu-下采样序列不可行。因此我们执行一个自定义的CUDA核结合那些操作符，获得10倍的速度提升，并节省存储需求。

非关键采样。关键采样策略，即滤波器截止点被精确地设置在带宽限制上，是一个理想的情况，对于众多图像处理应用来说，因为它在抗锯齿和保留高频细节之间取得了很好的平衡。然而，我们的目标明显不同，因为混叠对生成器的等值方差是非常不利的。同时，高频信息对于输出图像来说是非常重要的，因为是在高分辨层，在更早期的层并不重要，因为它们的分辨率从开始看有些随机。

为了抑制混叠，我们可以简单地降低截止频率到fc=s/2-fh,这保证了所有的大于s/2的人造频率在抑制频带上。实践中，除去最高分辨率的那些层，我们选择降低每层的fc。因为最后生成器必须能够生成清晰的图像来匹配训练数据。由于信号包含较少的空间信息，我们修改了用于确定特征映射数量的启发式，使其与fc而不是采样率s成反比。这些变化(配置G)进一步改善了等值变换，并将FID推到原来的StyleGAN2以下。

变换后的傅里叶特征。等值生成器层很好的适配建模未对齐的和任意定向的数据集，因为对中间特征zi引入的任何几何变换，都将直接携带到最终的图像zN。然而，由于层本身引入全局转换的能力有限，输入特征z0扮演一个关键的角色在定义的全局定位zN。为了让每个图像的方向不同，生成器应该具备能力来基于w来变换z0。这促使我们引入一个学习仿射层，以傅里叶特征为输入，并输出全局变换和旋转参数。层被初始化来执行一个恒等交换，但是学习使用机制也会带来较大的时间开销。

灵活的层规格。我们的改变已经有效的提升了等值质量，但是一些可以看到的加工痕迹依然存在。仔细观察，对于最低分辨率的层，我们的滤波器(配置G中定义的)的衰减仍然不够。这些层趋向于拥有接近于他们带宽的更丰富的频率信息，这需要非常强的衰减来完全消除混叠。到目前为止，我们已经使用了StyleGAN2的刚性采样率级数，再加上滤波器截止fc和半宽fh的简单选择，但这并不一定是这样；我们能够在每层自由的指定参数。尤其是，我们更喜欢fh在低分辨率层中尽可能高，但是在高分辨层中尽可能低，以允许在训练数据中匹配高频细节。

新层的指定又一次提升了等值变换质量，消除了残留的人工痕迹。一个进一步的消融实验展示出ft0提供了一个有效的方式来以训练速度换取等值质量。注意层的数量现在一个自由的参数，这不依赖于输出的分辨率。其实我们已经发现了固定的选择N在多个输出分辨率上始终如一地工作，并使其他超参数(如学习率)的行为更可预测。这里的N选为14.

旋转等值。我们使用两个变换来获得了网络的一个旋转等值版本，首先，我们在所有的层使用1*1卷积替换3*3卷积，并且通过将特征映射的数量增加一倍来弥补容量的减少。在这个配置中，只有上采样和下采样操作在像素之间传播信息。其次，我们用一个使用相同的Kaiser方案构造的基于径向对称的jinc的下采样滤波器替换基于sinc的下采样滤波器。我们将该操作应用于所有层，除去两个关键的采样版本，匹配训练数据潜在的放射光谱非是非常重要的。这些变化改善了EQ-R同时不会伤害FID，甚至每一层减少了56%的训练参数。在这个配置中，我们还使用了一个额外的稳定技巧。在训练的早期，我们使用高斯滤波器模糊鉴别器看到的所有图像。我们开始设置σ=10个像素，在前20万张图像中，我们将其变成零。这防止了鉴别器在早期过于集中在高频信息。如果没有这个技巧，配置R很容易出现早期崩溃，因为生成器有时学习产生高频时会有较小的延迟，从而轻视了鉴别器的任务。

4.实验

总结

大篇幅的信号处理相关的内容，包括傅里叶特征，带宽，频率等等，对应GAN网络相关配置的描述，我确实没有理解。为了实现高效的等值变换，似乎要对每一层各频段信息做精确的控制。上下采样的配合，高频低频信息的组合也尤其重要。我认为如果想真正理解该篇论文的核心思想，恐怕还是要要补一补信号处理相关的知识。这篇论文的附录非常丰富，介绍了非常多的技术细节，童工了进一步的理论解释，有兴趣的小伙伴可以看看。

Reference

[1] T. Karras, M. Aittala, S. Laine, et al. Alias-free generative adversarial networks[J]. Advances in Neural Information Processing Systems, 2021, 34: 852-863.

[2] A. Azulay and Y. Weiss. Why do deep convolutional networks generalize so poorly to small image transformations? Journal of Machine Learning Research, 20(184):1–25, 2019.

[3] R. Zhang. Making convolutional networks shift-invariant again. In Proc. ICML, 2019