LeetCode算法小抄--二叉搜索树
- 二叉搜索树(BST)
- 寻找第 K 小的元素
- [230. 二叉搜索树中第K小的元素](https://leetcode.cn/problems/kth-smallest-element-in-a-bst/)
- 二叉搜索树的转化
- [538. 把二叉搜索树转换为累加树](https://leetcode.cn/problems/convert-bst-to-greater-tree/)
- [1038. 从二叉搜索树到更大和树](https://leetcode.cn/problems/binary-search-tree-to-greater-sum-tree/)
- 判断 BST 的合法性
- [98. 验证二叉搜索树](https://leetcode.cn/problems/validate-binary-search-tree/)
- 在 BST 中搜索元素
- [700. 二叉搜索树中的搜索](https://leetcode.cn/problems/search-in-a-binary-search-tree/)
- 在 BST 中插入一个数
- [701. 二叉搜索树中的插入操作](https://leetcode.cn/problems/insert-into-a-binary-search-tree/)
- 在 BST 中删除一个数
- 完整版
- [450. 删除二叉搜索树中的节点](https://leetcode.cn/problems/delete-node-in-a-bst/)
- 构造BST
- [96. 不同的二叉搜索树](https://leetcode.cn/problems/unique-binary-search-trees/)
- [95. 不同的二叉搜索树 II](https://leetcode.cn/problems/unique-binary-search-trees-ii/)
⚠申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计9437字,阅读大概需要10分钟
🌈更多学习内容, 欢迎👏关注👀【文末】我的个人微信公众号:不懂开发的程序猿
个人网站:https://jerry-jy.co/
二叉搜索树(BST)
二叉查找树:又被称为二叉搜索树(Binary Search Tree,简写 BST)其特点如下
1、对于 BST 的每一个节点 node,左子树节点的值都比 node 的值要小,右子树节点的值都比 node 的值大。
2、对于 BST 的每一个节点 node,它的左侧子树和右侧子树都是 BST。
3、”中序遍历“可以让结点有序(升序)。
直接基于 BST 的数据结构有 AVL 树,红黑树等等,拥有了自平衡性质,可以提供 logN 级别的增删查改效率;还有 B+ 树,线段树等结构都是基于 BST 的思想来设计的
寻找第 K 小的元素
230. 二叉搜索树中第K小的元素
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。
一个直接的思路就是升序排序,然后找第 k 个元素呗。BST 的中序遍历其实就是升序排序的结果,找第 k 个元素肯定不是什么难事。
class Solution {
public int kthSmallest(TreeNode root, int k) {
// 利用 BST 的中序遍历特性
traverse(root, k);
return res;
}
// 记录结果
int res = 0;
// 记录当前元素的排名
int rank = 0;
private void traverse(TreeNode root, int k){
if(root == null) return;
traverse(root.left, k);
/* 中序遍历代码位置 */
rank++;
if(k == rank){
// 找到第 k 小的元素
res = root.val;
return;
}
traverse(root.right, k);
}
}
二叉搜索树的转化
538. 把二叉搜索树转换为累加树
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
对于一个节点来说,确实右子树都是比它大的元素,但问题是它的父节点也可能是比它大的元素呀?这个没法确定的,我们又没有触达父节点的指针,所以二叉树的通用思路在这里用不了。
其实,正确的解法很简单,还是利用 BST 的中序遍历特性。
如果我想降序打印节点的值怎么办?
很简单,只要把递归顺序改一下就行了:
void traverse(TreeNode root) {
if (root == null) return;
// 先递归遍历右子树
traverse(root.right);
// 中序遍历代码位置
print(root.val);
// 后递归遍历左子树
traverse(root.left);
}
这段代码可以降序打印 BST 节点的值,如果维护一个外部累加变量 sum,然后把 sum 赋值给 BST 中的每一个节点,不就将 BST 转化成累加树了吗?
class Solution {
public TreeNode bstToGst(TreeNode root) {
traverse(root);
return root;
}
// 记录累加和
int sum = 0;
private void traverse(TreeNode root) {
if (root == null) {
return;
}
traverse(root.right);
// 维护累加和
sum += root.val;
// 将 BST 转化成累加树
root.val = sum;
traverse(root.left);
}
}
这道题就解决了,核心还是 BST 的中序遍历特性,只不过我们修改了递归顺序,降序遍历 BST 的元素值,从而契合题目累加树的要求。
1038. 从二叉搜索树到更大和树
给定一个二叉搜索树 root (BST),请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。
提醒一下, 二叉搜索树 满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
class Solution {
public TreeNode bstToGst(TreeNode root) {
traverse(root);
return root;
}
// 记录累加和
int sum = 0;
private void traverse(TreeNode root) {
if (root == null) {
return;
}
traverse(root.right);
// 维护累加和
sum += root.val;
// 将 BST 转化成累加树
root.val = sum;
traverse(root.left);
}
}
判断 BST 的合法性
98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
boolean isValidBST(TreeNode root) {
if (root == null) return true;
// root 的左边应该更小
if (root.left != null && root.left.val >= root.val)
return false;
// root 的右边应该更大
if (root.right != null && root.right.val <= root.val)
return false;
return isValidBST(root.left)
&& isValidBST(root.right);
}
坑:
这个算法出现了错误,BST 的每个节点应该要小于右边子树的所有节点,下面这个二叉树显然不是 BST,因为节点 10 的右子树中有一个节点 6,但是我们的算法会把它判定为合法 BST:

出现问题的原因在于,对于每一个节点 root,代码值检查了它的左右孩子节点是否符合左小右大的原则;但是根据 BST 的定义,root 的整个左子树都要小于 root.val,整个右子树都要大于 root.val。
问题是,对于某一个节点 root,他只能管得了自己的左右子节点,怎么把 root 的约束传递给左右子树呢?
class Solution {
public boolean isValidBST(TreeNode root) {
return isValidBST(root, null, null);
}
/* 限定以 root 为根的子树节点必须满足 max.val > root.val > min.val */
private boolean isValidBST(TreeNode root, TreeNode min, TreeNode max){
// base case
if(root == null) return true;
// 若 root.val 不符合 max 和 min 的限制,说明不是合法 BST
if(min != null && root.val < min.val) return false;
if(max != null && root.val > max.val) return false;
// 限定左子树的最大值是 root.val,右子树的最小值是 root.val
return isValidBST(root.left, min, root) && isValidBST(root.right, root, max);
}
}
通过使用辅助函数,增加函数参数列表,在参数中携带额外信息,将这种约束传递给子树的所有节点,这也是二叉树算法的一个小技巧吧。
在 BST 中搜索元素
700. 二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
class Solution {
//在一棵普通的二叉树中寻找,可以这样写
public TreeNode searchBST(TreeNode root, int val) {
if(root == null) return null;
if(root.val == val) return root;
// 当前节点没找到就递归地去左右子树寻找
TreeNode left = searchBST(root.left, val);
TreeNode right = searchBST(root.right, val);
return left != null? left : right;
}
}
这样写完全正确,但这段代码相当于穷举了所有节点,适用于所有二叉树。那么应该如何充分利用 BST 的特殊性,把「左小右大」的特性用上?
很简单,其实不需要递归地搜索两边,类似二分查找思想,根据 target 和 root.val 的大小比较,就能排除一边。我们把上面的思路稍稍改动
class Solution {
//在一棵普通的二叉树中寻找,可以这样写代码
public TreeNode searchBST(TreeNode root, int val) {
if(root == null) return null;
if(root.val == val) return root;
if(val < root.val){
return searchBST(root.left, val);
}
if(val > root.val){
return searchBST(root.right, val);
}
return root;
}
}
在 BST 中插入一个数
对数据结构的操作无非遍历 + 访问,遍历就是「找」,访问就是「改」一旦涉及「改」,就类似二叉树的构造问题,函数要返回 TreeNode 类型,并且要对递归调用的返回值进行接收。
TreeNode insertIntoBST(TreeNode root, int val) {
// 找到空位置插入新节点
if (root == null) return new TreeNode(val);
// if (root.val == val)
// BST 中一般不会插入已存在元素
if (root.val < val)
root.right = insertIntoBST(root.right, val);
if (root.val > val)
root.left = insertIntoBST(root.left, val);
return root;
}
701. 二叉搜索树中的插入操作
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
// 找到空位置插入新节点
if(root == null) return new TreeNode(val);
if(val > root.val) root.right = insertIntoBST(root.right, val);
if(val < root.val) root.left = insertIntoBST(root.left, val);
return root;
}
}
在 BST 中删除一个数
跟插入操作类似,先「找」再「改」
TreeNode deleteNode(TreeNode root, int key) {
if (root.val == key) {
// 找到啦,进行删除
} else if (root.val > key) {
// 去左子树找
root.left = deleteNode(root.left, key);
} else if (root.val < key) {
// 去右子树找
root.right = deleteNode(root.right, key);
}
return root;
}
找到目标节点了,比方说是节点 A,如何删除这个节点,这是难点。因为删除节点的同时不能破坏 BST 的性质。有三种情况
情况 1:A 恰好是末端节点,两个子节点都为空,就直接删除。
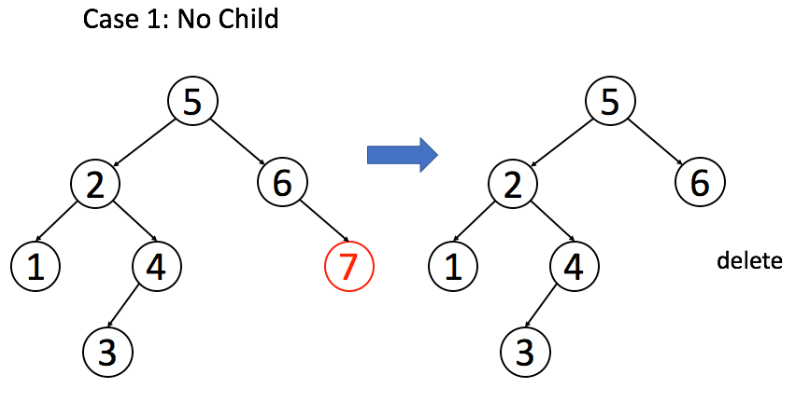
if (root.left == null && root.right == null)
return null;
情况 2:A 只有一个非空子节点,那么它要让这个孩子接替自己的位置。

// 排除了情况 1 之后
if (root.left == null) return root.right;
if (root.right == null) return root.left;
情况 3:A 有两个子节点,麻烦了,为了不破坏 BST 的性质,A 必须找到左子树中最大的那个节点,或者右子树中最小的那个节点来接替自己。我们以第二种方式讲解。
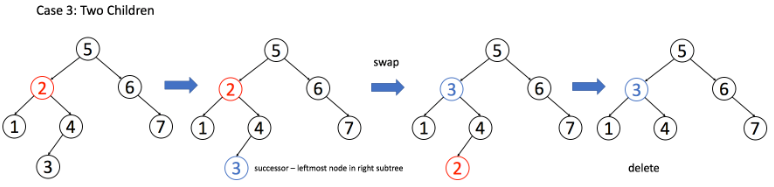
if (root.left != null && root.right != null) {
// 找到右子树的最小节点
TreeNode minNode = getMin(root.right);
// 把 root 改成 minNode
root.val = minNode.val;
// 转而去删除 minNode
root.right = deleteNode(root.right, minNode.val);
}
完整版
TreeNode deleteNode(TreeNode root, int key) {
if (root == null) return null;
if (root.val == key) {
// 这两个 if 把情况 1 和 2 都正确处理了
if (root.left == null) return root.right;
if (root.right == null) return root.left;
// 处理情况 3
// 获得右子树最小的节点
TreeNode minNode = getMin(root.right);
// 删除右子树最小的节点
root.right = deleteNode(root.right, minNode.val);
// 用右子树最小的节点替换 root 节点
minNode.left = root.left;
minNode.right = root.right;
root = minNode;
} else if (root.val > key) {
root.left = deleteNode(root.left, key);
} else if (root.val < key) {
root.right = deleteNode(root.right, key);
}
return root;
}
TreeNode getMin(TreeNode node) {
// BST 最左边的就是最小的
while (node.left != null) node = node.left;
return node;
}
注意一下,上述代码在处理情况 3 时通过一系列略微复杂的链表操作交换 root 和 minNode 两个节点:
// 处理情况 3
// 获得右子树最小的节点
TreeNode minNode = getMin(root.right);
// 删除右子树最小的节点
root.right = deleteNode(root.right, minNode.val);
// 用右子树最小的节点替换 root 节点
minNode.left = root.left;
minNode.right = root.right;
root = minNode;
替换 root 节点为什么这么麻烦,直接改 val 字段不就行了?看起来还更简洁易懂
// 处理情况 3
// 获得右子树最小的节点
TreeNode minNode = getMin(root.right);
// 删除右子树最小的节点
root.right = deleteNode(root.right, minNode.val);
// 用右子树最小的节点替换 root 节点
root.val = minNode.val;
仅对于这道算法题来说是可以的,但这样操作并不完美,我们一般不会通过修改节点内部的值来交换节点。因为在实际应用中,BST 节点内部的数据域是用户自定义的,可以非常复杂,而 BST 作为数据结构(一个工具人),其操作应该和内部存储的数据域解耦,所以我们更倾向于使用指针操作来交换节点,根本没必要关心内部数据
450. 删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if(root == null) return null;
if(root.val == key){
if(root.left == null) return root.right;
if(root.right == null) return root.left;
// 获得右子树最小的节点
TreeNode minNode = getMin(root.right);
// 删除右子树最小的节点
root.right = deleteNode(root.right, minNode.val);
// 用右子树最小的节点替换 root 节点
root.val = minNode.val;
} else if(key > root.val){
root.right = deleteNode(root.right, key);
}else if(key < root.val){
root.left = deleteNode(root.left, key);
}
return root;
}
private TreeNode getMin(TreeNode node){
// BST 最左边的就是最小的
while(node.left != null){
node = node.left;
}
return node;
}
}
构造BST
96. 不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
// 超出时间限制
class Solution {
public int numTrees(int n) {
return count(1, n);
}
/* 计算闭区间 [lo, hi] 组成的 BST 个数 */
private int count(int lo, int hi) {
// base case
if (lo > hi) return 1;
int res = 0;
for (int i = lo; i <= hi; i++) {
// i 的值作为根节点 root
int left = count(lo, i - 1);
int right = count(i + 1, hi);
// 左右子树的组合数乘积是 BST 的总数
res += left * right;
}
return res;
}
}
// 优化算法,备忘录模式
class Solution {
// 备忘录
int[][] memo;
public int numTrees(int n) {
memo = new int[n+1][n+1];
return count(1, n);
}
private int count(int lo, int hi) {
if(lo > hi) return 1;
// 查备忘录
if(memo[lo][hi] != 0){
return memo[lo][hi];
}
int res = 0;
for(int mid = lo; mid <= hi; mid++) {
int left = count(lo, mid-1);
int right = count(mid+1, hi);
res += left * right;
}
// 将结果存入备忘录
memo[lo][hi] = res;
return res;
}
}
95. 不同的二叉搜索树 II
给你一个整数 n ,请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。
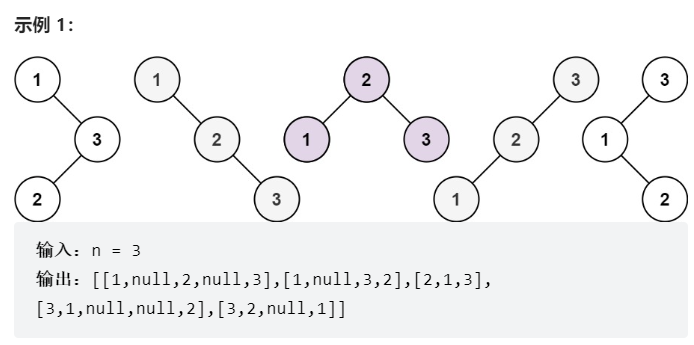
class Solution {
public List<TreeNode> generateTrees(int n) {
if(n==0) return new LinkedList<>();
// 构造闭区间 [1, n] 组成的 BST
return build(1,n);
}
/* 构造闭区间 [lo, hi] 组成的 BST */
private List<TreeNode> build(int lo, int hi){
List<TreeNode> res = new LinkedList<>();
// base case
if(lo > hi){
res.add(null);
return res;
}
// 1、穷举 root 节点的所有可能
for (int i = lo; i <= hi; i++) {
// 2、递归构造出左右子树的所有合法 BST
List<TreeNode> leftTree = build(lo, i - 1);
List<TreeNode> rightTree = build(i + 1, hi);
// 3、给 root 节点穷举所有左右子树的组合
for(TreeNode left : leftTree){
for(TreeNode right : rightTree){
// i 作为根节点 root 的值
TreeNode root = new TreeNode(i);
root.left = left;
root.right = right;
res.add(root);
}
}
}
return res;
}
}
–end–

![[测试猿课堂]接口自动化软件测试Requests模块从0到精通 一篇搞定](https://img-blog.csdnimg.cn/img_convert/09f102e2b01929c07082ec7bc620b04a.jpeg)







![[Java]面向对象高级篇](https://img-blog.csdnimg.cn/fdacd94b6b564c7d8a7c7a8df5f933e1.png)




