Lesson 10.1 超参数优化与枚举网格的理论极限和随机网格搜索 RandomSearchCV

news2024/10/6 8:38:29

文章目录

  • 一、超参数优化与枚举网格的理论极限
    • 1. 超参数优化 HPO（HyperParameter Optimization）
    • 2. 网格搜索的理论极限与缺点
    • 3. 建立 benchmark：随机森林中枚举网格搜索的结果
  • 二、随机网格搜索 RandomizedSearchCV
    • 1. 基本原理
    • 2. 随机网格搜索的实现
    • 3. 相同的全域参数空间
    • 4. 随机网格搜索的理论极限
    • 5. 更大/更密集的全域空间
    • 6. 连续型的参数空间

  • 首先，导入我们需要的库。
import numpy as np
import pandas as pd
import sklearn
import matplotlib as mlp
import matplotlib.pyplot as plt
import seaborn as sns
import time
import re, pip, conda

一、超参数优化与枚举网格的理论极限

1. 超参数优化 HPO（HyperParameter Optimization）

  • 每一个机器学习算法都会有超参数，而超参数的设置很大程度上影响了算法实际的使用效果，因此调参是机器学习算法工程师最为基础和重要的任务。
  • 现代机器学习与深度学习算法的超参数量众多，不仅实现方法异常灵活、算法性能也受到更多的参数的复合影响，因此当人工智能浪潮来临时，可以自动选择超参数的超参数优化 HPO 领域也迎来了新一轮爆发。
  • 在算法的世界中，我们渴望一切流程最终都走向完美自动化，专门研究机器学习自动化的学科被称为 AutoML，而超参数自动优化是 AutoML 中最成熟、最深入、也是最知名的方向。
  • 理论上来说，当算力与数据足够时，HPO 的性能一定是超过人类的。HPO 能够降低人为工作量，并且 HPO 得出的结果比认为搜索的复现可能性更高，所以 HPO 可以极大程度提升科学研究的复现性和公平性。当代超参数优化算法主要可以分为：
  • （1） 基于网格的各类搜索（Grid）。
  • （2） 基于贝叶斯优化的各类优化算法（Baysian）。
  • （3） 基于梯度的各类优化（Gradient-based）。
  • （4） 基于种群的各类优化（进化算法，遗传算法等）。
  • 其中，各类网格搜索方法与基于贝叶斯的优化方法是最为盛行的，贝叶斯优化方法甚至可以被称为是当代超参数优化中的 SOTA 模型。这些模型对于复杂集成算法的调整有极大的作用与意义。

2. 网格搜索的理论极限与缺点

  • 在所有超参数优化的算法当中，枚举网格搜索是最为基础和经典的方法。在搜索开始之前，我们需要人工将每个超参数的备选值一一列出，多个不同超参数的不同取值之间排列组合，最终将组成一个参数空间（parameter space）。
  • 枚举网格搜索算法会将这个参数空间当中所有的参数组合带入模型进行训练，最终选出泛化能力最强的组合作为模型的最终超参数。
  • 对网格搜索而言，如果参数空间中的某一个点指向了损失函数真正的最小值，那枚举网格搜索时一定能够捕捉到该最小值以及对应的参数（相对的，假如参数空间中没有任意一点指向损失函数真正的最小值，那网格搜索就一定无法找到最小值对应的参数组合）。
  • 参数空间越大、越密，参数空间中的组合刚好覆盖损失函数最小值点的可能性就会越大。这是说，极端情况下，当参数空间穷尽了所有可能的取值时，网格搜索一定能够找到损失函数的最小值所对应的最优参数组合，且该参数组合的泛化能力一定是强于人工调参的。
  • 但是，参数空间越大，网格搜索所需的算力和时间也会越大，当参数维度上升时，网格搜索所需的计算量更是程指数级上升的。以随机森林为例：
  • 只有 1 个参数 n_estimators，备选范围是 [50,100,150,200,250,300]，需要建模 6 次。
  • 当我们增加参数 max_depth，且备选范围是 [2,3,4,5,6]，需要建模 30 次。
  • 当我们增加参数 min_sample_split，且备选范围为 [2,3,4,5]，需要建模 120 次。
  • 同时，参数优化的目标是找出令模型泛化能力最强的组合，因此需要交叉验证来体现模型的泛化能力，假设交叉验证次数为 5，则三个参数就需要建模 600 次。
  • 在面对超参数众多、且超参数取值可能无限的人工神经网络、融合模型、集成模型时，伴随着数据和模型的复杂度提升，网格搜索所需要的时间会急剧增加，完成一次枚举网格搜索可能需要耗费几天几夜。

3. 建立 benchmark：随机森林中枚举网格搜索的结果

from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.model_selection import cross_validate, KFold, GridSearchCV

data = pd.read_csv(r"D:\Pythonwork\2021ML\PART 2 Ensembles\datasets\House Price\train_encode.csv",index_col=0)

X = data.iloc[:,:-1]
y = data.iloc[:,-1]

X.shape
#(1460, 80)

X.head()

y.describe() #RMSE

#参数空间
param_grid_simple = {"criterion": ["squared_error","poisson"]
                     , 'n_estimators': [*range(20,100,5)]
                     , 'max_depth': [*range(10,25,2)]
                     , "max_features": ["log2","sqrt",16,32,64,"auto"]
                     , "min_impurity_decrease": [*np.arange(0,5,10)]
                    }

#参数空间大小计算
2 * len([*range(20,100,5)]) * len([*range(10,25,2)]) * len(["log2","sqrt",16,32,64,"auto"]) * len([*np.arange(0,5,10)])
#1536

#直接使用循环计算
no_option = 1
for i in param_grid_simple:
    no_option *= len(param_grid_simple[i])

no_option
#1536

#模型，交叉验证，网格搜索
reg = RFR(random_state=1412,verbose=True,n_jobs=-1)
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
search = GridSearchCV(estimator=reg
                     ,param_grid=param_grid_simple
                     ,scoring = "neg_mean_squared_error"
                     ,verbose = True
                     ,cv = cv
                     ,n_jobs=-1)

#=====【TIME WARNING: 7mins】=====#
start = time.time()
search.fit(X,y)
print(time.time() - start)
Fitting 5 folds for each of 1536 candidates, totalling 7680 fits
#381.6039867401123

381.6039/60
#6.3600650000000005

search.best_estimator_
#RandomForestRegressor(max_depth=23, max_features=16, min_impurity_decrease=0,
#                      n_estimators=85, n_jobs=-1, random_state=1412,
#                      verbose=True)

abs(search.best_score_)**0.5
#29179.698261599166

#按最优参数重建模型，查看效果
ad_reg = RFR(n_estimators=85, max_depth=23, max_features=16, random_state=1412)

cv = KFold(n_splits=5,shuffle=True,random_state=1412)
result_post_adjusted = cross_validate(ad_reg,X,y,cv=cv,scoring="neg_mean_squared_error"
                          ,return_train_score=True
                          ,verbose=True

                          ,n_jobs=-1)

def RMSE(cvresult,key):
    return (abs(cvresult[key])**0.5).mean()

RMSE(result_post_adjusted,"train_score")
#11000.81099038192

RMSE(result_post_adjusted,"test_score")
#28572.070208366855
HPO方法默认参数网格搜索
搜索空间/全域空间-1536/1536
运行时间（分钟）-6.36
搜索最优（RMSE）30571.26629179.698
重建最优（RMSE）-28572.070
#打包成函数供后续使用
#评估指标RMSE
def RMSE(cvresult,key):
    return (abs(cvresult[key])**0.5).mean()
​
#计算参数空间大小
def count_space(param):
    no_option = 1
    for i in param_grid_simple:
        no_option *= len(param_grid_simple[i])
    print(no_option)
    
#在最优参数上进行重新建模验证结果
def rebuild_on_best_param(ad_reg):
    cv = KFold(n_splits=5,shuffle=True,random_state=1412)
    result_post_adjusted = cross_validate(ad_reg,X,y,cv=cv,scoring="neg_mean_squared_error"
                                          ,return_train_score=True
                                          ,verbose=True
                                          ,n_jobs=-1)
    print("训练RMSE:{:.3f}".format(RMSE(result_post_adjusted,"train_score")))
    print("测试RMSE:{:.3f}".format(RMSE(result_post_adjusted,"test_score")))

二、随机网格搜索 RandomizedSearchCV

1. 基本原理

  • 在讲解网格搜索时我们提到，伴随着数据和模型的复杂度提升，网格搜索所需要的时间急剧增加。以随机森林算法为例，如果使用过万的数据，搜索时间则会立刻上升好几个小时。因此，我们急需寻找到一种更加高效的超参数搜索方法。
  • 首先，当所使用的算法确定时，决定枚举网格搜索运算速度的因子一共有两个：
  • （1） 参数空间的大小：参数空间越大，需要建模的次数越多。
  • （2） 数据量的大小：数据量越大，每次建模时需要的算力和时间越多。
  • 因此，sklearn 中的网格搜索优化方法主要包括两类，其一是调整搜索空间，其二是调整每次训练的数据。其中，调整参数空间的具体方法，是放弃原本的搜索中必须使用的全域超参数空间，改为挑选出部分参数组合，构造超参数子空间，并只在子空间中进行搜索。
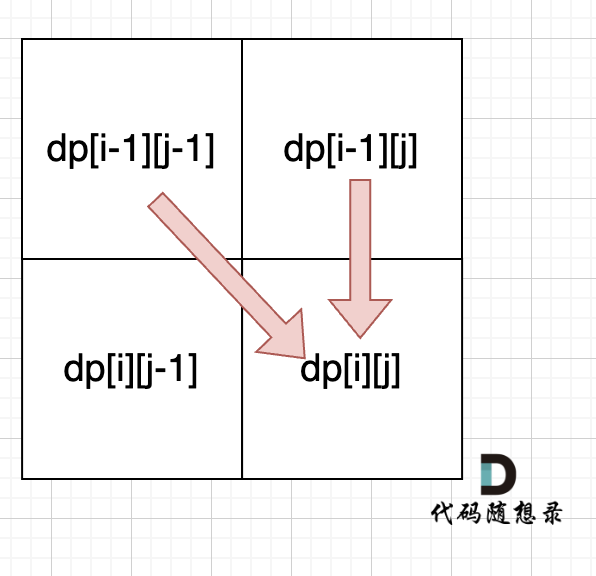
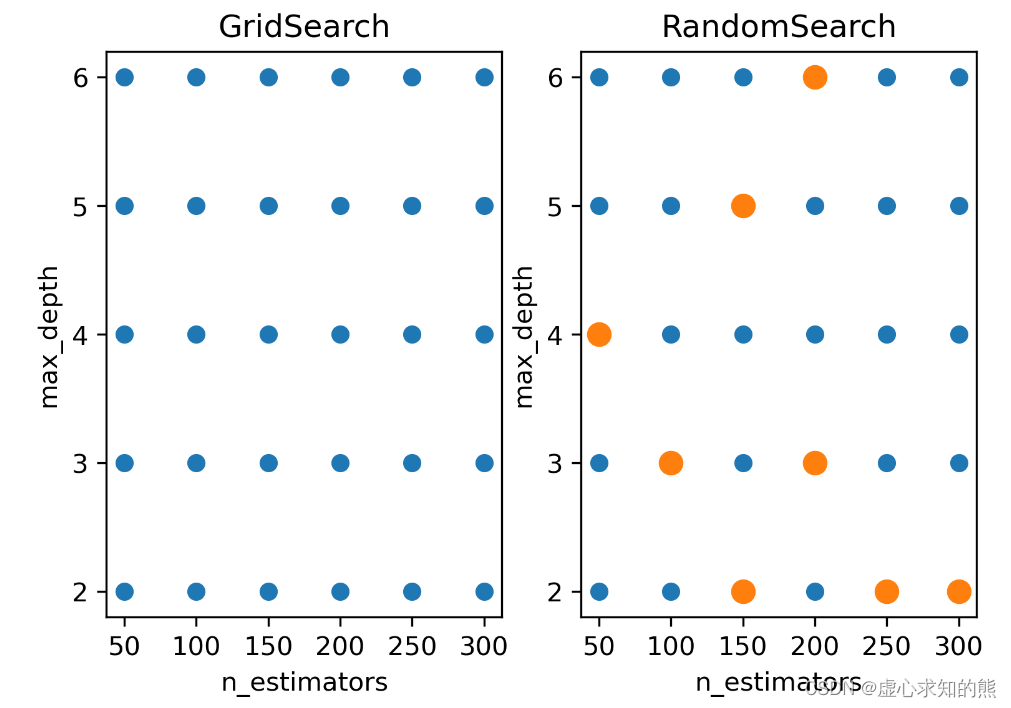
  • 以下图的二维空间为例，在这个 n_estimators 与 max_depth 共同组成的参数空间中，n_estimators 的取值假设为 [50,100,150,200,250,300]，max_depth 的取值假设为 [2,3,4,5,6]，则枚举网格搜索必须对 30 种参数组合都进行搜索。
  • 当我们调整搜索空间，我们可以只抽样出橙色的参数组合作为子空间，并只对橙色参数组合进行搜索。
fig, [ax1, ax2] = plt.subplots(1,2,dpi=300)
n_e_list = [*range(50,350,50)]
m_d_list = [*range(2,7)]
comb = pd.DataFrame([(n_estimators, max_depth) for n_estimators in n_e_list for max_depth in m_d_list])
​
ax1.scatter(comb.iloc[:,0],comb.iloc[:,1],cmap="Blues")
ax1.set_xticks([*range(50,350,50)])
ax1.set_yticks([*range(2,7)])
ax1.set_xlabel("n_estimators")
ax1.set_ylabel("max_depth")
ax1.set_title("GridSearch")
​
ax2.scatter(comb.iloc[:,0],comb.iloc[:,1],cmap="Blues")
ax2.scatter([50,250,200,200,300,100,150,150],[4,2,6,3,2,3,2,5],cmap="red",s=20,linewidths=5)
ax2.set_xticks([*range(50,350,50)])
ax2.set_yticks([*range(2,7)])
ax2.set_xlabel("n_estimators")
ax2.set_ylabel("max_depth")
ax2.set_title("RandomSearch");

在这里插入图片描述

  • 在 sklearn 中，随机抽取参数子空间并在子空间中进行搜索的方法叫做随机网格搜索 RandomizedSearchCV。
  • 由于搜索空间的缩小，需要枚举和对比的参数组的数量也对应减少，整体搜索耗时也将随之减少，因此：
  • 当设置相同的全域空间时，随机搜索的运算速度比枚举网格搜索快很多。
  • 当设置相同的训练次数时，随机搜索可以覆盖的空间比枚举网格搜索大很多。
  • 同时，绝妙的是，随机网格搜索得出的最小损失与枚举网格搜索得出的最小损失很接近。
  • 可以说，是提升了运算速度，又没有过多地伤害搜索的精度。
  • 不过，需要注意的是，随机网格搜索在实际运行时，并不是先抽样出子空间，再对子空间进行搜索，而是仿佛循环迭代一般，在这一次迭代中随机抽取 1 组参数进行建模，下一次迭代再随机抽取 1 组参数进行建模，由于这种随机抽样是不放回的，因此不会出现两次抽中同一组参数的问题。
  • 我们可以控制随机网格搜索的迭代次数，来控制整体被抽出的参数子空间的大小，这种做法往往被称为赋予随机网格搜索固定的计算量，当全部计算量被消耗完毕之后，随机网格搜索就停止。

2. 随机网格搜索的实现

from sklearn.model_selection import RandomizedSearchCV
  • 其函数语法模板如下：
class sklearn.model_selection.RandomizedSearchCV(estimator, param_distributions, *, n_iter=10, scoring=None, n_jobs=None, refit=True, cv=None, verbose=0, pre_dispatch='2*n_jobs', random_state=None, error_score=nan, return_train_score=False)
  • 全部参数解读如下，其中加粗的是随机网格搜索独有的参数：
NameDescription
estimator调参对象，某评估器
param_distributions全域参数空间，可以是字典或者字典构成的列表
n_iter迭代次数，迭代次数越多，抽取的子参数空间越大
scoring评估指标，支持同时输出多个参数
n_jobs设置工作时参与计算的线程数
refit挑选评估指标和最佳参数，在完整数据集上进行训练
cv交叉验证的折数
verbose输出工作日志形式
pre_dispatch多任务并行时任务划分数量
random_state随机数种子
error_score当网格搜索报错时返回结果，选择’raise’时将直接报错并中断训练过程，其他情况会显示警告信息后继续完成训练
return_train_score在交叉验证中是否显示训练集中参数得分
  • 我们依然借用之前在网格搜索上见过的 X 和 y，以及随机森林回归器，来实现随机网格搜索：
X.shape
#(1460, 80)

X.head()

y.describe()

3. 相同的全域参数空间

  • 我们先创造参数空间，也就是和使用与网格搜索时完全一致的空间，以便于进行对比操作。
param_grid_simple = {"criterion": ["squared_error","poisson"]
                     , 'n_estimators': [*range(20,100,5)]
                     , 'max_depth': [*range(10,25,2)]
                     , "max_features": ["log2","sqrt",16,32,64,"auto"]
                     , "min_impurity_decrease": [*np.arange(0,5,10)]
                    }
​
  • 然后建立回归器。进行交叉验证。
reg = RFR(random_state=1412,verbose=True,n_jobs=-1)
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
  • 计算全域参数空间大小，这是我们能够抽样的最大值。
count_space(param_grid_simple)
#1536
  • 进行定义随机搜索。
search = RandomizedSearchCV(estimator=reg
                            ,param_distributions=param_grid_simple
                            ,n_iter = 800 #子空间的大小是全域空间的一半左右
                            ,scoring = "neg_mean_squared_error"
                            ,verbose = True
                            ,cv = cv
                            ,random_state=1412
                            ,n_jobs=-1
                           )
  • 训练随机搜索评估器。
#=====【TIME WARNING: 5~10min】=====#
start = time.time()
search.fit(X,y)
print(time.time() - start)
#Fitting 5 folds for each of 800 candidates, totalling 4000 fits
#170.16785073280334

170.1678/60
#2.83613
  • 查看模型结果。
search.best_estimator_
#RandomForestRegressor(max_depth=24, max_features=16, min_impurity_decrease=0,
#                      n_estimators=85, n_jobs=-1, random_state=1412,
#                      verbose=True)

abs(search.best_score_)**0.5
#29251.284326350575
  • 根据最优参数重建模型。
ad_reg = RFR(max_depth=24, max_features=16, min_impurity_decrease=0,
                      n_estimators=85, n_jobs=-1, random_state=1412,
                      verbose=True)
rebuild_on_best_param(ad_reg)
#训练RMSE:11031.299
#测试RMSE:28639.969
HPO方法默认参数网格搜索随机搜索
搜索空间/全域空间-1536/1536800/1536
运行时间（分钟）-6.362.83(↓)
搜索最优（RMSE）30571.26629179.69829251.284
重建最优（RMSE）-28572.07028639.969(↑)
  • 很明显，在相同参数空间、相同模型的情况下，随机网格搜索的运算速度是普通网格搜索的一半，当然，这与子空间是全域空间的一半有很大的联系。
  • 由于随机搜索只是降低搜索的次数，并非影响搜索过程本身，因此其运行时间基本就等于n_iter/全域空间组合数 * 网格搜索的运行时间。

4. 随机网格搜索的理论极限

  • 在机器学习算法当中，有非常多通过随机来提升运算速度（比如 Kmeans，随机挑选样本构建簇心，小批量随机梯度下降，通过随机来减少每次迭代需要的样本）、或通过随机来提升模型效果的操作（比如随机森林，比如极度随机树）。
  • 两种随机背后的原理完全不同，而随机网格搜索属于前者，这一类机器学习方法总是伴随着“从某个全数据集/全域中进行抽样”的操作，而这种操作能够有效的根本原因在于：
  • （1）抽样出的子空间可以一定程度上反馈出全域空间的分布，且子空间相对越大（含有的参数组合数越多），子空间的分布越接近全域空间的分布。
  • （2） 当全域空间本身足够密集时，很小的子空间也能获得与全域空间相似的分布。
  • （3） 如果全域空间包括了理论上的损失函数最小值，那一个与全域空间分布高度相似的子空间很可能也包括损失函数的最小值，或包括非常接近最小值的一系列次小值。
  • 我们可以通过绘制图像来直观地呈现这些事实。许多在数学上比较抽象的概念都可以被可视化。在这里，我们借助 matplotlib 工具库 mplot3d 中的一组默认数据。
from mpl_toolkits.mplot3d import axes3d

p1, p2, MSE = axes3d.get_test_data(0.05)
  • 其中，get_test_data 巨头自动获取数据的功能，可以自动生成复合某一分布的数据。我们现在假设这一组数据中有两个参数，p1 与 p2，两个参数组成的参数组合对应着损失函数值 MSE。
  • 参数 0.05 是指参数空间中，点与点之间的距离。因此该数字越小，取出来的样本越多。
len(p1) #参数1的取值有120个
#120

len(p2) #参数2的取值也有120个
#120
  • 那么，现在参数空间当中一共有 120*120=14400 种组合，所以参数空间中一共有 14400 个点。
MSE.shape #损失函数值，总共14400个点
#(120, 120)
  • 随后，我们绘制 P1 与 P2 的参数空间，这是一个呈现出 14400 个点的密集空间。
plt.figure(dpi=300)
plt.scatter(p1,p2,s=0.2)
plt.xticks(fontsize=9)
plt.yticks(fontsize=9)

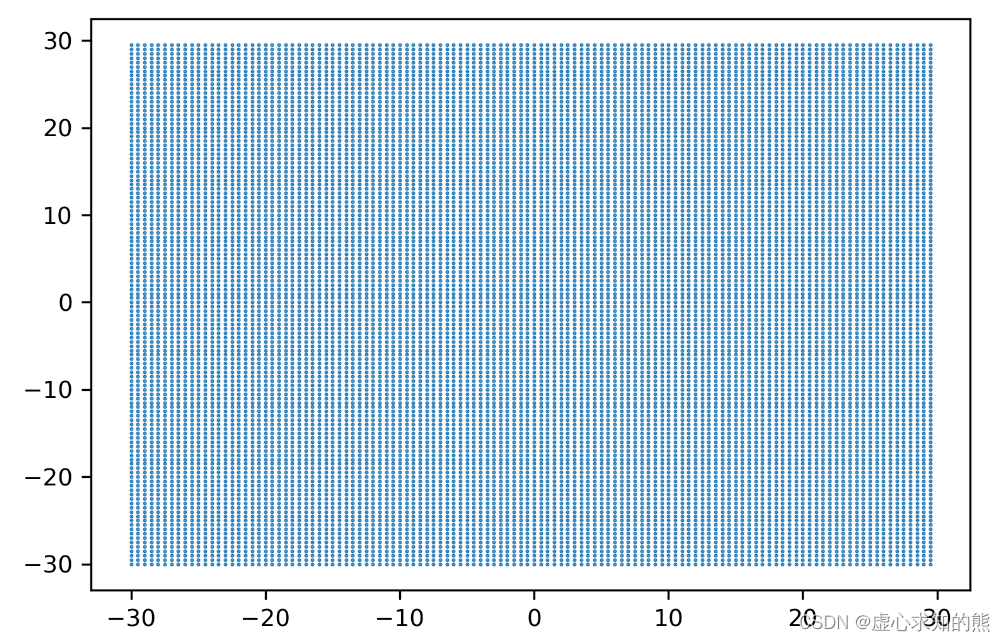
在这里插入图片描述

  • 参数与损失共同构建的函数。
p1, p2, MSE = axes3d.get_test_data(0.05)
plt.figure(dpi=300)
ax = plt.axes(projection="3d")
ax.plot_wireframe(p1,p2,MSE,rstride=2,cstride=2,linewidth=0.5)
ax.view_init(2, -15)
ax.zaxis.set_tick_params(labelsize=7)
ax.xaxis.set_tick_params(labelsize=7)
ax.yaxis.set_tick_params(labelsize=7)

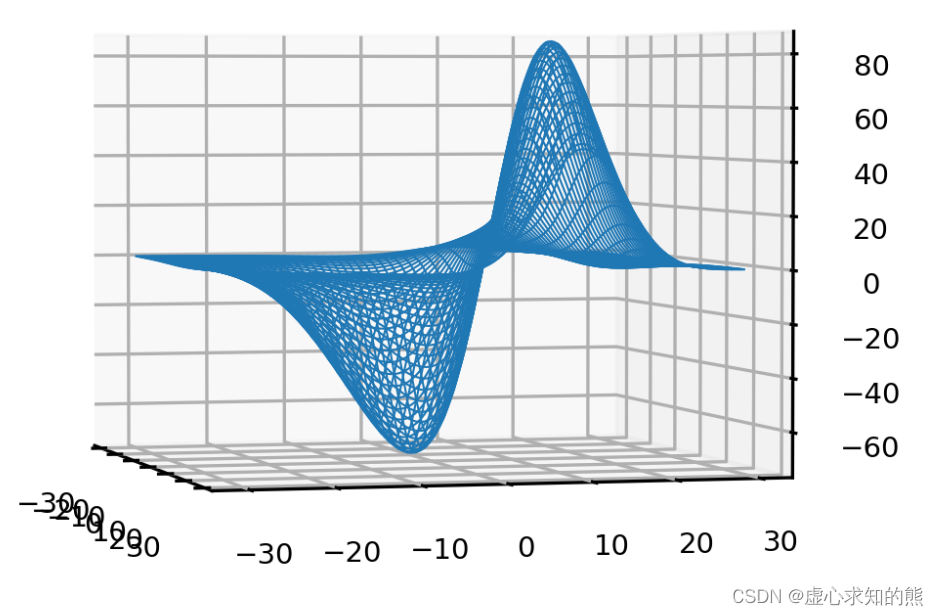
在这里插入图片描述

np.min(MSE) #整个参数空间中，可获得的MSE最小值是-73.39
#-73.39620971601681
  • 现在，我们从该空间上抽取子空间。
MSE.shape
#(120, 120)
  • 我们从空间中抽取 n 个组合，n 越大子空间越大。现在总共有 14400 个组合，对被抽中的点来说，损失函数的值就是 MSE，对没有抽中的点来说，损失函数值是空值。
  • 因此，我们只需要找出没有抽中的点，并让它的损失函数值 MSE 为空就可以了。从 0~14400 中生成（14400-n）个随机数，形成没有被抽到子空间中的点的索引。
n = 100
unsampled = np.random.randint(0,14400,14400-n)​
p1, p2, MSE = axes3d.get_test_data(0.05)
  • 拉平 MSE，并将所有没抽中的点的损失函数变为空值。
MSE = MSE.ravel()
MSE[unsampled] = np.nan
MSE = MSE.reshape((120,120))
  • 设置完毕空值后，记得把 MSE 恢复成原来的结构，否则绘图报错。
#参数与损失共同构建的函数
plt.figure(dpi=300)
ax = plt.axes(projection="3d")
ax.view_init(2, -15)
ax.plot_wireframe(p1,p2,MSE,rstride=2,cstride=2,linewidth=0.5)
ax.zaxis.set_tick_params(labelsize=7)
ax.xaxis.set_tick_params(labelsize=7)
ax.yaxis.set_tick_params(labelsize=7)
  • 求出当前损失函数上的最小值，注意此时因为 MSE 中含有了空值，因此要先排除空值影响，否则 min 函数会返回空值。
MSE = MSE.ravel().tolist()
MSE = [x for x in MSE if str(x) != 'nan']
print(np.min(MSE))
#-73.24243733589367

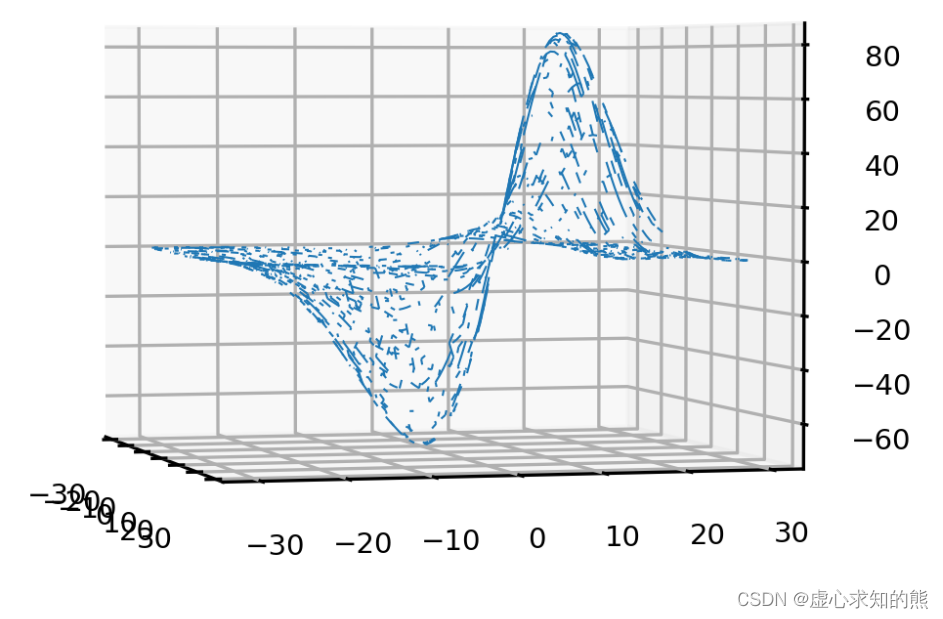
在这里插入图片描述

  • 我们可以在图像上验证如下事实：
  • （1） 抽样出的子空间可以一定程度上反馈出全域空间的分布，且子空间相对越大（含有的参数组合数越多），子空间的分布越接近全域空间的分布。
  • （2） 当全域空间本身足够密集时，很小的子空间也能获得与全域空间相似的分布。
  • （3） 如果全域空间包括了理论上的损失函数最小值，那一个与全域空间分布高度相似的子空间很可能也包括损失函数的最小值，或包括非常接近最小值的一系列次小值。
  • 因此，只要子空间足够大，随机网格搜索的效果一定是高度逼近枚举网格搜索的。在全域参数空间固定时，随机网格搜索可以在效率与精度之间做权衡。子空间越大，精度越高，子空间越小，效率越高。

5. 更大/更密集的全域空间

  • 不过，由于随机网格搜索计算更快，所以在相同计算资源的前提下，我们可以对随机网格搜索使用更大的全域空间，因此随机搜索可能得到比网格搜索更好的效果。
  • 我们可以创造参数空间 ，从而让整体参数空间变得更密。
param_grid_simple = {'n_estimators': [*range(80,100,1)]
                     , 'max_depth': [*range(10,25,1)]
                     , "max_features": [*range(10,20,1)]
                     , "min_impurity_decrease": [*np.arange(0,5,10)]
                    }
  • 计算全域参数空间大小，这是我们能够抽样的最大值。
count_space(param_grid_simple)
#3000
  • 建立回归器，进行交叉验证。
reg = RFR(random_state=1412,verbose=True,n_jobs=-1)
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
  • 定义随机搜索。
search = RandomizedSearchCV(estimator=reg
                            ,param_distributions=param_grid_simple
                            ,n_iter = 1536 #使用与枚举网格搜索类似的拟合次数
                            ,scoring = "neg_mean_squared_error"
                            ,verbose = True
                            ,cv = cv
                            ,random_state=1412
                            ,n_jobs=-1)
  • 训练随机搜索评估器。
start = time.time()
search.fit(X,y)
end = time.time() - start
print(end/60)
#Fitting 5 folds for each of 1536 candidates, totalling 7680 fits
#3.8464645385742187
  • 查看最佳评估器。
search.best_estimator_
RandomForestRegressor(max_depth=22, max_features=14, min_impurity_decrease=0,
                      n_estimators=89, n_jobs=-1, random_state=1412,
                      verbose=True)
  • 查看最终评估指标。
abs(search.best_score_)**0.5
#29012.90569846546

rebuild_on_best_param(search.best_estimator_)
#训练RMSE:11208.818
#测试RMSE:28346.673
HPO方法默认参数网格搜索随机搜索随机搜索
(大空间)
搜索空间/全域空间-1536/1536800/15361536/3000
运行时间（分钟）-6.362.83(↓)3.86(↓)
搜索最优（RMSE）30571.26629179.69829251.28429012.905(↓)
重建最优（RMSE）-28572.07028639.969(↑)28346.673(↓)
  • 可以发现，当全域参数空间增大之后，随即网格搜索可以使用与小空间上的网格搜索相似或更少的时间，来探索更密集/更大的空间，从而获得更好的结果。除了可以容忍更大的参数空间之外，随机网格搜索还可以接受连续性变量作为参数空间的输入。

6. 连续型的参数空间

  • 对于网格搜索来说，参数空间中的点是分布均匀、间隔一致的，因为网格搜索无法从某种“分布”中提取数据，只能使用组合好的参数组合点，而随机搜索却可以接受分”作为输入。
  • 如上图所示，对于网格搜索来说，损失函数的最低点很不幸的、位于两组参数之间，在这种情况下，枚举网格搜索是 100% 不可能找到最小值的。但对于随机网格搜索来说，由于是一段分布上随机选择参数点，因此在同样的参数空间中，取到更好的值的可能性更大。
import scipy #使用scipy来帮助我们建立分布

scipy.stats.uniform(loc=1,scale=100)
#<scipy.stats._distn_infrastructure.rv_frozen at 0x137a147d7c0>
  • uniform 是均匀分布，默认生成 [0,1] 之间的数字，可以使用 loc 来调整起点，scale 来调整终点。我们还可以选择其他的分布，比如指数分布 expon, gamma 分布, 或者是 randint。注意 scipy 这里并不是像 np.linspace() 一样生成一段离散的数字，而是直接生成一个分布对象。
  • 并且，我们并没有在分布对象中指定尺寸，也就是说，在这段分布上究竟要取几个随机的参数备选值，是由随机搜索自己决定的。理论上来说，我们给出的 n_iter 越大，任意参数的分布上可能被取到的点就越多。因此，当参数空间中包含某个分布的时候，我们无法估计全域参数空间的大小。
  • 在之前调整随机森林的时候，我们给出的所有参数都是只能接纳正整数的参数，因此在这里我们可以使用 scipy.stats.randint，不过 randint 并不是严格意义上的连续分布。
  • 严格来说，连续型搜索更适用于学习率，C，alpha 这样的参数（无上限，以浮点数为主），随机森林的参数中最接近这个定义的是 min_impurity_decrease，表示决策树在分枝是可以容忍的最小的不纯度下降量。我们借着这个参数，使用均匀分布来进行搜索试试看。
param_grid_simple = {'n_estimators': [*range(80,100,1)]
                     , 'max_depth': [*range(10,25,1)]
                     , "max_features": [*range(10,20,1)]
                     , "min_impurity_decrease": scipy.stats.uniform(0,50)
                    }

#建立回归器、交叉验证
reg = RFR(random_state=1412,verbose=True,n_jobs=12)
cv = KFold(n_splits=5,shuffle=True,random_state=1412)
​
#定义随机搜索
search = RandomizedSearchCV(estimator=reg
                            ,param_distributions=param_grid_simple
                            ,n_iter = 1536 #还是使用1536这个搜索次数
                            ,scoring = "neg_mean_squared_error"
                            ,verbose = True
                            ,cv = cv
                            ,random_state=1412
                            ,n_jobs=12)

#训练随机搜索评估器
start = time.time()
search.fit(X,y)
end = time.time() - start
print(end/60)
#Fitting 5 folds for each of 1536 candidates, totalling 7680 fits
#3.921058924992879

#查看最佳评估器
search.best_estimator_
#RandomForestRegressor(max_depth=22, max_features=14,
#                      min_impurity_decrease=20.070367229896224, n_estimators=98,
#                      n_jobs=12, random_state=1412, verbose=True)

#查看最终评估指标
abs(search.best_score_)**0.5
#29148.381610182565

rebuild_on_best_param(search.best_estimator_)
#训练RMSE:11184.428
#测试RMSE:28495.682
HPO方法默认参数网格搜索随机搜索随机搜索
(大空间)		随机搜索
(连续型)
搜索空间/全域空间-1536/1536800/15361536/30001536/无限
运行时间（分钟）-6.362.83(↓)3.86(↓)3.92
搜索最优（RMSE）30571.26629179.69829251.28429012.905(↓)29148.381
重建最优（RMSE）-28572.07028639.969(↑)28346.673(↓)28495.682
  • 在本次搜索当中，由于我们之前已经知道最好的可能的 min_impurity_decrease 的值为 0，因此强行向更大的数拓展搜索空间可能会导致模型效果下降。不过在随机森林当中，min_impurity_decrease 是唯一可以使用分布进行搜索的参数，因此在这里我们就容忍了这部分表现上升。
  • 理论上来说，当枚举网格搜索所使用的全域参数空间足够大/足够密集时，枚举网格搜索的最优解是随机网格搜索的上限，因此理论上随机网格搜索不会得到比枚举网格搜索更好的结果。
  • 但现实中的问题是，由于枚举网格搜索的速度太慢，因此枚举网格搜索的全域参数空间往往无法设置得很大，也无法设置得很密集，因此网格搜索的结果很难接近理论上的最优值。当随机网格搜索将空间设置更大、更密集时，就可以捕获更广空间的分布，也自然就可能捕获到理论上的最优值了。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/424733.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

使用chatgpt实现微信聊天小程序(秒回复)，github开源(附带链接)

使用chatgpt实现微信聊天小程序(秒回复)，github开源(附带链接)

文章目录前言效果展示原理说明服务器端代码说明微信小程序代码说明代码链接总结前言 我在前一段时间突发奇想&#xff0c;就使用java来调用chatgpt的接口&#xff0c;然后写了一个简单小程序&#xff0c;也上了热榜第一&#xff0c;java调用chatgpt接口&#xff0c;实现专属于…
阅读更多...
select 排序qsort排序

select 排序qsort排序

目录 1.希尔排序的时间复杂度 3.有技巧的选择排序&#xff1a;堆排序 4.排序的种类 5.直接插入排序和冒泡排序 6.快速排序 7.希尔排序 堆排序 和快排的区别 8.为什么相遇位置一定比key小 9.快排的优化 11.快排递归写法的不足 12.快排的非递归解法 1.希尔排序的时间复杂…
阅读更多...
C++11新特性(上)

C++11新特性(上)

357089 文章目录1. 统一的列表初始化1.1 &#xff5b;&#xff5d;初始化1.2 std::initializer_list2. decltype3. 右值引用和移动语义3.1 左值引用和右值引用3.2 左值引用与右值引用比较3.3 右值引用使用场景和意义3.4 右值引用引用左值及更深入的使用场景3.5 完美转发4. 新的…
阅读更多...
“编程式 WebSocket” 实现简易 online QQ在线聊天项目

“编程式 WebSocket” 实现简易 online QQ在线聊天项目

目录 一、需求分析与演示 1.1、需求分析 1.2、效果演示 二、客户端、服务器开发 2.1、客户端开发 2.2、服务器开发 一、需求分析与演示 1.1、需求分析 需求&#xff1a;实现一个 online QQ在线聊天项目&#xff0c;当用户登录上自己的账号后&#xff0c;将会显示在线&…
阅读更多...
我用nodejs和electron实现了一个简单的聊天软件-----chat 开源

我用nodejs和electron实现了一个简单的聊天软件-----chat 开源

翎&#x1f3a5;项目演示地址 &#x1f517;https://www.bilibili.com/video/BV1Fg4y1u76d/ 希望观众老爷给个免费的三连支持一下新人up主 ♻️项目基本介绍 翎是基于electron(vue2)和nodejs实现的简单聊天软件,其中用websocket和http进行通讯传递,数据库使用了mysql数据库,…
阅读更多...
二进制插入与查找组成一个偶数最接近的两个素数

二进制插入与查找组成一个偶数最接近的两个素数

二进制插入 链接&#xff1a;二进制插入_牛客题霸_牛客网 (nowcoder.com) 描述&#xff1a;给定两个32位整数n和m&#xff0c;同时给定i和j&#xff0c;将m的二进制数位插入到n的二进制的第j到第i位,保证n的第j到第i位均为零&#xff0c;且m的二进制位数小于等于i-j1&#xff…
阅读更多...
Qt Quick - Popup

Qt Quick - Popup

Qt Quick - Popup使用总结一、概述二、Popup 的布局三、弹出分级四、弹出定位五、定制化一、概述 Popup是类似弹出式用户界面控件的基本类型。它可以与Window或ApplicationWindow一起使用。 import QtQuick.Window 2.2import QtQuick.Controls 2.12ApplicationWindow {id: win…
阅读更多...
力推美团企业版 美团究竟意欲何为？

力推美团企业版 美团究竟意欲何为？

已经拥有930万活跃商家的美团公司&#xff0c;正在充分整合自身的“供应链”优势&#xff0c;冲向B端市场。 3月31日&#xff0c;据36氪消息显示&#xff0c;美团将于近期正式上线面向To B市场的业务“美团企业版”&#xff0c;定位企业消费赛道。美团企业版会为企业客户提供消…
阅读更多...
ZeroTier 内网穿透

ZeroTier 内网穿透

ZeroTier 内网穿透 官网注册账号&#xff0c;创建自己的局域网段, 登录官网 创建网络&#xff1a; 点击创建好的网络&#xff0c;进入设置界面进行设置, 选择 public 模式,点击入设置页面 地址随便选择 说明没有设备链接 下载客户端 &#xff0c;下载 安装客户端&#xf…
阅读更多...
高级数据结构与算法 | 三元搜索树（Ternary Search Tree）

高级数据结构与算法 | 三元搜索树（Ternary Search Tree）

文章目录TernarySearchTree基本概念介绍原理插入查找删除代码实现TernarySearchTree 基本概念 介绍 Ternary Search Tree&#xff08;三元搜索树&#xff09;&#xff0c;它是由 Bentley 和 Sedgewick 在 1997 年提出的一种基于 Trie 的思想改良的一种数据结构&#xff0c;其…
阅读更多...
【GCU体验】基于PyTorch + GCU跑通ResNet50模型并测试GCU性能

【GCU体验】基于PyTorch + GCU跑通ResNet50模型并测试GCU性能

一、环境 地址&#xff1a;启智社区:https://openi.pcl.ac.cn/ 二、计算卡介绍 云燧T20是基于邃思2.0芯片打造的面向数据中心的第二代人工智能训练加速卡&#xff0c;具有模型覆盖面广、性能强、软件生态开放等特点&#xff0c;可支持多种人工智能训练场景。同时具备灵活的可…
阅读更多...
win10 64位 环境下安装CUDA 11.8和 cuDNN v8.6.0

win10 64位 环境下安装CUDA 11.8和 cuDNN v8.6.0

win10 64位 环境下安装CUDA 11.8和 cuDNN v8.6.0 1 安装 NVIDIA 显卡驱动程序 下载地址&#xff1a;http://www.nvidia.cn/Download/index.aspx?langcn ​​​​​​ 下载文件&#xff1a;531.41-desktop-win10-win11-64bit-international-nsd-dch-whql 选择适合自己电脑的显…
阅读更多...
DeepFM论文翻译

DeepFM论文翻译

1.摘要 为了最大化推荐系统的CTR&#xff0c;学习用户行为的复杂交叉特征很关键。 尽管有很大进步&#xff0c;现有的方法无论对低阶还是高阶的交叉特征&#xff0c;似乎还是有很强的bias, 或者需要专门的特征工程。 本文&#xff0c;我们证明了得出一个能强化高阶和低阶交叉特…
阅读更多...
前端实现自动化测试

前端实现自动化测试

什么是前端测试 我们经常说的单元测试其实只是前端测试的一种。前端测试分为单元测试&#xff0c;UI 测试&#xff0c;集成测试和端到端测试。 ● 单元测试&#xff1a;是指对软件中的最小可测试单元进行检查和验证&#xff0c;通常指的是独立测试单个函数。 ● UI 测试&#…
阅读更多...
2023美赛Y题二手帆船价格--成品论文、思路、数据、代码

2023美赛Y题二手帆船价格--成品论文、思路、数据、代码

2023美赛Y题二手帆船价格 第一时间在CSDN分享 最新进度在文章最下方卡片&#xff0c;加入获取一手资源&#xff1a;2023美赛Y题二手帆船价格–成品论文、思路、数据、代码 可以提供关于帆船特性的信息: BoatTrader (https://www.boattrader.com/):一个网站&#xff0c;允许您根…
阅读更多...
WindowsGUI自动化测试项目实战+辛酸过程+经验分享

WindowsGUI自动化测试项目实战+辛酸过程+经验分享

WindowsGUI自动化测试项目实战辛酸过程经验分享一、前言⚜ 起因⚜ 项目要求⚜ 预研过程⚜⚜ 框架选型⚜⚜ 关于UIaotumation框架⚜ 预研成果二、项目介绍&#x1f493; 测试对象&#x1f493; 技术栈&#x1f493; 项目框架说明三、项目展示&#x1f923; 界面实现效果&#x1…
阅读更多...
【深度学习】windows10环境配置详细教程

【深度学习】windows10环境配置详细教程

【深度学习】windows10环境配置详细教程 文章目录【深度学习】windows10环境配置详细教程Anaconda31.安装Anaconda32.卸载Anaconda33.修改Anaconda3安装虚拟环境的默认位置安装cuda/cudnn1.安装合适的CUDA2.安装对应的CUDNN3.卸载CUDA/CUDNNconda虚拟环境独立安装cuda/cudnn1.搭…
阅读更多...
随想录Day55--动态规划: 392.判断子序列 , 115.不同的子序列

随想录Day55--动态规划: 392.判断子序列 , 115.不同的子序列

392.判断子序列 思路 &#xff08;这道题也可以用双指针的思路来实现&#xff0c;时间复杂度也是O(n)&#xff09; 动态规划五部曲分析如下&#xff1a; 1.确定dp数组&#xff08;dp table&#xff09;以及下标的含义 dp[i][j] 表示以下标i-1为结尾的字符串s&#xff0c;和…
阅读更多...
基线配置管理在网络中的重要性

基线配置管理在网络中的重要性

在网络环境中&#xff0c;配置通常被认为具有不可估量的价值&#xff0c;因为设备配置的微小变化可以在几分钟内成就或破坏整个网络基础设施。 这些配置分为两部分&#xff1a;启动配置和运行配置。在网络设备中&#xff0c;默认情况下&#xff0c;第一个配置版本被视为运行和…
阅读更多...
el-input-number的精度问题

el-input-number的精度问题

前言 el-input-number 饿了么的数字输入框组件&#xff0c;在项目中听常用的。而这个组件比较常用的属性就是精度设置&#xff0c;给组件添加属性precision 。 其实吧&#xff0c;之前一直没怎么研究&#xff0c;保留几位小数就直接填几就好了&#xff0c;比如保留两位小数&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023