文章目录
- TernarySearchTree
- 基本概念
- 介绍
- 原理
- 插入
- 查找
- 删除
- 代码实现
TernarySearchTree
基本概念
介绍
Ternary Search Tree(三元搜索树),它是由 Bentley 和 Sedgewick 在 1997 年提出的一种基于 Trie 的思想改良的一种数据结构,其目的在于优化 Trie 在大规模数据集下的时间、空间开销。
那么 TST 主要在哪几个方面优化呢?
- 子节点数:在 Trie 中,每一个节点都需要存储一个子节点指针数组,这个数组需要包含所有可能出现的字符,这就导致 Trie 的空间占用非常大,而在 TST 中,仅需要保留三个子节点指针。
- 字典序排列:在 Trie 中,查找时需要沿着树一直向下遍历,查询效率相对较低,而 TST 按照字典序对节点进行来排列,查找中可以依据该特点进行优化(例如使用二分查找)。
Trie 通常适用于少量字符串匹配、前缀匹配等场景,而 TST 主要应用于大量字符串查询的场景,例如搜索引擎、代码检查、自动补全。
原理
TST 的核心原理非常简单,与二叉树不同,TST 每个节点都存储着三个指向子节点的指针,这些子节点代表着查询字符串与该节点比较的结果,即:
- 当前节点的字符小于等于查询字符串的对应字符,则搜索左子树。
- 当前节点的字符大于等于查询字符串的对应字符,则搜索右子树。
- 当前节点的字符等于等于查询字符串的对应字符,则搜索中子树。
插入
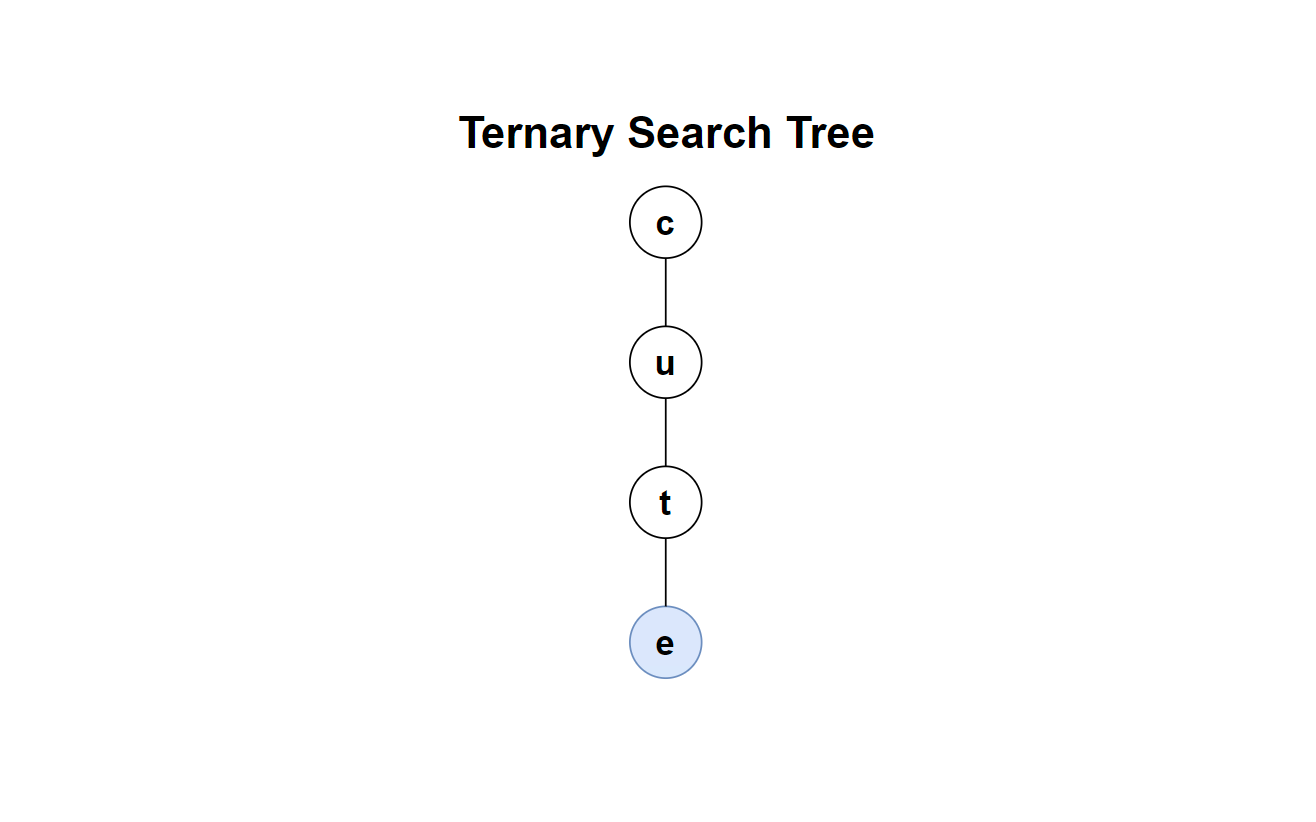
首先,往一个空树中插入一个字符串 cute。
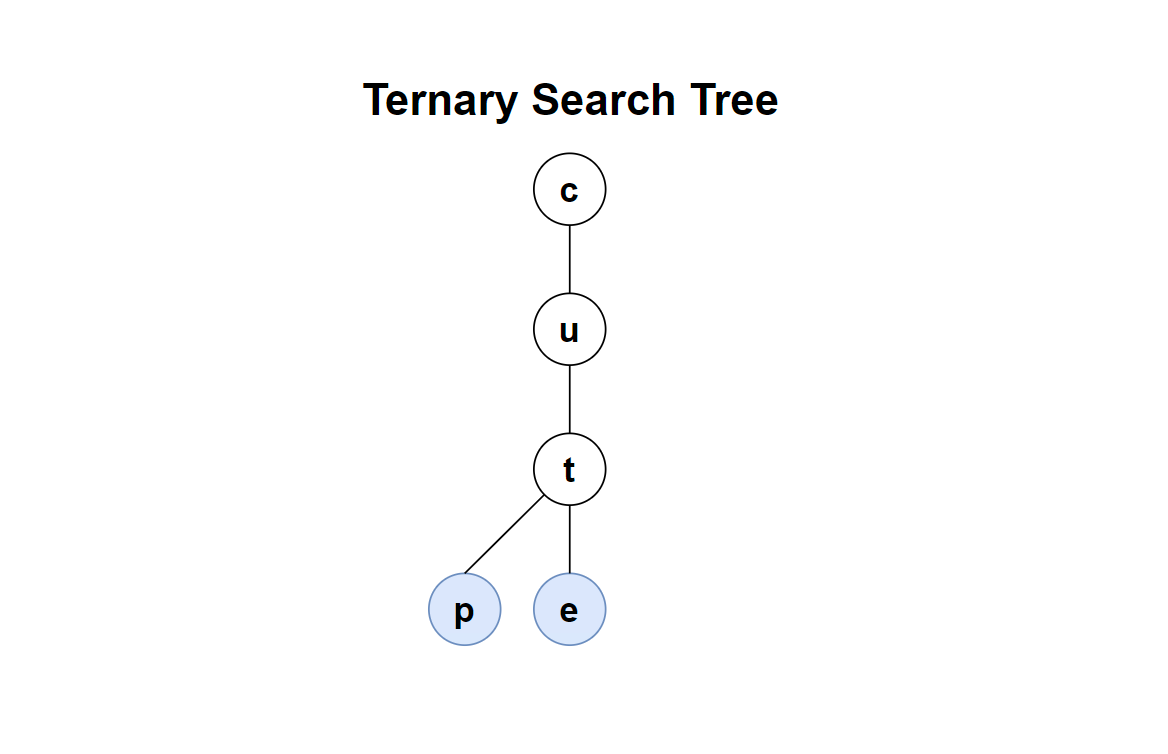
接着,插入字符串 cup,此时对比字符 c、u 都相同,进入其中间节点,到了 t 时,由于 p 比 t 小,则将 p 插入到 t 的左子树。

接着,插入一个字符串 he,由于 h 比 c 大,此时插入到 c 的右子树。
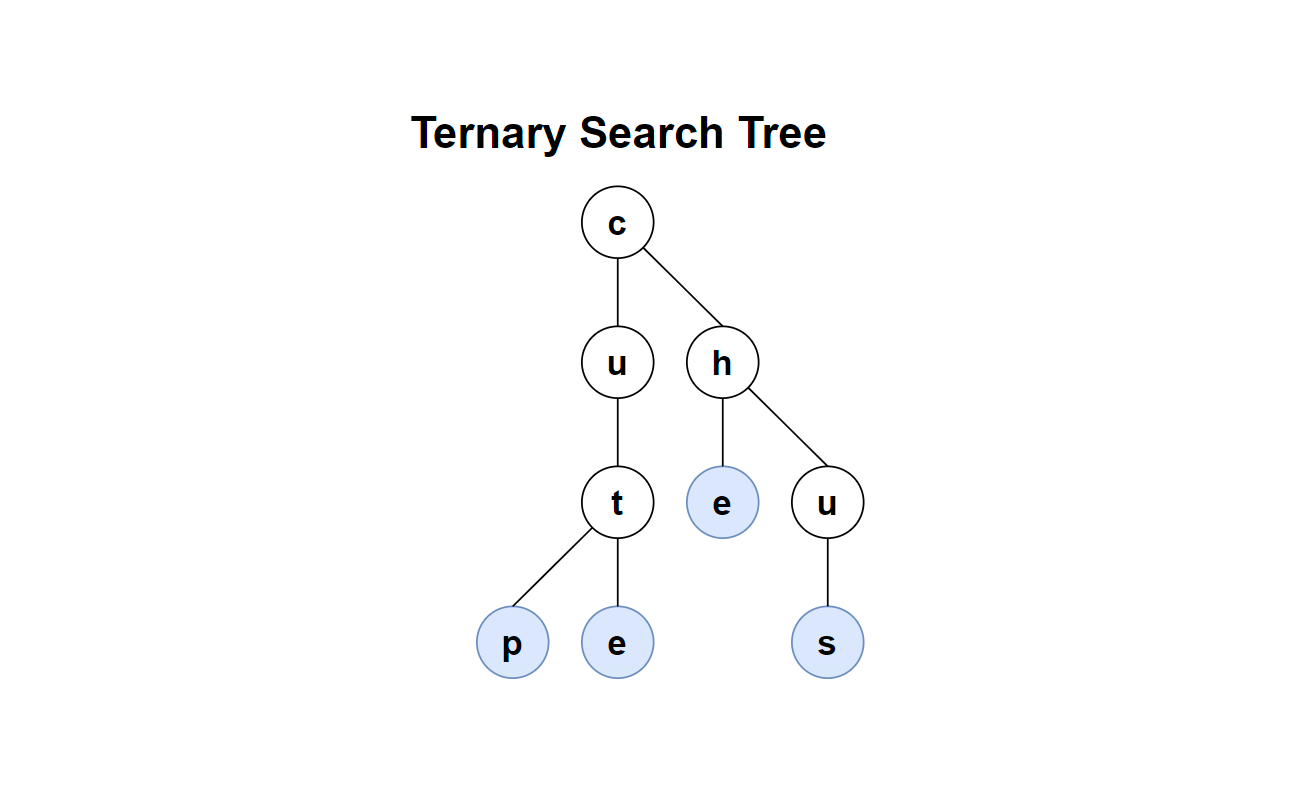
接着,插入一个字符串 us,由于 u 比 c 大,进入其右子树。接着对比 h,仍然比它大,此时将 u 插入其右子树。
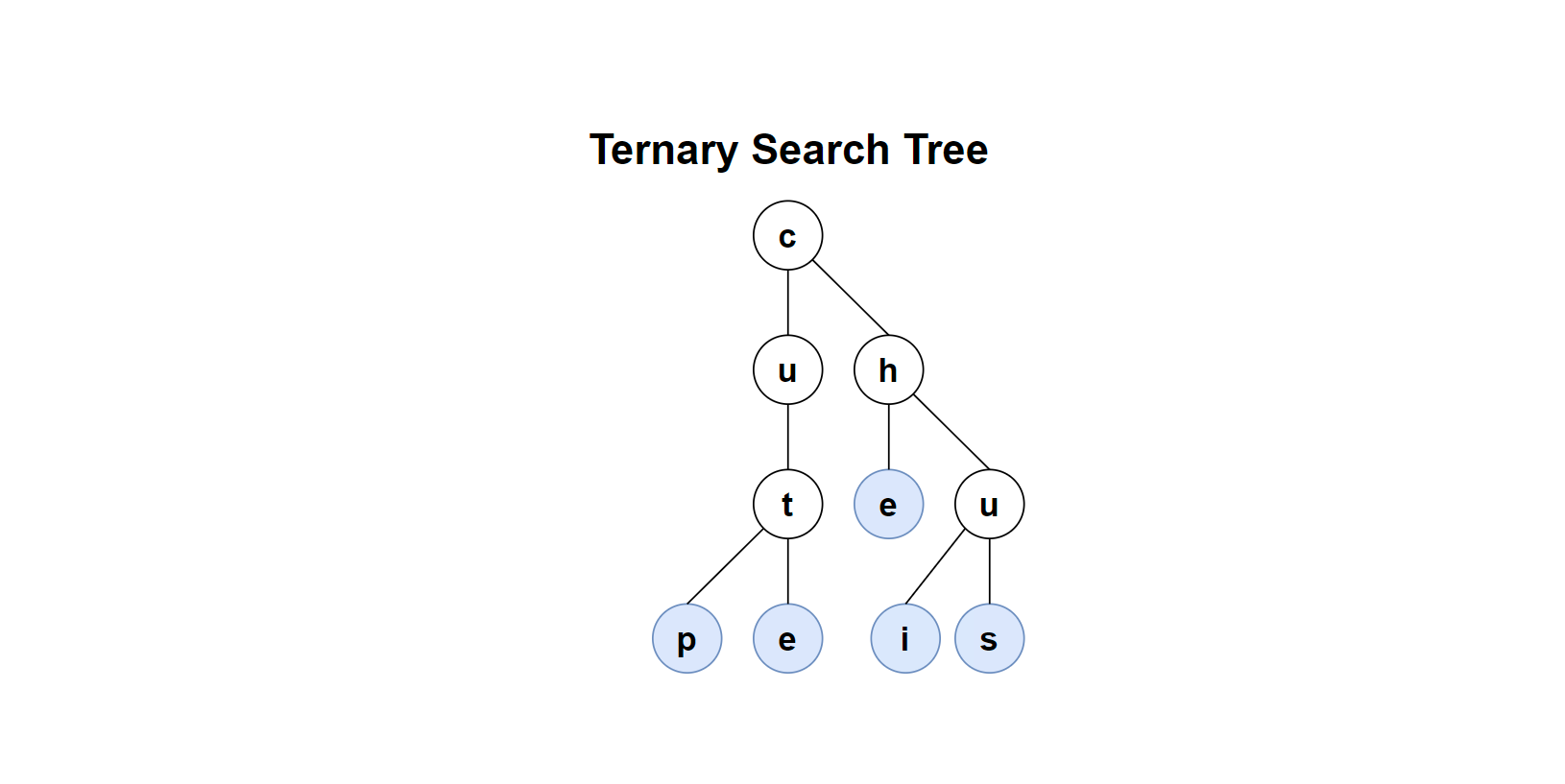
插入一个 i,由于 i 比 c 大,进入其右子树。对比 h,仍然比它大,进入其左子树。对于 u,此时其比 u 小,插入左子树。
查找
接着来举几个查找的例子。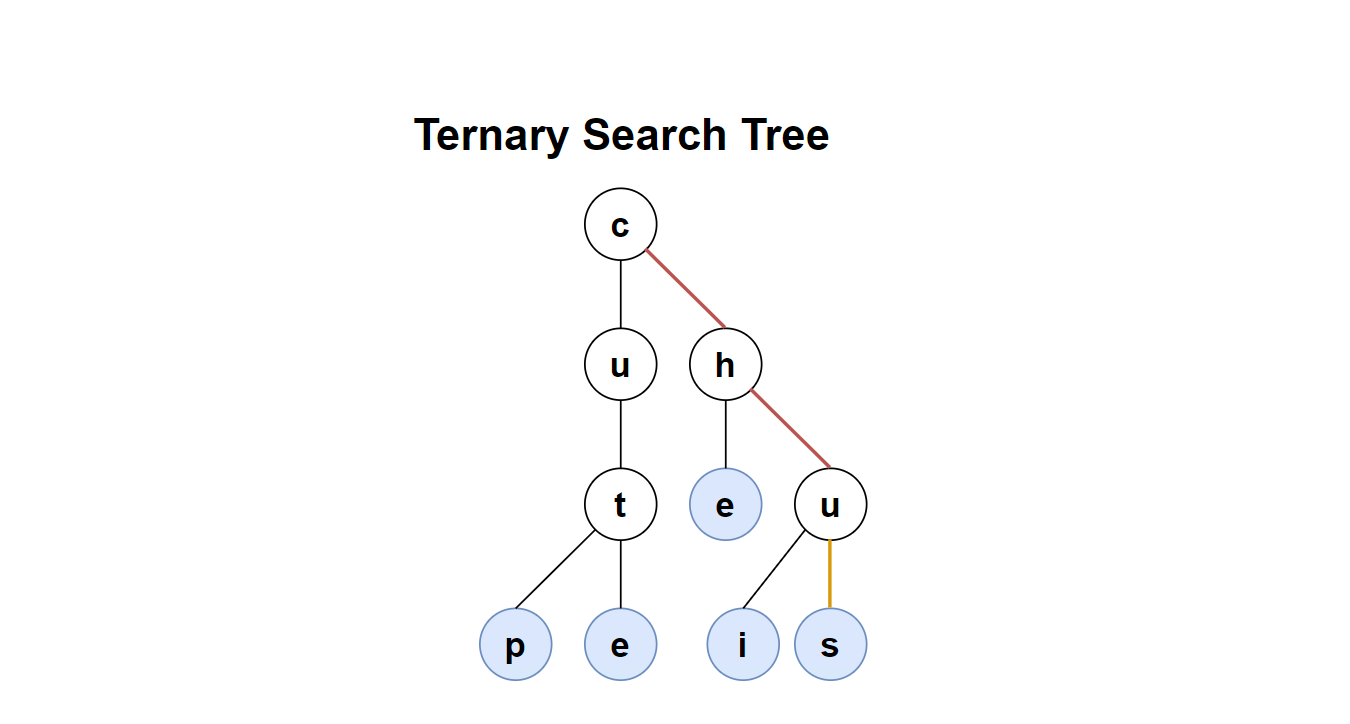
首先我们需要查找字符串 us 在不在树中,流程如下:
- u > c,进入其右子树。
- u > h,进入其右子树。
- u == u,进入其中子树。
- s == s,此时已到达叶子节点,且 us 刚好被标记为一个单词,查询成功。
删除
删除为插入的对称操作,只需要将最终找到的节点标记为 false 即可,如果是叶子节点则将其删除,这里就不过多赘述。
代码实现
TST 的原理上面已经讲过了,非常简单,这里就不过多介绍了,实现代码如下:
//
// Created by orekilee on 2023/4/8.
//
#ifndef TERNARY_SEARCH_TREE
#define TERNARY_SEARCH_TREE
#include <string>
#include <memory>
using namespace std;
class TernarySearchTreeNode {
public:
explicit TernarySearchTreeNode(char ch) :data(ch), is_end(false), left(nullptr), right(nullptr), mid(nullptr) {}
char data;
bool is_end;
shared_ptr<TernarySearchTreeNode> left;
shared_ptr<TernarySearchTreeNode> right;
shared_ptr<TernarySearchTreeNode> mid;
};
class TernarySearchTree {
public:
TernarySearchTree() :root(make_shared<TernarySearchTreeNode>('\0')) {};
virtual ~TernarySearchTree() = default;
TernarySearchTree(const TernarySearchTree &) = delete;
TernarySearchTree &operator=(const TernarySearchTree &) = delete;
bool search(const string &str) {
if (str.empty()) {
return root->is_end;
}
return search_helper(root, str, 0);
}
void insert(const string &str) {
if (str.empty()) {
root->is_end = true;
}
insert_helper(root, str, 0);
}
void erase(const string &str) {
if (str.empty()) {
root->is_end = false;
}
erase_helper(root, str, 0);
}
private:
bool search_helper(shared_ptr<TernarySearchTreeNode> node, const string &str, int index) {
if (node == nullptr) {
return false;
}
//如果比当前字符小,则去左节点,如果大则去右节点,如果相同则去中间节点
if (node->data > str[index]) {
return search_helper(node->left, str, index);
} else if (node->data < str[index]) {
return search_helper(node->right, str, index);
} else {
//如果遍历完整个str,根据is_end判断是否成功查找
if (str.size() - 1 > index) {
return search_helper(node->mid, str, index + 1);
} else {
return node->is_end;
}
}
}
shared_ptr<TernarySearchTreeNode> insert_helper(shared_ptr<TernarySearchTreeNode> node, const string &str, int index) {
if (node == nullptr) {
node = make_shared<TernarySearchTreeNode>(str[index]);
}
if (node->data > str[index]) {
node->left = insert_helper(node->left, str, index);
} else if (node->data < str[index]) {
node->right = insert_helper(node->right, str, index);
} else {
if (str.size() - 1 > index) {
node->mid = insert_helper(node->mid, str, index + 1);
} else {
node->is_end = true;
}
}
return node;
}
shared_ptr<TernarySearchTreeNode> erase_helper(shared_ptr<TernarySearchTreeNode> node, const string &str, int index) {
if (node == nullptr) {
return nullptr;
}
if (node->data > str[index]) {
return erase_helper(node->left, str, index);
} else if (node->data < str[index]) {
return erase_helper(node->right, str, index);
} else {
if (str.size() - 1 > index) {
return erase_helper(node->mid, str, index + 1);
} else {
node->is_end = false;
}
}
// 如果是叶子节点,则直接删除。这里资源用智能指针管理,直接标记为空即可
if (!node->left && !node->right && !node->mid) {
node = nullptr;
}
return node;
}
shared_ptr<TernarySearchTreeNode> root;
};
#endif // TERNARY_SEARCH_TREE