倍增？最近公共祖先？——从定义到实现，帮你一步步吃掉它！

news2024/11/26 1:46:03

倍增？最近公共祖先？——从定义到实现，帮你一步步吃掉它！

一、倍增倍增——翻倍的增长

倍增是一种思想，实际上的操作就是通过不断翻倍来缩短我们的处理时间：

它可以把线性级别的处理优化到指数级。

举个栗子：

现在有8个格子，我想从第1个格子去到第6个格子，怎么做到呢？

未命名绘图.png

最简单的做法就是直接一格一格的走到6号格子里，确实很简单，但这样子处理需要走5个格子。

让我们来看看倍增是怎么处理的：

未命名绘图1.png

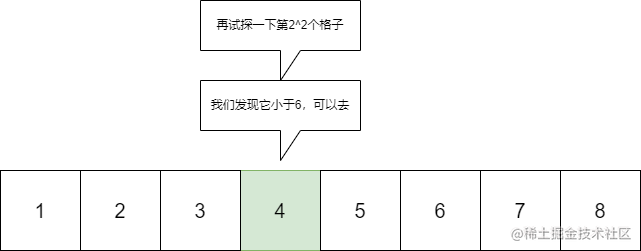
未命名绘图2.png

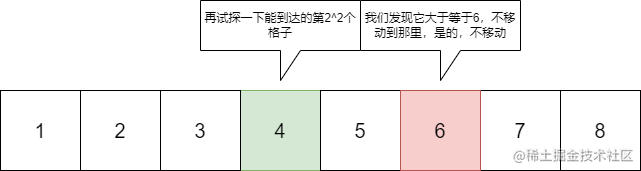
未命名绘图3.png

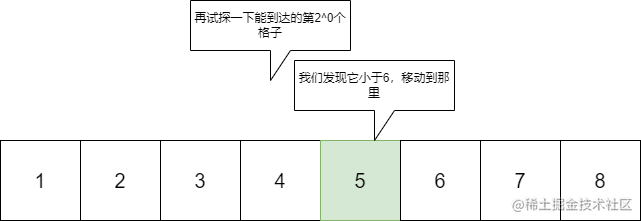
未命名绘图4.png

未命名绘图5.png

其实如此一看，这个倍增就跟二进制一样。

而且我们在倍增处理的过程中，进行了一种 “擦边球” 行为，即我们能去到目的地及其它之后的地方，但我们不去。

这样处理，到了最后我们就会离目的地无限接近，那么只要再一步，就可以到达目的地了。

事实上，我们在使用倍增来求最近公共祖先时也是类似这样的操作。

倍增的思想其实非常简单，但是重点是该如何去使用它。

接下来让我们看看——

二、公共祖先——这玩意还能公共吗

开个玩笑，这个所谓祖先和我们平日里说的”祖宗十八代“并不是同一个东西，就像我们在学习树状结构的时候称呼一个子节点的上面连着的节点是父节点一样，祖先节点也是类似的意思，不过父亲节点只有一个，而祖先节点则可以有很多个。

我们这里的公共祖先，通俗理解就是：

在同一颗树上，两个不同节点去往根节点时会经过的相同节点。

比如在这棵树中:

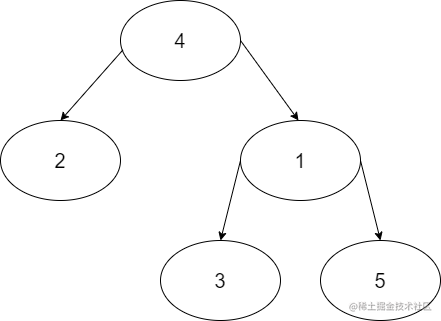
未命名绘图6.png

  • 节点3去往根节点4的路径是：3->1->4。
  • 节点5去往根节点4的路径是：5->1->4。

那么1和4都是它们经过的节点，我们就称这两个点是3和5的公共祖先。

最近公共祖先（LCA）就是离3和5最近的祖先节点，即节点1。

又比如2和3的最近公共祖先是4。

有些题目还会问两个相同节点的公共祖先，比如3和3，那么此时它们的公共祖先就是它们自己。 （？好奇怪的说法）

到了这里，公共祖先和倍增的理念我们都了解了，接下来进入我们的——

三、求祖先——喂你咋跪下了

上面一节在介绍公共祖先时，我们是怎么求出那颗树的3和5节点的公共祖先的？

未命名绘图6.png

我们是先从节点3走回根节点，然后再从节点5走回根节点，记录这两次的路径，路径上相同的节点就是它们的公共祖先，离他们最近的那个就是公共祖先了。

这个做法是没有问题的，确实可以求出正确的答案。但是缺点是太慢了！

我们看一看这样做的时间复杂度：

哪怕我们预处理并记录下所有节点到达根节点的路径，但是我们每次在询问两个点的最近公共祖先时，都要遍历一遍它俩的路径，这样单次询问的最坏复杂度是O(n)。

数据量小还好说，数据量大那是妥妥的死。所以我们要想办法去优化它。

这里我们采用的便是倍增法了。（别忘了我们的“擦边球”操作）

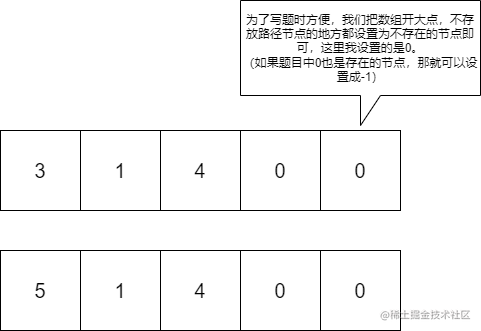
未命名绘图7.png
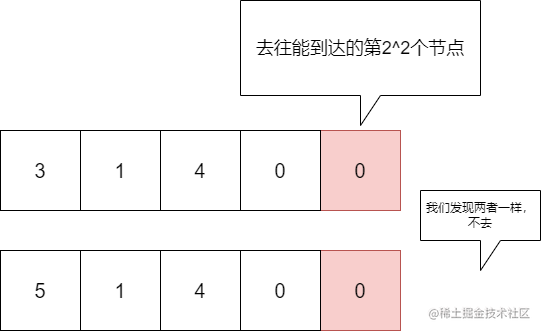
未命名绘图8.png
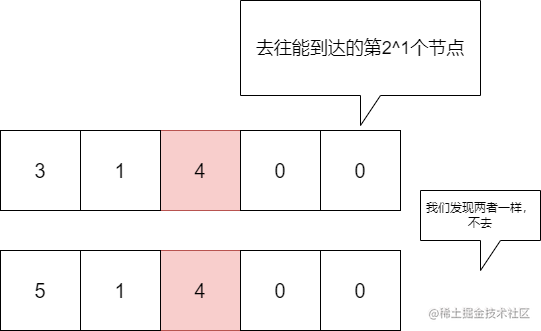
未命名绘图9.png
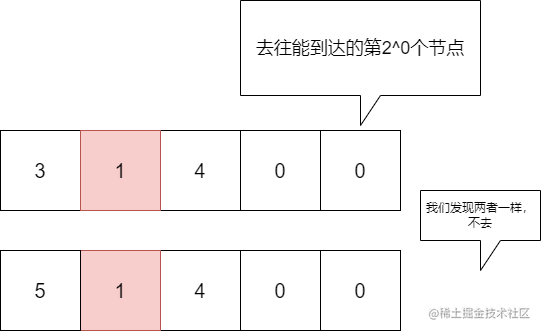
未命名绘图10.png
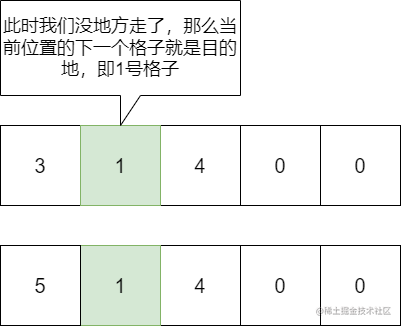
未命名绘图11.png

但是这样做其实有个问题，比如求节点2和节点3的公共祖先：

  • 节点2的路径是：2->4；
  • 节点3的路径是：3->1->4;

我们可以发现，如果此时我们一起移动，那么结果会是错误的，因为它们并没有同时相等的路径节点。

这是因为它俩到根节点的路径并不一样长，为了解决这个问题，我们应该保证节点2和3的剩余路径一样长。

即把节点3先移动到节点1。

为了方便处理这一情况，我们借用了树状结构中——“深度”的概念，即一个节点到根节点的距离。

  1. 用一个数组deep[]来维护节点的深度，初始设定deep[根节点]=1。
  2. 然后经过一遍dfs，在记录路径的同时也处理好每个节点的深度。
  3. 当我们求两个节点的最近公共祖先时，如果深度不一样，我们把深度较大的那个点先往上移动，直到两个节点的深度相等。
  4. 如果移动到深度相同时，我们发现这两个节点一样了，那么就说明这就是原来节点的最近公共祖先。

这就是通过倍增法求解最近公共祖先的做法了。

不过还有个之前被我们忽视的问题：我们该怎么记录路径？

如果每个节点都开个数组来存路径节点，占空间不说，实际操作起来也很慢。而且我们可以发现，并不是路径上所有的节点我们都需要，我们只需要每个节点的：第20个、第21个、第22个、……、第2k个祖先就行。

这里我们还是采用的倍增的思想：
  • 先准备一个祖先数组fa[N] [30]，fa[i] [j]表示节点i的第2^(j-1)个祖先节点。

比如这样一棵树：

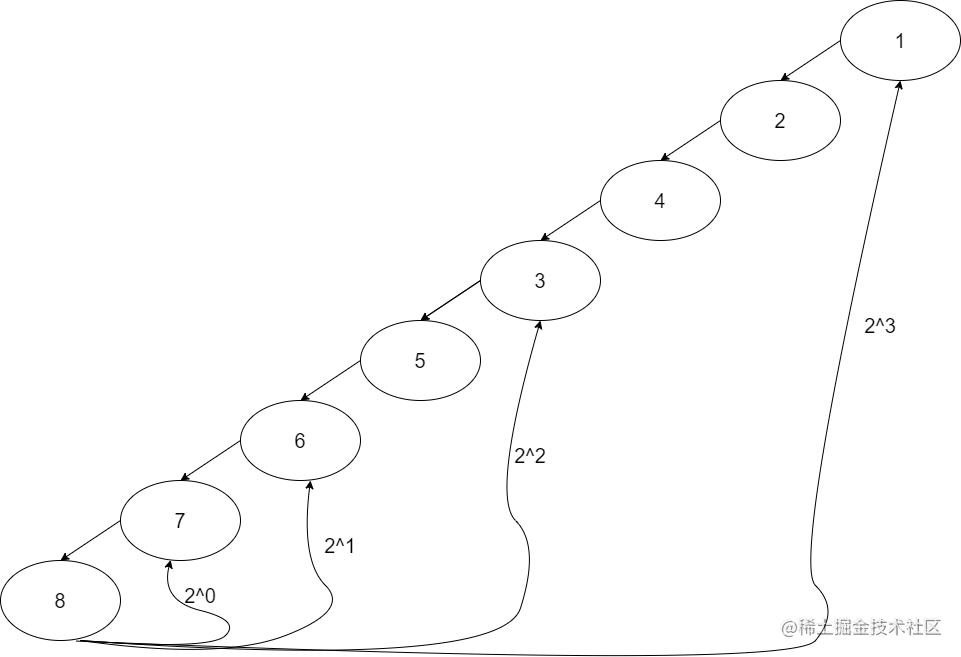
未命名绘图12.png

  • fa[8] [0]=7;
  • fa[8] [1]=6;
  • fa[8] [2]=3;
  • fa[8] [3]=1;

那么该如何推出这么一个公式呢？

我们可以发现：

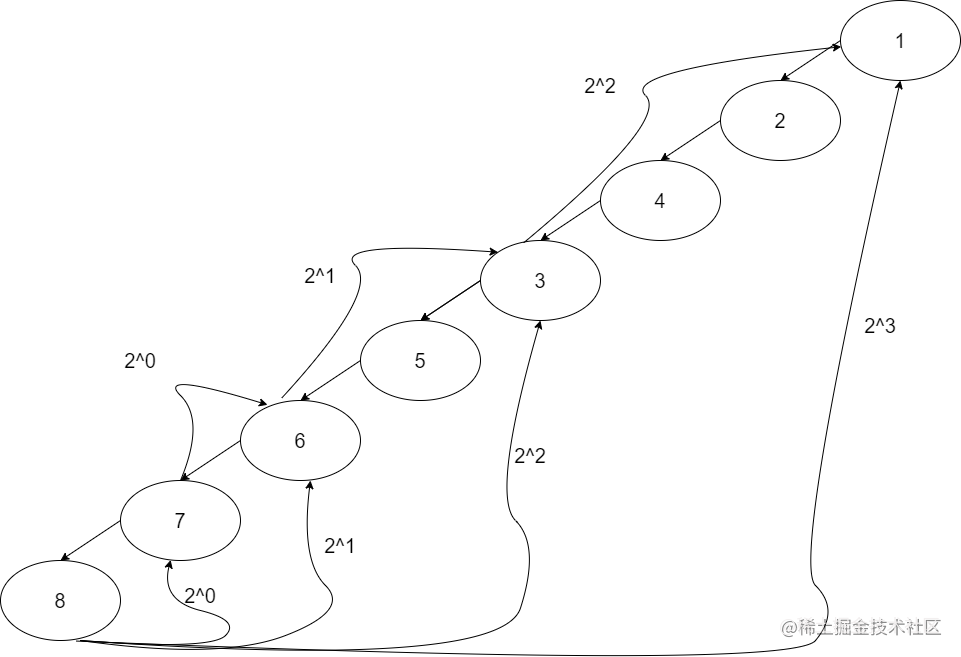
未命名绘图13.png

  1. fa[8] [0]其实就是8节点的父节点7。
  2. fa[8] [1]就是7的第2^0个节点。
  3. fa[8] [2]是fa[8] [1]的第2^1个节点。
  4. ……以此类推。

我们可以得到一个状态转移方程：

f a [ i ] [ k ] = f a [ ( f a [ i ] [ k − 1 ] ) ] [ k − 1 ] ; fa[ i ] [ k ] = fa[(fa[i] [k-1]) ] [ k-1 ]; fa[i][k]=fa[(fa[i][k−1])][k−1];

因为我们是不断计算i节点的第2^（1、2、3、……、k）个节点。可以知道k的上限为：

log ⁡ 2 d e e p [ i ] \log_2^{deep[i]} log2deep[i]​

一般来说k最大不会超过20。

这样我们就可以快速的记录下每一个点的祖先节点了。

至此，倍增思想求最近公共祖先的方法我们已经全部学会了，接下来让我们——

四、用代码实现

#include<iostream>
using namespace std;
#include<vector>
#include<algorithm>
#include<math.h>
#include<set>
#include <random>
#include<numeric>
#include<string>
#include<string.h>
#include<iterator>
#include<fstream>
#include<map>
#include<unordered_map>
#include<stack>
#include<list>
#include<queue>
#include<iomanip>
#include<bitset>
​
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
​
#define endl '\n'
#define int ll
#define PI acos(-1)
#define INF 0x3f3f3f3f
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll, ll>PII;
const int N = 5e5 + 50, MOD = 998244353;
​
//用二维数组模拟邻接表来存储树
vector<int>tree[N];
//deep记录每个节点的深度
//fa[i][k]表示节点i的第2^k个祖先
int deep[N], fa[N][32];
​
//dfs一遍求出所有点的深度和祖先节点
//x是当前节点，y是它的父节点
void dfs(int x, int y)
{
    //x的第2^0个节点就是父节点
    fa[x][0] = y;
    //逐步获取上面的祖先节点
    for (int i = 1; i < 20; i++)
    {
        fa[x][i] = fa[fa[x][i - 1]][i - 1];
    }
    //遍历和点x链接的点
    for (auto& i : tree[x])
    {
        //防止往上跑，如果遇到的节点是父节点，我们就不去
        if (i == y)continue;
        子节点的深度是父节点+1
        deep[i] = deep[x] + 1;
        dfs(i, x);
    }
}
​
//求x和y的最近公共祖先
int lca(int x, int y)
{
    //如果两节点深度不一样，我们把他们移动到同一深度
    if (deep[x] != deep[y])
    {
        //为了不麻烦，我们都只处理x
        //我们移动深度大的到上面
        if (deep[x] < deep[y])swap(x, y);
        for (int i = 20; i >= 0; i--)
        {
            //如果跳的点深度仍是大于等于y的，我们才跳（擦边球操作）
            if (deep[fa[x][i]] >= deep[y])
                x = fa[x][i];
        }
    }
    //如果深度一样了，俩节点相同，说明这个节点就是原来x和y的最近公共祖先
    if (x == y)return x;
    //开始俩边点一起往上跳
    for (int i = 20; i >= 0; i--)
    {
        //获取他俩的第2^i个祖先
        int a = fa[x][i], b = fa[y][i];
        //只有不一样了，我们才跳（擦边球操作）
        if (a != b)
        {
            x = a, y = b;
        }
    }
    //最后，它们的父节点就是最近公共祖先
    return fa[x][0];
}
​
void solve()
{
    int n, m, x, y;
    cin >> n >> m;
    for (int i = 1; i < n; i++)
    {
        cin >> x >> y;
        tree[y].push_back(x);
        tree[x].push_back(y);
    }
    //初始根节点深度设为1
    //注意是根节点，如果题目没说出，我们默认是1，如果说了，就按照题目说的来
    deep[1] = 1;
    dfs(1, 0);
    
    while (m--)
    {
        cin >> x >> y;
        cout << lca(x, y) << endl;
    }
}
​
signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t = 1;
    // cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

五、给我题！我要试一试！

P3379 【模板】最近公共祖先（LCA）

这题就是一个模板题，唯一要注意的是这题的根节点root是给定的，我们要按照给定的根节点来运算。

AC代码

#include<iostream>
using namespace std;
#include<vector>
#include<algorithm>
#include<math.h>
#include<set>
#include <random>
#include<numeric>
#include<string>
#include<string.h>
#include<iterator>
#include<fstream>
#include<map>
#include<unordered_map>
#include<stack>
#include<list>
#include<queue>
#include<iomanip>
#include<bitset>
​
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
​
#define endl '\n'
#define int ll
#define PI acos(-1)
#define INF 0x3f3f3f3f
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll, ll>PII;
const int N = 5e5 + 50, MOD = 998244353;
​
vector<int>tree[N];
int deep[N], fa[N][32];
​
int lca(int x, int y)
{
    if (deep[x] != deep[y])
    {
        if (deep[x] < deep[y])swap(x, y);
        for (int i = 20; i >= 0; i--)
        {
            if (deep[fa[x][i]] >= deep[y])x = fa[x][i];
        }
    }
    if (x == y)return x;
    for (int i = 20; i >= 0; i--)
    {
        int a = fa[x][i], b = fa[y][i];
        if (a != b)
        {
            x = a, y = b;
        }
    }
    return fa[x][0];
}
​
void dfs(int x, int y)
{
    fa[x][0] = y;
    for (int i = 1; i < 20; i++)
    {
        fa[x][i] = fa[fa[x][i - 1]][i - 1];
    }
    for (auto& i : tree[x])
    {
        if (i == y)continue;
        deep[i] = deep[x] + 1;
        dfs(i, x);
    }
    
}
​
void solve()
{
    int n, m, root, x, y;
    cin >> n >> m >> root;
    for (int i = 1; i < n; i++)
    {
        cin >> x >> y;
        tree[y].push_back(x);
​
        tree[x].push_back(y);
    }
    //按照题目给的根节点来运算
    deep[root] = 1;
    dfs(root, 0);
    
    while (m--)
    {
        cin >> x >> y;
        cout << lca(x, y) << endl;
    }
}
​
signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t = 1;
    // cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

Problem - 2586 (hdu.edu.cn)

这题是让我们求树中任意两个点之间的距离。

其实这就是lca非常常见的用法了，比如这么一棵树：

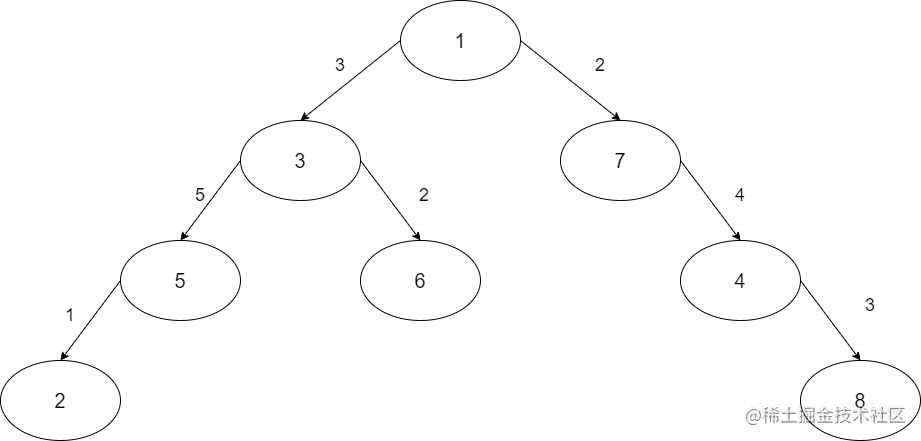
未命名绘图14.png

我们先求出所有点到达根节点的距离，这步只需要在dfs和深度一起处理。

用一个数组dis记录下来，dis[i]表示节点i到根节点的距离为dis[i]:

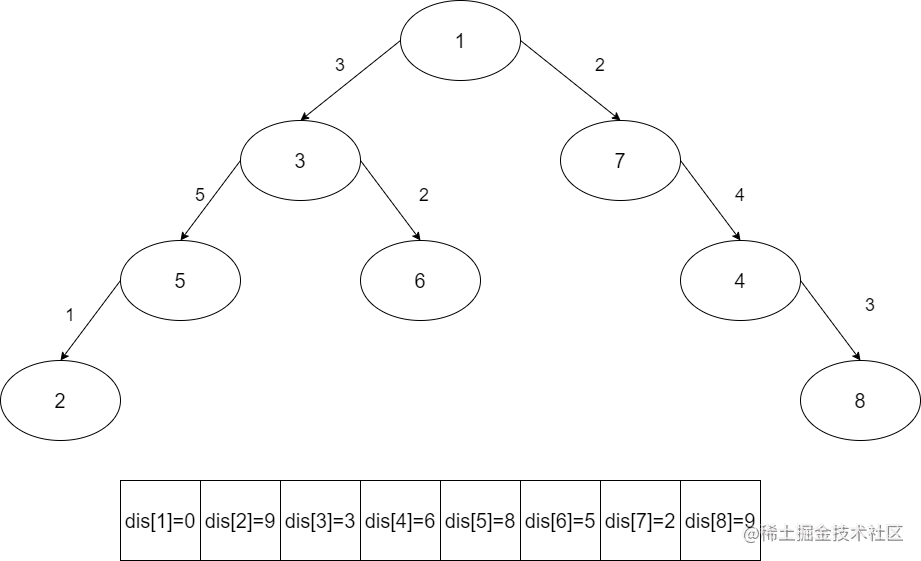
未命名绘图15.png

如果我们想求点x到点y的距离，只需要求得他俩的最近公共祖先z，此时x和y的距离是：

l e n = d i s [ x ] + d i s [ y ] − 2 ∗ d i s [ z ] ; len=dis[x]+dis[y]-2*dis[z]; len=dis[x]+dis[y]−2∗dis[z];

比如我们想求2和6的距离，可以发现转折点在3，也就是他俩的公共祖先。

  1. 那么点2到点3的距离就为：dis[2]-dis[3]；
  2. 再求点6到点3的距离就为：dis[6]-dis[3]；
  3. 那么点2的距离到点6的距离就为：dis[2]+dis[6]-dis[3]-dis[3];

只要我们知道这两点的最近公共祖先，我们就可以很快的求出这两点的距离了。

AC代码

#include<iostream>
using namespace std;
#include<vector>
#include<algorithm>
#include<math.h>
#include<set>
#include <random>
#include<numeric>
#include<string>
#include<string.h>
#include<iterator>
#include<fstream>
#include<map>
#include<unordered_map>
#include<stack>
#include<list>
#include<queue>
#include<iomanip>
#include<bitset>
​
//#pragma GCC optimize(2)
//#pragma GCC optimize(3)
​
#define endl '\n'
#define int ll
#define PI acos(-1)
#define INF 0x3f3f3f3f
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll, ll>PII;
const int N = 5e5 + 50, MOD = 998244353;
​
vector<int>tree[N];
int deep[N], fa[N][32], dis[N];
//存储的是边权
unordered_map<int, unordered_map<int, int>>mymap;
​
int lca(int x, int y)
{
    if (deep[x] != deep[y])
    {
        if (deep[x] < deep[y])swap(x, y);
        for (int i = 20; i >= 0; i--)
        {
            if (deep[fa[x][i]] >= deep[y])x = fa[x][i];
        }
    }
    if (x == y)return x;
    for (int i = 20; i >= 0; i--)
    {
        int a = fa[x][i], b = fa[y][i];
        if (a != b)
        {
            x = a, y = b;
        }
    }
    return fa[x][0];
}
​
void dfs(int x, int y)
{
    fa[x][0] = y;
    for (int i = 1; i < 20; i++)
    {
        fa[x][i] = fa[fa[x][i - 1]][i - 1];
    }
    for (auto& i : tree[x])
    {
        if (i == y)continue;
        deep[i] = deep[x] + 1;
        //i点到1的距离就是：父节点到1的距离+父节点到它的距离
        dis[i] = dis[x] + mymap[x][i];
        dfs(i, x);
    }
    
}
​
void solve()
{
    //因为是多组数据，所以每次要把stl清空
    tree->clear();
    mymap.clear();
    int n, m, x, y, w;
    cin >> n >> m;
    for (int i = 1; i < n; i++)
    {
        cin >> x >> y >> w;
        tree[y].push_back(x);
        tree[x].push_back(y);
        mymap[x][y] = w;
        mymap[y][x] = w;
    }
    //题目没给我们root，我们设1为根
    deep[1] = 1;
    dfs(1, 0);
    
    while (m--)
    {
        cin >> x >> y;
        int z = lca(x, y);
        cout << dis[x] + dis[y] - dis[z] * 2 << endl;
    }
}
​
signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t = 1;
     cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

六、完结

看到这里恭喜你又学会了一个新的知识点，鼓掌（啪啪啪啪）

不过我想说的是，学习一个新的知识点不难，难的是如何玩出花来。

光看文章或视频肯定是不够的，这些只是帮你入门的媒介，更重要的是你后续的努力，只有多些题积累经验，才能更好的掌握知识点。

千言万语汇成一句话——多刷题！

最后如果本篇文章帮到了您，不知是否能点一个小小的赞呢。（拜托了！这对我真的很重要！）

​

QQ图片20230402115236.gif

​

那么我们在下一个知识点再见啦！拜拜！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/424107.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

5.redis-哨兵模式

5.redis-哨兵模式

01-哨兵模式概述 如果master宕机, 我们该怎么办? ①关闭所有slave②选举新的master, 建立新的主从结构 存在的问题 ①关闭期间, 谁来提供数据服务②选举新master的标准是什么③原来的master恢复了怎么办 哨兵模式 sentinel是一个分布式系统&#xff0c;用于对主从结构中的每…
阅读更多...
【多线程】Thread类

【多线程】Thread类

1. Java中如何进行多线程编程&#xff1f;线程是操作系统中的概念&#xff0c;操作系统内核实现了线程这样的机制&#xff0c;并且对用户层提供了一些 API 供用户使用(如 Linux 中的 pthread 库)。所以本身关于线程的操作&#xff0c;是依赖操作系统提供的的 API&#xff0c;而…
阅读更多...
练习，异常，异常处理，try-catch,throws

练习，异常，异常处理，try-catch,throws

package com.jshedu.homework_;/*** author Mr.jia* version 1.0*/ //匿名内部类 public class Homework04 {public static void main(String[] args) {Cellphone cellphone new Cellphone();//1.匿名内部类&#xff0c;同时也是一个对象/*new computer() {Overridepublic dou…
阅读更多...
JavaClient With HDFS

JavaClient With HDFS

序言 在使用Java创建连接HDFS的客户端时,可以设置很多参数,具体有哪些参数呢,只要是在部署HDFS服务中可以设置的参数,都是可以在连接的时候设置. 我没有去验证所有的配置是否都可以验证,只是推测cuiyaonan2000163.com 依据 创建HDFS的构造函数如下所示: 网上比较常用的是get…
阅读更多...
gdb 跟踪调式core

gdb 跟踪调式core

自己编译的问题出现段错误： 编译：使用gdb调试core文件来查找程序中出现段错误的位置时，要注意的是可执行程序在编译的时候需要加上-g编译命令选项。 gdb调试core文件的步骤 gdb调试core文件的步骤常见的有如下几种，推荐第一种。 具体步骤一： （1）启动gdb，进入core文…
阅读更多...
【剑指 offer】旋转数组的最小数字

【剑指 offer】旋转数组的最小数字

✨个人主页&#xff1a;bit me&#x1f447; ✨当前专栏&#xff1a;算法训练营&#x1f447; 旋 转 数 组 的 最 小 数 字核心考点&#xff1a;数组理解&#xff0c;二分查找&#xff0c;临界条件 描述&#xff1a; 有一个长度为 n 的非降序数组&#xff0c;比如[1,2,3,4,5]…
阅读更多...
ABAP 创建、修改、删除内部交货单（VL31N/VL32N）

ABAP 创建、修改、删除内部交货单（VL31N/VL32N）

一、干货 VL31N创建的BAPI&#xff1a; 1.GN_DELIVERY_CREATE 通用交货单使用的bapi&#xff0c;推荐使用 2.BAPI_DELIVERYPROCESSING_EXEC 简单&#xff0c;但是字段比较少 3.BBP_INB_DELIVERY_CREATE 听说有bug&#xff0c;我就没有使用这个了 VL32N修改/删除BAPI: BAPI_INB…
阅读更多...
每日学术速递4.14

每日学术速递4.14

CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CV 1.Deep RL at Scale: Sorting Waste in Office Buildings with a Fleet of Mobile Manipulators 标题&#xff1a;大规模深度强化学习&#xff1a;使用移动机械手对办公楼中的垃圾进行…
阅读更多...
VS2022编译libui库

VS2022编译libui库

libui是一个 C 中简单且可移植（但并非不灵活）的 GUI 库，它使用每个平台原生的GUI技术进行绘制。 官网地址：链接 本文将使用VS2022编译libui库，操作系统为Windows10。 1. 下载源代码 首先在官网下载源代码，由于此代码不依赖第三库，故只需下载源代码即可进行编译。 我下…
阅读更多...
R730服务器环境搭建（centos7、lanproxy、docker、k8s）

R730服务器环境搭建（centos7、lanproxy、docker、k8s）

文章目录前言一、centos7安装1.制作u盘启动盘2.开始装系统&#xff1a;二、环境安装&#xff08;lanproxy、docker、k8s&#xff09;1.lanproxy安装2.docker安装&#xff08;如果通过k8sOfflineSetup安装k8s可以跳过这一步&#xff0c;因为会自动安装docker&#xff09;3.安装k…
阅读更多...
安装 KeyShot 流程

安装 KeyShot 流程

| 安装 KeyShot 流程 KeyShot 安装程序将指导您完成安装过程。 在 Windows 上&#xff0c;安装过程会要求您考虑以下事项终用户协议 为使用计算机的所有人或仅为当前用户安装 KeyShot 安装文件夹的位置 资源文件夹的位置 ——资源文件夹包含许多可以与 KeyShot 一起使用的纹…
阅读更多...
NSSCTF doublegame题解

NSSCTF doublegame题解

运行一下&#xff0c;是一个贪吃蛇游戏 先玩一玩&#xff0c;蛇的移动速度太快了&#xff0c;玩不了 查壳 64位文件&#xff0c;无壳 进入IDA分析 发现这个EXE文件是开了程序基址随机化&#xff0c;就是每次用IDA打开指令的地址不一样 我们要想使用x64dbg和IDA的时候&#…
阅读更多...
Docker的基本操作

Docker的基本操作

文章目录一、 Docker的基本操作1.1 镜像1.1.1 介绍1.1.2 镜像操作1.2 容器1.2.1 介绍1.2.2 容器操作1.3 数据卷1.3 介绍1.3.2 数据卷操作一、 Docker的基本操作 1.1 镜像 1.1.1 介绍 在 Docker 中&#xff0c;镜像&#xff08;Image&#xff09;是一种轻量级、可移植的、可扩…
阅读更多...
营销平台一站式集成 高效实现自动化

营销平台一站式集成 高效实现自动化

市面上广告投放渠道渠道那么多&#xff0c;图文、动图、短视频等广告形式也越来越多&#xff0c;许多企业都会有这些疑问&#xff1a; 「腾讯广告、百度营销、巨量引擎哪个广告渠道的客户适合我们公司&#xff1f;」 「这么多广告渠道&#xff0c;哪家的点击率、转化率比较高…
阅读更多...
1.Antlr4-简介入门

1.Antlr4-简介入门

1.简介: ANTLR v4是一款功能强大的语法分析器生成器&#xff0c;可以用来读取、处理、执行和转换结构化文本或二进制文件。它被广泛应用于学术界和工业界构建各种语言、工具和框架。 2 关键字&#xff1a; import, fragment, lexer, parser, grammar, returns, locals, throw…
阅读更多...
运维——记一次接口超时的问题与解决方法(HttpException: Read timed out)

运维——记一次接口超时的问题与解决方法(HttpException: Read timed out)

前言&#xff1a;近期,一个线上的项目,请求出现了大量接口超时的问题,找了几个小时原因,最终发现是因为数据库服务器的磁盘满了,在此记录一下寻找的过程以及发现的问题,以备后续参考。 环境&#xff1a; 项目服务器(CentOS 64-bit 7.9) OpenJDK 1.8.0_272 数据库服务器(CentO…
阅读更多...
打怪升级之FPGA组成原理（LE部分）

打怪升级之FPGA组成原理（LE部分）

FPGA芯片逻辑单元的原理 不论你使用哪一款FPGA芯片&#xff0c;其核心可编程逻辑单元都是从一段内存种按顺序读取执行并执行的过程。具体来说&#xff0c;FOGA芯片内部包括可编程逻辑块(LAB)、可配置输入输出单元(IOE)、时钟管理模块、嵌入式RAM(BRAN&#xff0c;在Cyclone IV…
阅读更多...
【堆的使用】【dfs构建数】二叉树遍历

【堆的使用】【dfs构建数】二叉树遍历

二叉树遍历方法一&#xff1a;方法二&#xff1a;利用堆的性质原题链接 方法一&#xff1a; 利用dfs构建树 因为这个前序遍历给了我们空的叶节点 所以我们可以只根据叶节点 构建树 abc##de#g##f### 构建图如下 我们根据前序 abc##de#g##f### 发现 dfs左子树 和 右子树 当…
阅读更多...
mac系统下使用clion调试redis源码

mac系统下使用clion调试redis源码

获取源代码 有两种方式&#xff0c;第一种是从官网下载 Redis 源码压缩包&#xff0c;如图 1-1 所示。 图1-1 将压缩包解压得到一个文件夹。 第二种方式&#xff0c;通过 git clone 获取源码。 从 Github 上&#xff0c;使用 git clone https://github.com/redis/redis.git…
阅读更多...
第1章-JVM与Java体系结构

第1章-JVM与Java体系结构

1、本系列博客&#xff0c;主要是面向Java8的虚拟机。如有特殊说明&#xff0c;会进行标注。 2、本系列博客主要参考尚硅谷的JVM视频教程&#xff0c;整理不易&#xff0c;所以图片打上了一些水印&#xff0c;还请读者见谅。后续可能会加上一些补充的东西。 3、尚硅谷的有些视频…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023