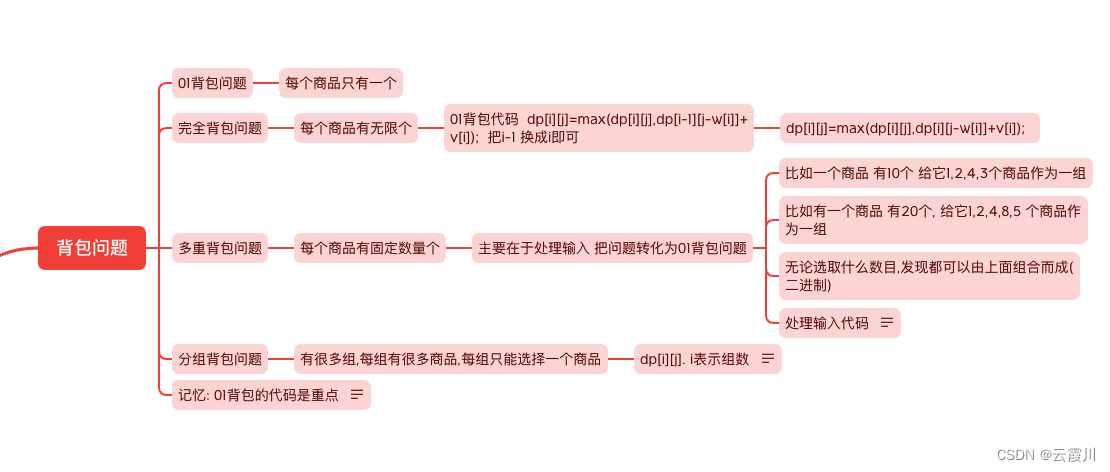
背包问题
容量有限的背包,给很多商品,商品有相应的体积与价值
01背包问题
一个背包 每个物品只有一个

最终状态方程
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])
推导过程
由上一层推导过来
选择拿不拿i
最终代码
#include<iostream>
#include<vector>
using namespace std;
// 1 2 3 4 5 分别代表商品编号
int bag_01(int n,int b,vector<int> &v,vector<int> &w)
{
// b 代表bag v代表价值 w代表weight
vector<vector<int>> dp(n+1,vector<int>(b+1));
//int dp[v.size()+1][b+1]; // 代表选完i产品,背包有b容积 能获得的最大价值
// 当i=0时
for(int i=1;i<=n;i++)
{
for(int j=0;j<=b;j++)
{
// 等于在背包容积允许的情况下给背包加了重量,同时也加入了价值
dp[i][j]=dp[i-1][j];
if(j>=w[i]) dp[i][j]=max(dp[i][j],dp[i-1][j-w[i]]+v[i]);
}
}
return dp[n][b];
}
int main()
{
// dp[i][j] i 表示第i次选择 j表示剩余的体积
int n=0;
cin>>n;
vector<int> v(n+1);
vector<int> w(n+1);
int b=0;
cin>>b;
for(int i=1;i<=n;i++)
{
cin>>w[i]>>v[i];
}
cout<<bag_01(n,b,v,w)<<endl;
}
完全背包问题
每个商品无限个

最终状态方程
dp[i][j]=max(dp[i-1][j],dp[i][j-w[i]]+v[i])
推导过程
每个物品无限个,尝试为每个产品都尝试塞进去
for(int i=1;i<=n;i++)
{
for(int j=0;j<=b;j++)
{
for(int k=0;j*w[i]<=j;k++)
{
dp[i][j]=max(dp[i][j],dp[i-1][j-k*w[i]]+k*v[i]);
}
}
}
可以转化为2维,[i][j]中与[i][j-w[i]] 有很相似的部分
[i][j]=max([i-1][j],[i-1][j-w]+v,[i-1][j-2w]+2v,[i-1][j-3w]+3v....)
[i][j-w]=max([i-1][j-w],[i-1][j-2w]+v,[i-1][j-3w]+2v....).
[i][j]=max([i-1][j],[i][j-w]+v)
最终代码
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int whole_bag(int n,int b,vector<int> &v,vector<int> &w)
{
//cout<<"进入"<<endl;
vector<vector<int> > dp(n+1,vector<int>(b+1));
for(int i=1;i<=n;i++)
{
for(int j=0;j<=b;j++)
{
dp[i][j]=dp[i-1][j];
if(j>=w[i])
{
dp[i][j]=max(dp[i][j],dp[i][j-w[i]]+v[i]);
}
}
}
return dp[n][b];
}
int main()
{
int n=0;
cin>>n;
vector<int> v(n+1);
vector<int> w(n+1);
int b=0;
cin>>b;
for(int i=1;i<=n;i++)
{
cin>>w[i]>>v[i];
}
cout<<whole_bag(n,b,v,w)<<endl;
}
多重背包问题
每个物品数量不一样

推导过程
朴素解法,给k的数目加上一个限制
for(int i=1;i<=n;i++)
{
for(int j=0;j<=b;j++)
{
for(int k=0;k*w[i]<=j&&k<=s[i];k++)
{
dp[i][j]=max(dp[i][j],dp[i-1][j-k*w[i]]+k*v[i]);
}
}
}
看能否采用完全背包的优化方法呢?
[i][j]=max([i-1][j],[i-1][j-w]+v,[i-1][j-2w]+2v,[i-1][j-3w]+3v+...+[i-1][j-sw]+sw)
[i][j-w]=max([i-1][j-w],[i-1][j-2w]+v,[i-1][j-3w]+2v....+[i-1][j-sw]+(s-1)w+[i-1][j-(s+1)w]+sw).
会发现[i][j-w] 多了一项,这就无法用max
采用二进制方法优化,将 多重背包问题 转化成 01背包问题
如一个商品有100个
1 个 作为一个商品
2 个 作为一个商品
4 个 作为一个商品
8 个 作为一个商品
.. 最后一个商品用剩余的数目当成整体商品
512 个 作为一个商品
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int bag_01(int n,int b,vector<int>&w,vector<int>&v)
{
vector<vector<int> > dp(n+1,vector<int>(b+1));
for(int i=1;i<=n;i++)
{
for(int j=0;j<=b;j++)
{
dp[i][j]=dp[i-1][j];
if(j>=w[i]) dp[i][j]=max(dp[i][j],dp[i-1][j-w[i]]+v[i]);
}
}
return dp[n][b];
}
int main()
{
int n_fake=0;
cin>>n_fake;
int b=0;
cin>>b;
int n=0;
vector<int> v;
vector<int> w;
v.push_back(-1);
w.push_back(-1);
for(int i=1;i<=n_fake;i++)
{
int l1,l2,l3;
// l1 是 体积
// l2 是 价值
// l3 是 个数
cin>>l1>>l2>>l3;
int k=1;
while(k>=l3)
{
l3-=k;
v.push_back(l2*k);
w.push_back(l1*k);
n+=1;
k*=2;
}
if(l3!=0)
{
v.push_back(l2*k);
w.push_back(l1*k);
}
}
cout<<bag_01(n,b,w,v)<<endl;
}
分组背包问题

物品有n组,每组物品有若干个,每组最多选一个
分组背包问题
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i,k]]+v[i,k])
选择第k个商品
类似多重背包问题的朴素写法,非常符合逻辑
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int group_bag(int n,int b,vector<vector<int> >& w,vector<vector<int> >& v)
{
vector<vector<int> > dp(n+1, vector<int>(b+1));
for(int i=1;i<=n;i++)
{
for(int j=0;j<=b;j++)
{
dp[i][j]=dp[i][j-1];
for(int l=0;l<v[i].size();l++)
{
if(w[i][l]<=j) dp[i][j]=max(dp[i][j],dp[i-1][j-w[i][l]]+v[i][l]);
}
}
}
return dp[n][b];
}
int main()
{
vector<vector<int> > w;
vector<vector<int> > v;
int n=0;
int b=0;
cin>>n>>b;
w.push_back(vector<int>(1));
v.push_back(vector<int>(1));
for(int i=1;i<=n;i++)
{
int n1=0;
cin>>n1;
vector<int> v1(n1);
vector<int> w1(n1);
for(int j=0;j<n1;j++)
{
int a=0;
int b=0;
cin>>a>>b;
w1.push_back(a);
v1.push_back(b);
}
w.push_back(w1);
v.push_back(v1);
}
cout<<group_bag(n,b,w,v)<<endl;
}
欢迎大家 star ✨ GitHub - stolendance/acwing
正在更新算法模板 写上去就能用