第一章DFA
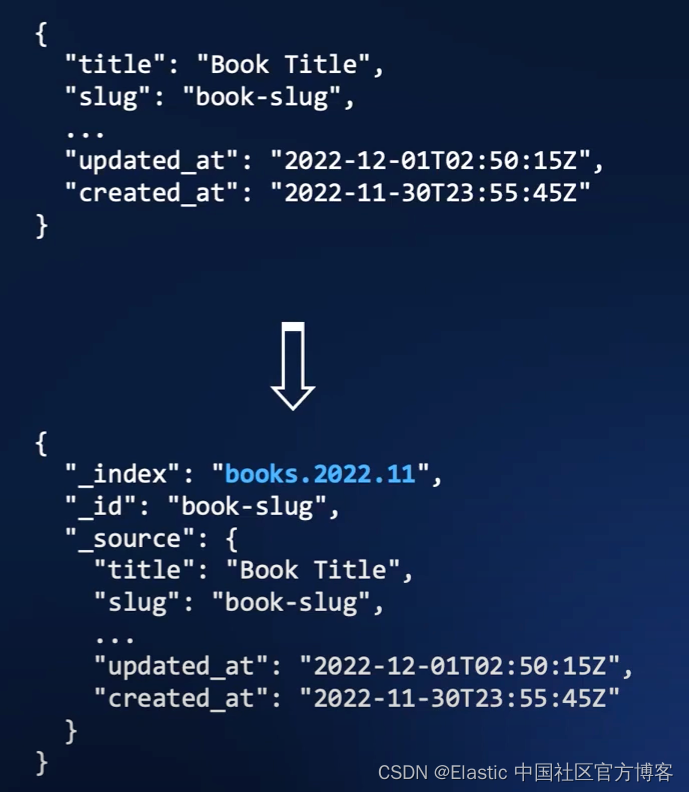
形式定义和状态转移函数:
DFA是一种特殊的NFA,
A={Q,,
,
,F} Q:输入状态集,∑:字母表,δ:状态转移函数Q×∑→Q q0∈Q初始状态 F终结集
设计举例
1.设计接受偶数个0和偶数个1串的DFA
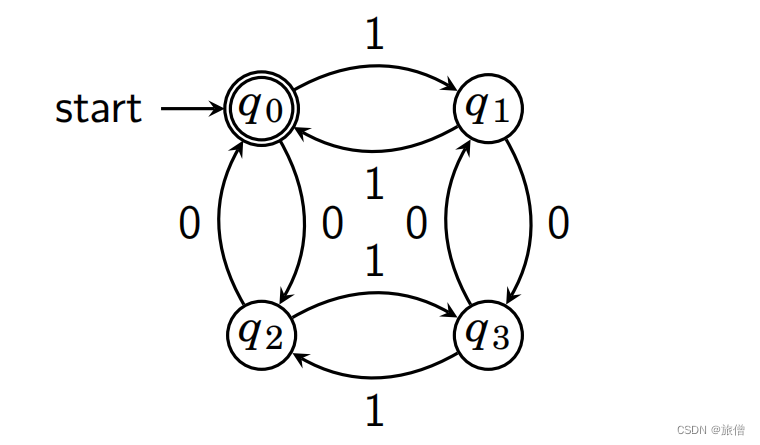
2.设计 DFA 接受 {0,1} 上的字符串 w, 且 w 是 3 的倍数的二进制表示(前面可以有0)
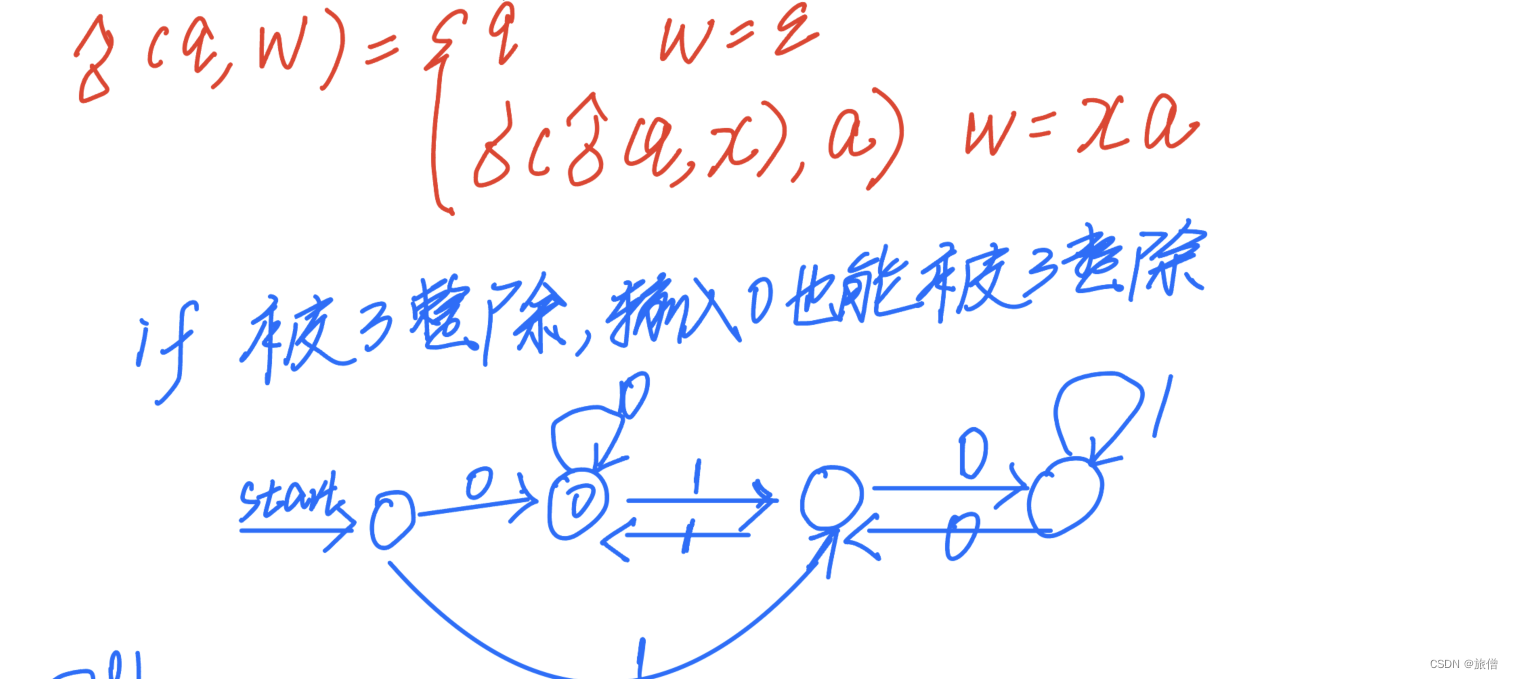
3.要求同上,前面不允许有0
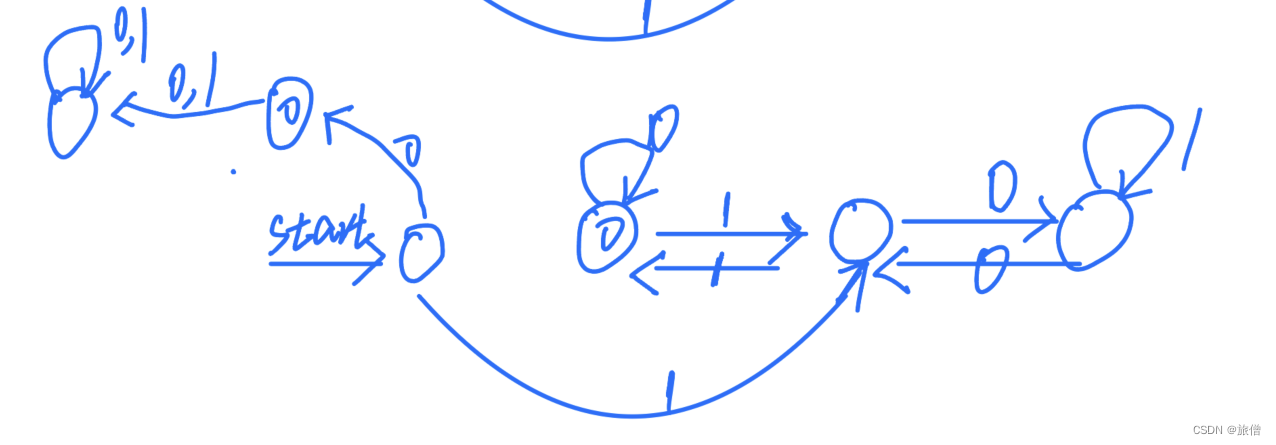
扔出来一个死状态。
4.Design a DFA for L = {w ∈ {0,1} ∗ | w contains both 00 and 11 as substrings}.(最后一个状态没加入01)
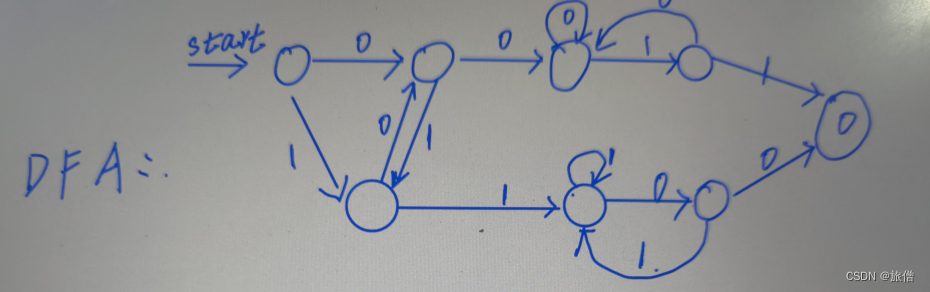
5.

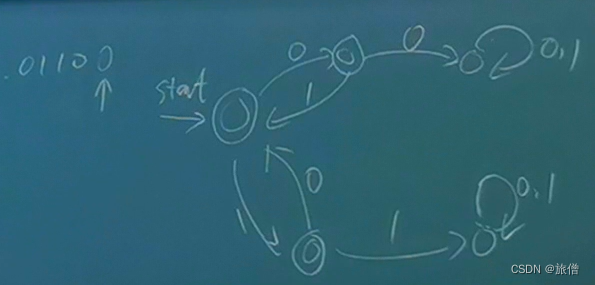
第2章NFA
NFA的设计
NFA的习题很少可以尝试将DFA的题变成NFA的题。
1.设计一个由01构成的串,1是偶数0是奇数的NFA
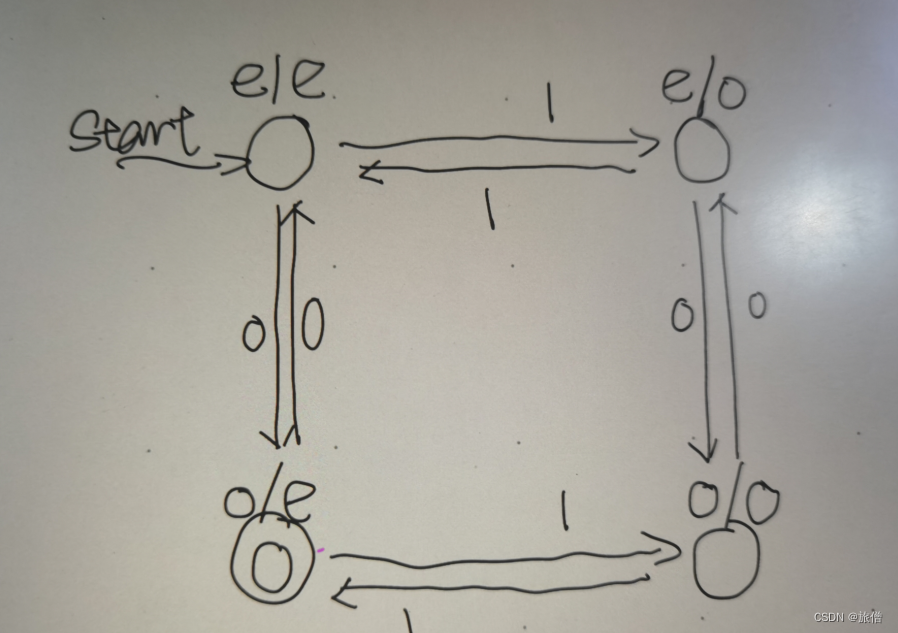
对0 1的状态进行区分
2. Design an NFA within four states for the language { 0 }* { 01 }*.
3.Design an NFA for L = { w∈{0,1}∗ | w contains an equal number of occurrences of the substrings 01 and 10 }
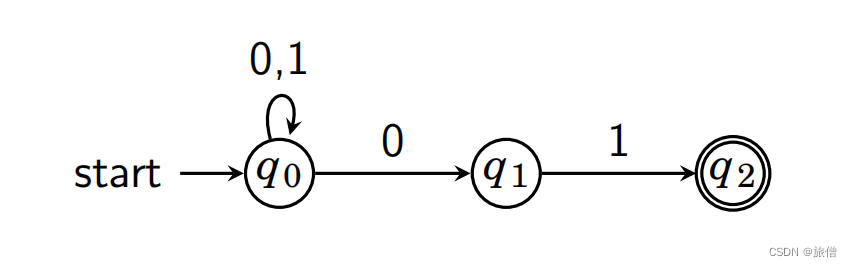
4.由 0 和 1 构成的串中, 接受全部以 01 结尾的串
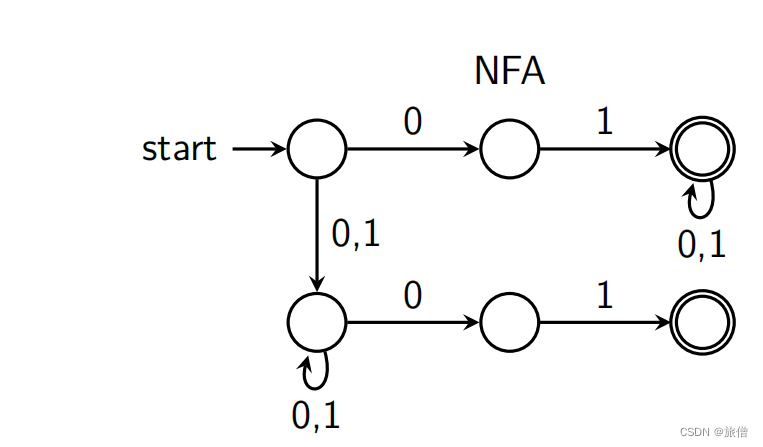
5.. 设计 L = {w ∈ {0,1}w的首尾字符相同}的 NFA 很容易忘了中间的情况
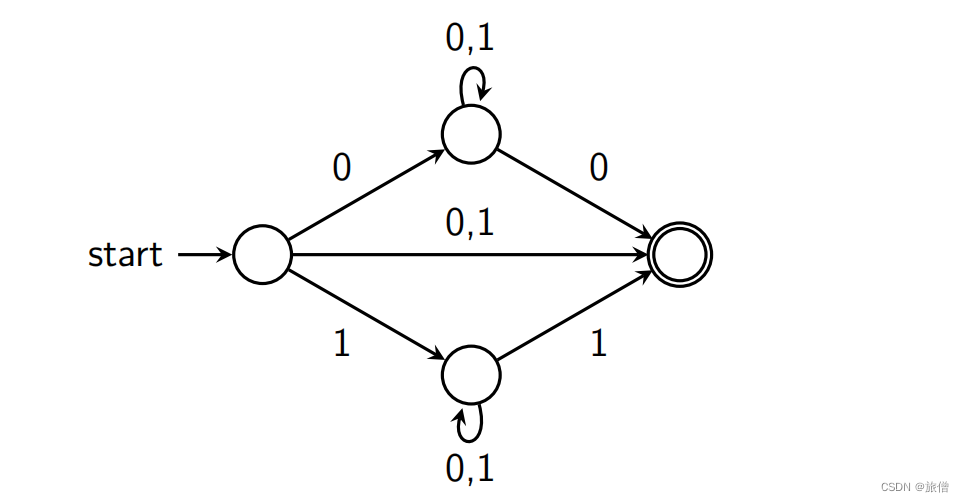
6.L = {w ∈ {0,1} *|w either begins or ends (or both) with 01. }
7.对以下几种语言设计NFA :

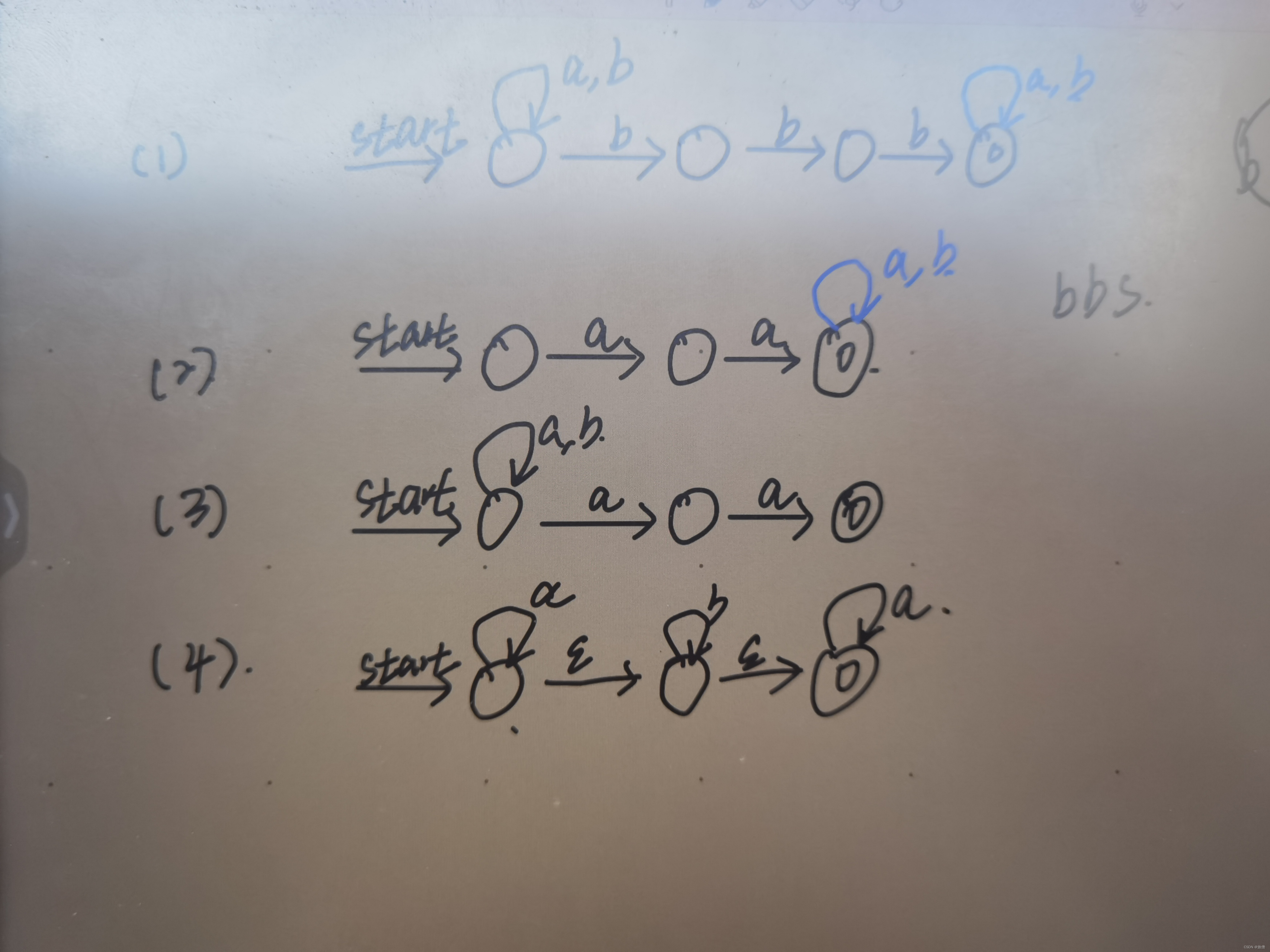
8.Design a NFA for L = {w ∈ {0,1} ∗ | w contains both 00 and 11 as substrings}.
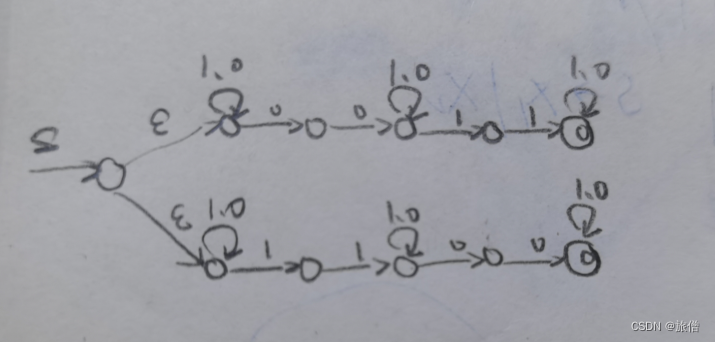
9.Design an NFA for L = {w ∈ {0,1} ∗ | w contains an equal number of occurrences of the substrings 01 and 10}.
做这种题的时候观察他的结构,猜想这种结构有什么特点.永远不要忘了中间的情况。
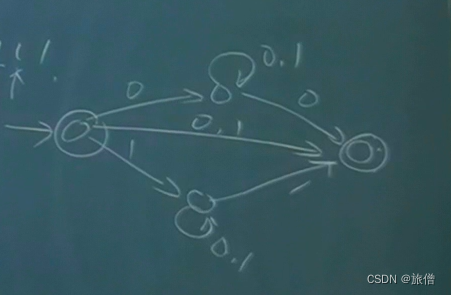
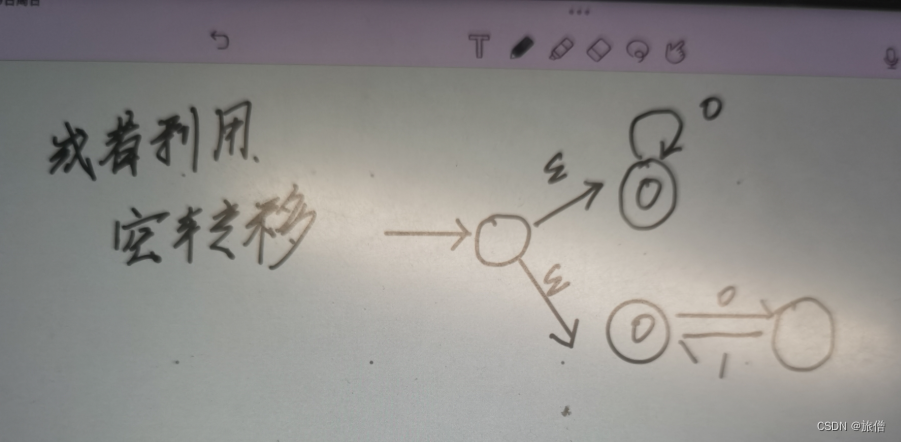
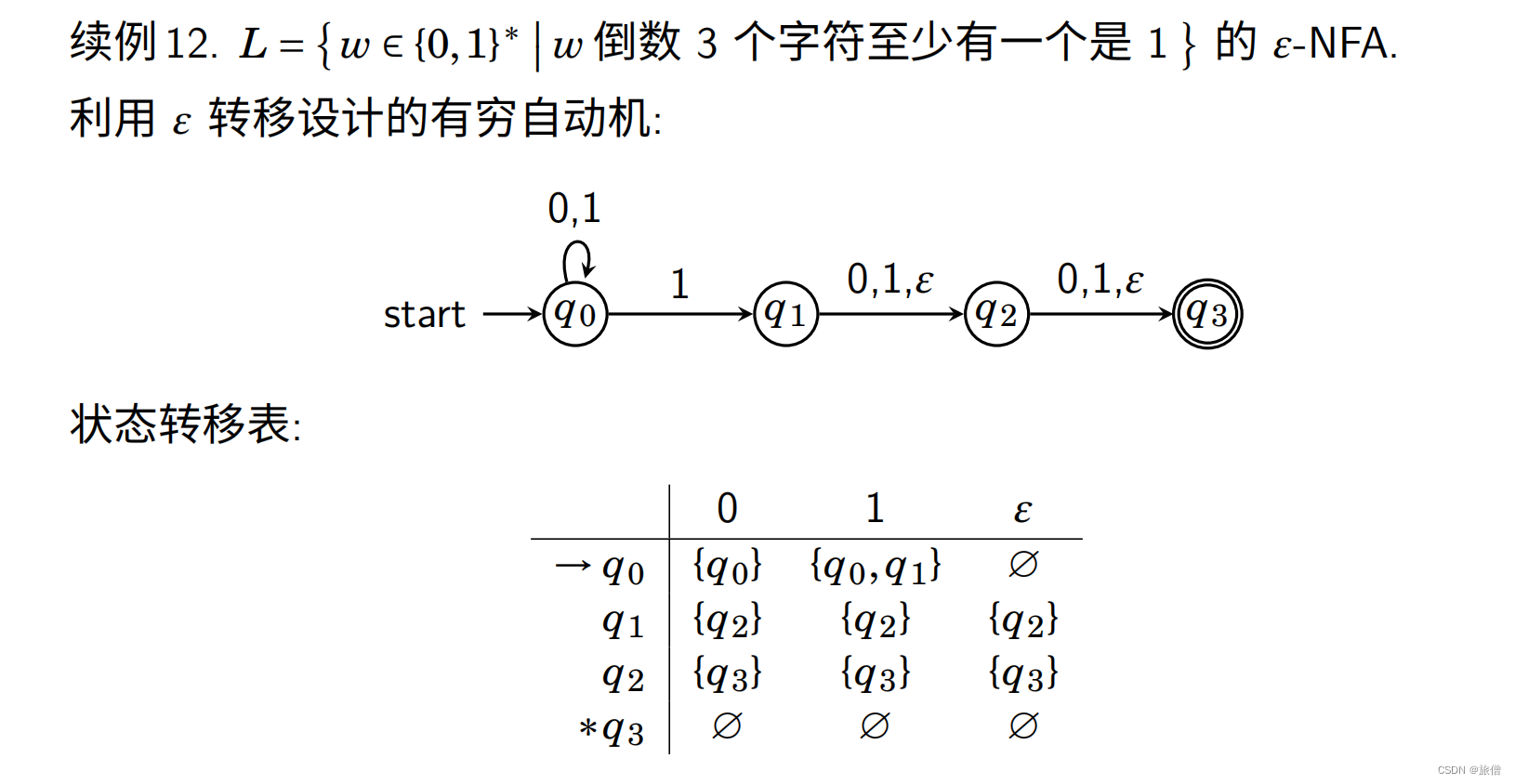
ε-NFA:
空转移有利于减少我们的状态并且自然的将条件分隔开来。
DFA和NFA的相互转换
等价性证明
NFA->DFA 理解思想吧。
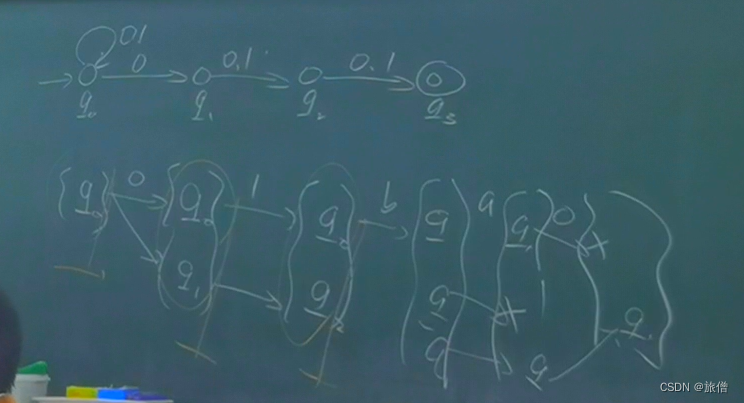


NFA转DFA 子集构造法:
注意一点:对于与其他子集一样用到就保留,没用到就去掉,NFA卡死,对应到DFA就是死状态
1.

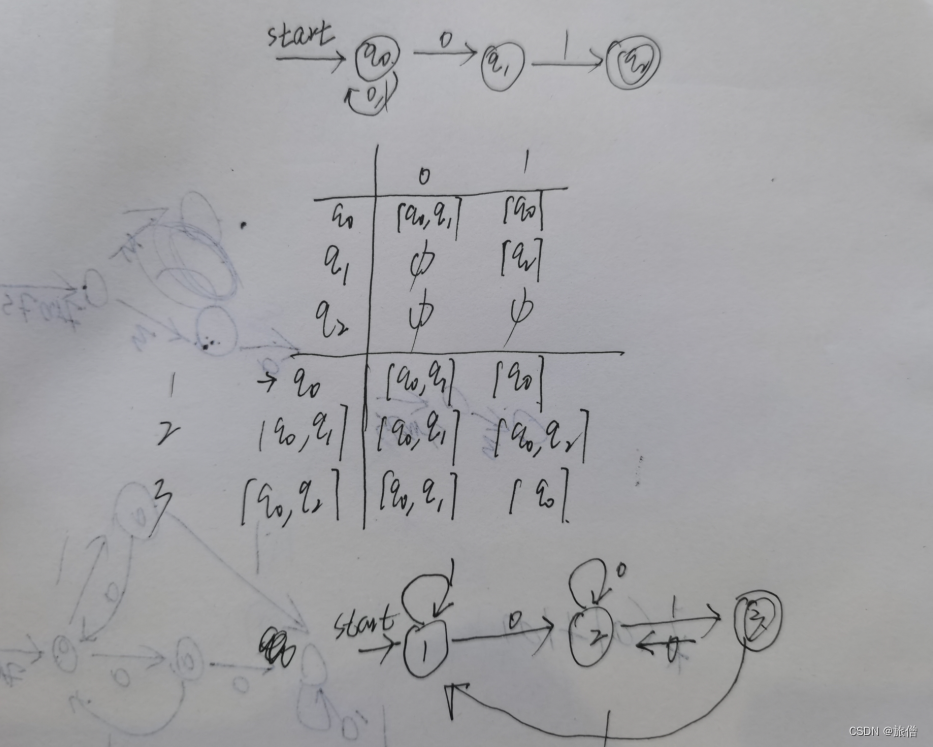
2.L = {(0+1)*|倒数第三个字符是1}的NFA转换成DFA
3.
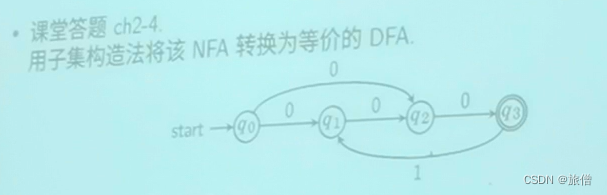
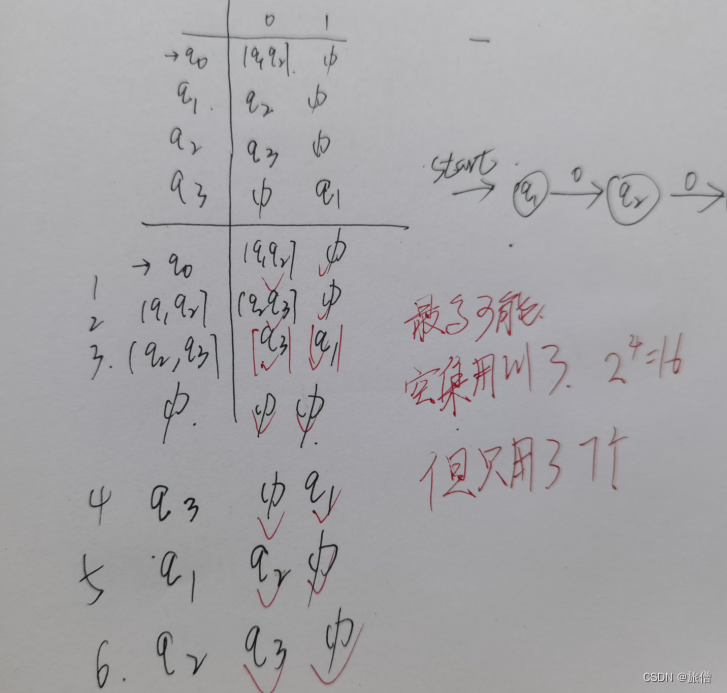
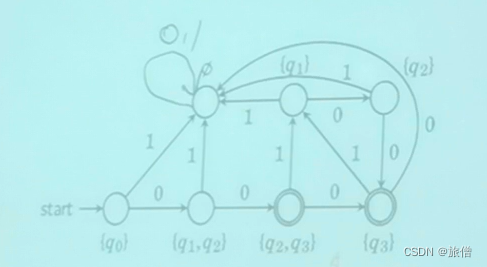
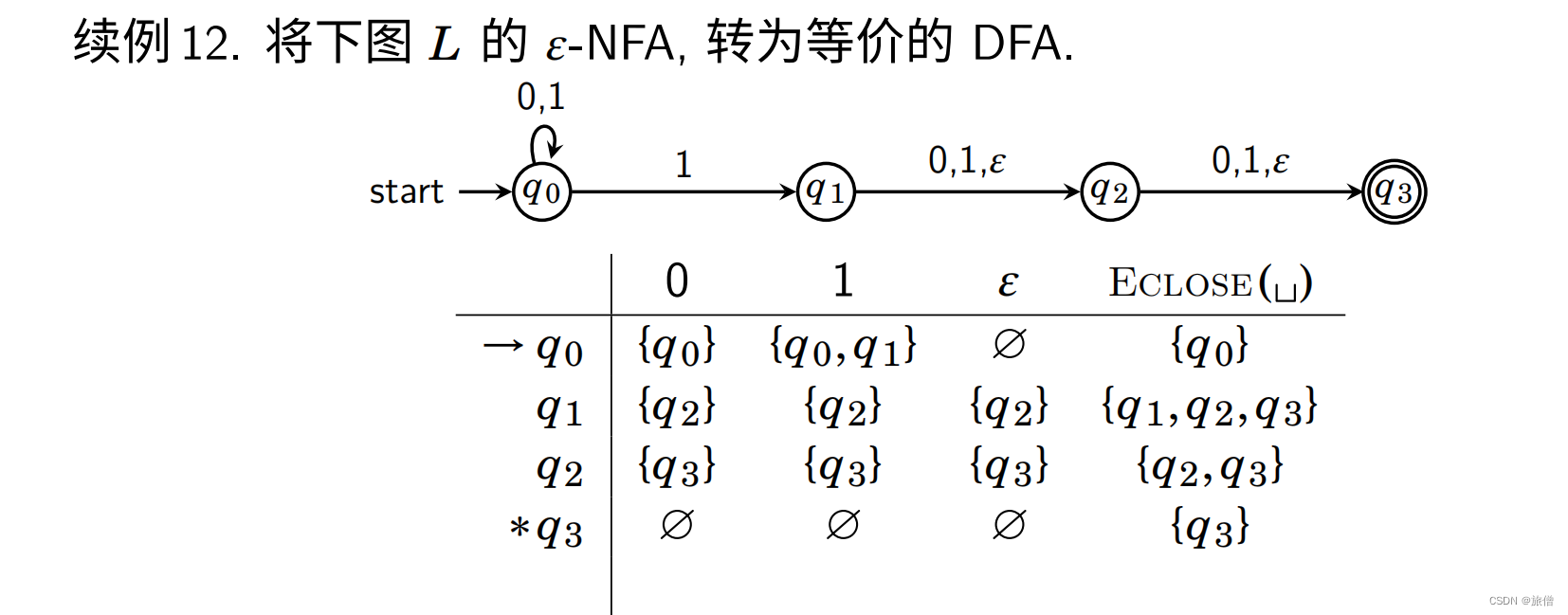
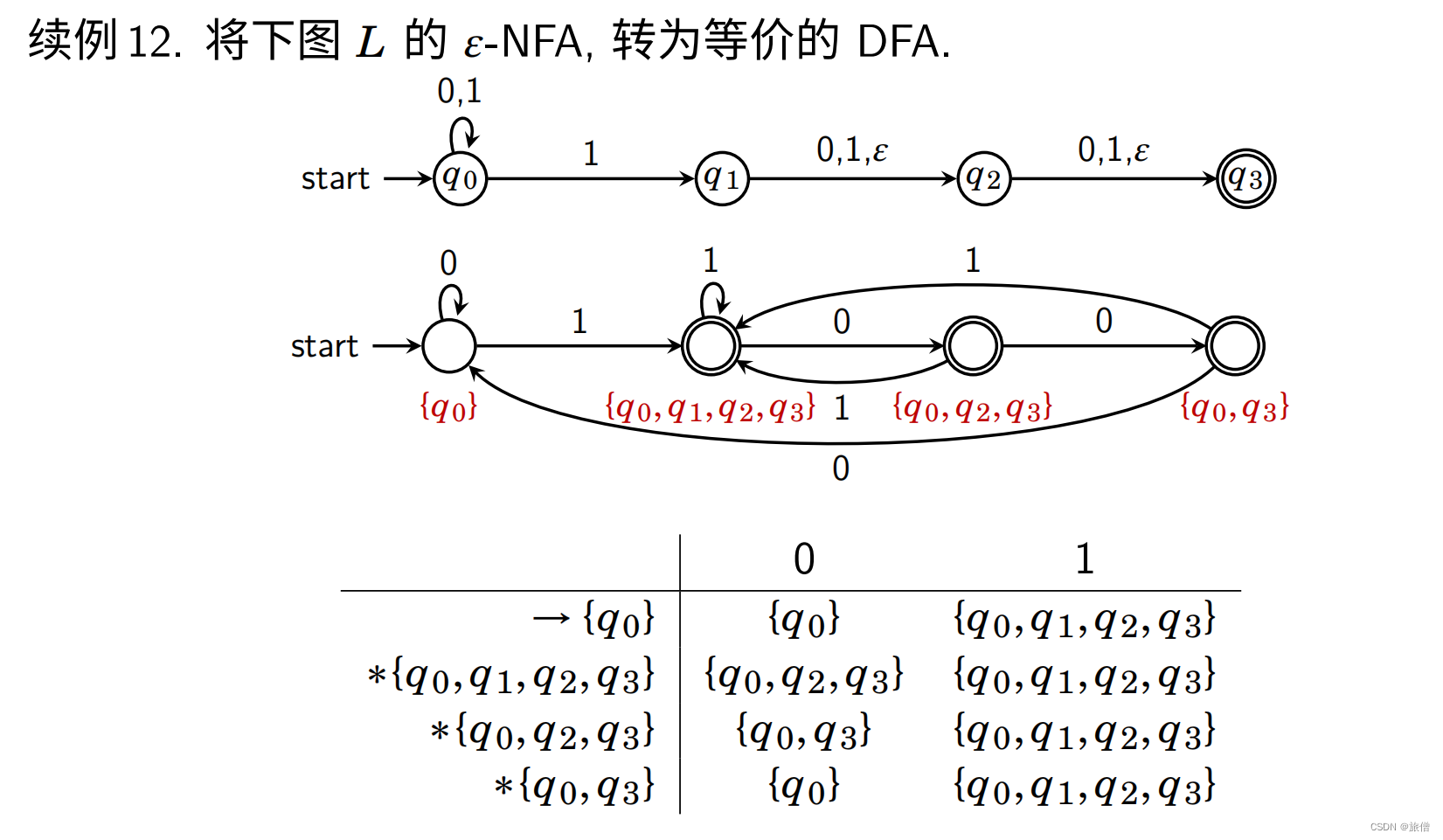
ε-NFA转换为DFA