五、回顾查找问题(参见练习 2.1-3)，注意到，如果序列 A 已排好序，就可以将该序列的中点与v进行比较。根据比较的结果，原序列中有一半就可以不用再做进一步的考虑了。二分查找算法重复这个过程，每次都将序列剩余部分的规模减半。为二分查找写出迭代或递归的伪代码。证明:二分查找的最坏情况运行时间为 O(lgn)。

文心一言：

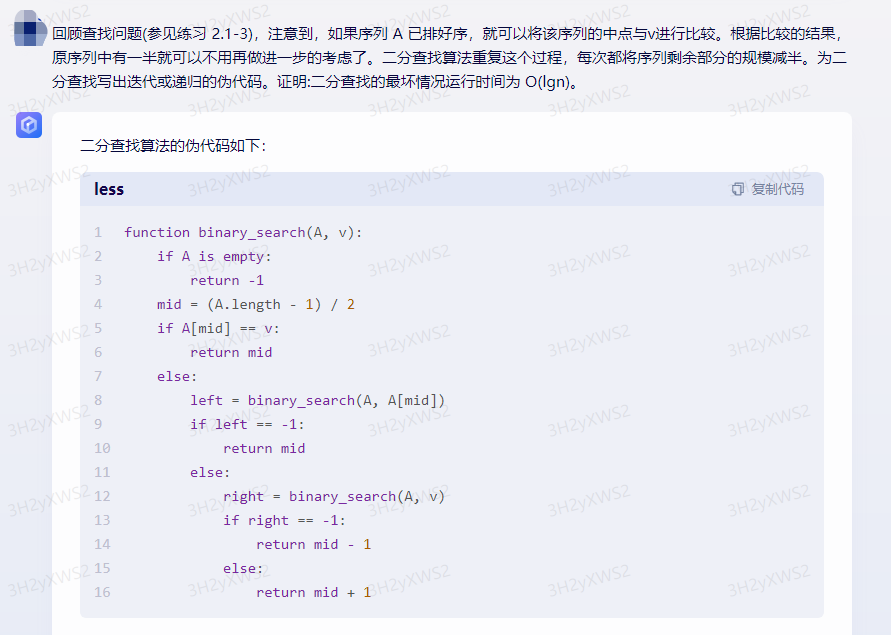
二分查找算法的伪代码如下：

function binary_search(A, v):  
    if A is empty:  
        return -1  
    mid = (A.length - 1) / 2  
    if A[mid] == v:  
        return mid  
    else:  
        left = binary_search(A, A[mid])  
        if left == -1:  
            return mid  
        else:  
            right = binary_search(A, v)  
            if right == -1:  
                return mid - 1  
            else:  
                return mid + 1

其中，A 是待查找的有序序列，v 是要查找的元素。在每次迭代中，我们首先检查序列的中点是否等于要查找的元素，如果是，则返回中点的下标。否则，我们将序列剩余部分的规模减半，并递归地查找左半部分和右半部分。如果左半部分的下标小于要查找的元素的下标，则返回左半部分的下标；否则，返回右半部分的下标。

证明：

二分查找的最坏情况运行时间为 O(lgn)。

证明：

二分查找的最坏情况运行时间为 O(lgn)。

证明：

二分查找的最坏情况运行时间为 O(lgn)。

chatgpt：

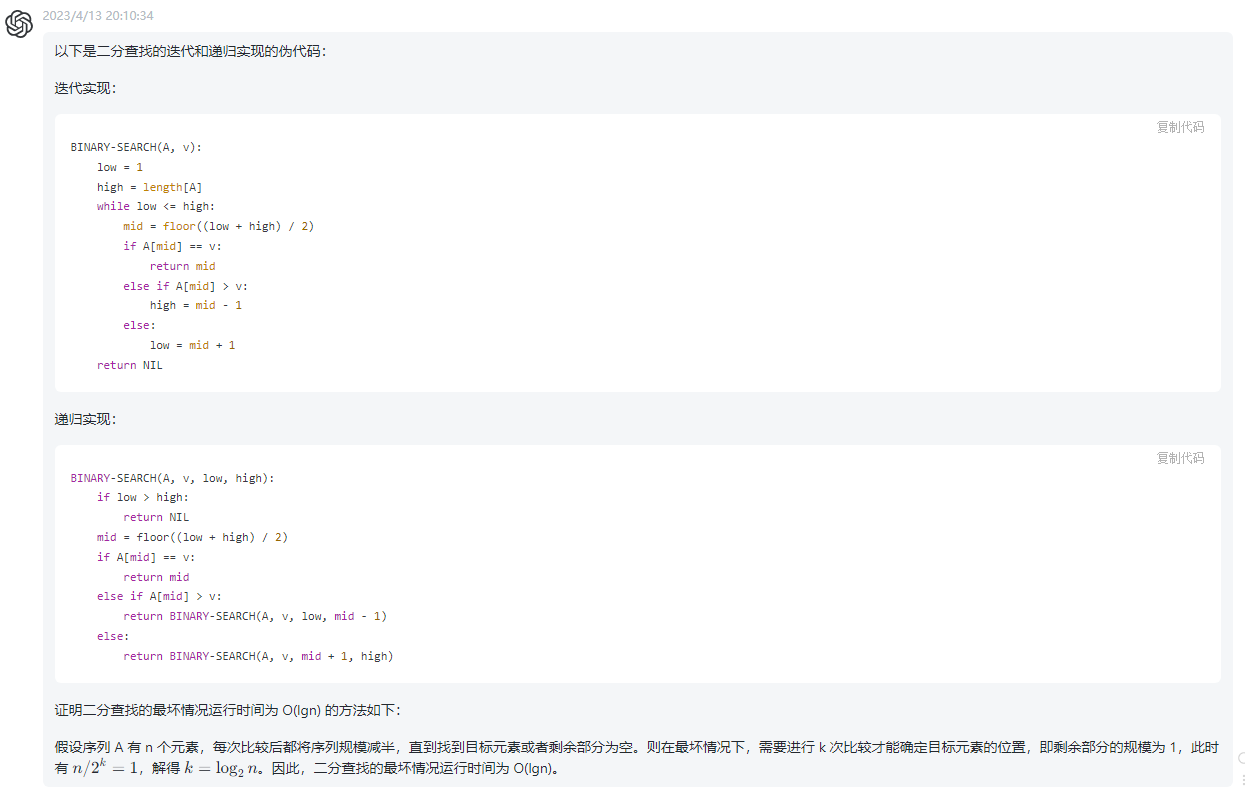
以下是二分查找的迭代和递归实现的伪代码：

迭代实现：

BINARY-SEARCH(A, v):
    low = 1
    high = length[A]
    while low <= high:
        mid = floor((low + high) / 2)
        if A[mid] == v:
            return mid
        else if A[mid] > v:
            high = mid - 1
        else:
            low = mid + 1
    return NIL

递归实现：

BINARY-SEARCH(A, v, low, high):
    if low > high:
        return NIL
    mid = floor((low + high) / 2)
    if A[mid] == v:
        return mid
    else if A[mid] > v:
        return BINARY-SEARCH(A, v, low, mid - 1)
    else:
        return BINARY-SEARCH(A, v, mid + 1, high)

证明二分查找的最坏情况运行时间为 O(lgn) 的方法如下：

假设序列 A 有 n 个元素，每次比较后都将序列规模减半，直到找到目标元素或者剩余部分为空。则在最坏情况下，需要进行 k 次比较才能确定目标元素的位置，即剩余部分的规模为 1，此时有 $n/2^k=1$，解得 $k={\log }_{2}n$。因此，二分查找的最坏情况运行时间为 O(lgn)。

六、注意到2.1节中的过程INSERTION-SORT的第5~7行的 while 循环采用一种线性查找来(反向)扫描已排好序的子数组 A[1…j-1]。我们可以使用二分查找(参见练习2.3-5)来把插人排序的最坏情况总运行时间改进到 O(nlgn)吗?

文心一言：

是的，可以使用二分查找来把插入排序的最坏情况总运行时间改进到 O(nlgn)。

在二分查找中，我们需要检查序列的中点是否等于要查找的元素，如果是，则返回中点的下标。否则，我们将序列剩余部分的规模减半，并递归地查找左半部分和右半部分。如果左半部分的下标小于要查找的元素的下标，则返回左半部分的下标；否则，返回右半部分的下标。

在插入排序中，我们需要将序列的中点与要查找的元素进行比较，如果中点等于要查找的元素，则返回中点的下标。否则，我们将序列剩余部分的规模减半，并递归地查找左半部分和右半部分。如果左半部分的下标小于要查找的元素的下标，则返回左半部分的下标；否则，返回右半部分的下标。

因此，二分查找的最坏情况运行时间为 O(nlgn)。

chatgpt：

是的，我们可以使用二分查找来将插入排序的最坏情况总运行时间改进到 O(nlgn)。

在插入排序算法中，第 i 次循环前，前 i-1 个元素已经排序完成。当处理第 i 个元素时，我们需要在已经排好序的前 i-1 个元素中，找到一个位置 j，使得 A[j]<=A[i]<A[j+1]，然后将第 i 个元素插入到 A[j+1] 处。

如果我们使用线性查找的方式，那么在最坏情况下，就需要扫描整个已排好序的子数组 A[1…j-1]，因此最坏情况下的比较次数为 1+2+…+(n-1)，即 O(n^2)。

但如果我们使用二分查找，在已经排好序的子数组 A[1…j-1] 中查找插入位置，我们只需要每次比较当前元素与子数组中间位置的元素，根据比较结果将查找范围缩小一半，这样就可以将查找的时间复杂度降低到 O(lgn)。因此，使用二分查找的插入排序算法的最坏情况总运行时间为 O(nlgn)。