讲故事环节：

在

~~一个风雪交加的夜晚~~

18世纪初普鲁士的哥尼斯堡，有一条河穿过，河上有两个小岛，有七座桥把两个岛与河岸联系起来。有个人提出一个问题：一个步行者怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点。后来大数学家欧拉把它转化成一个几何问题——一笔画问题。

大概就是这么个图

就是现在人们所说的一笔画问题

回归题目

上面这个图太乱了，根本无法分析

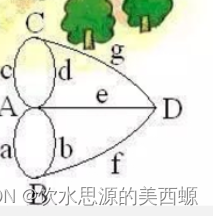
嗯~熟悉多了

~~难受多了~~

现在的问题就是，如果不重复且不遗漏地走过所有的边（点可以无限次走，没有限制）

~~当然不指望你把它证明出来（bushi）~~

我们的大数学家欧拉，找到了它的充要条件

1.奇点的数目不是0个就是2个

奇点：就是度为奇数（如果是有向图就是入读+出度=奇数），反之为偶点

概念：

无向图：

欧拉路：对于一个图，每条边可以且只能访问一次

欧拉回路：在欧拉图的情况下，最后要回到原点。也就是说欧拉路不一定是欧拉回路，但欧拉回路一定是欧拉路

欧拉路有且只有0或2个奇点，欧拉回路不能有奇点。如果一个连通图有2n个奇点，那么这个图最少要k笔完成

有向图：

欧拉路：至多一个顶点入度和出度相差为1，其他顶点入度和出度全部相同

欧拉回路：每个顶点入度和出度都一样

举个栗子：

假设一个图是一个“田”

每个拐角处都是一个点

按照上面说的，一个图有2n个奇点，这个图最少要k笔完成

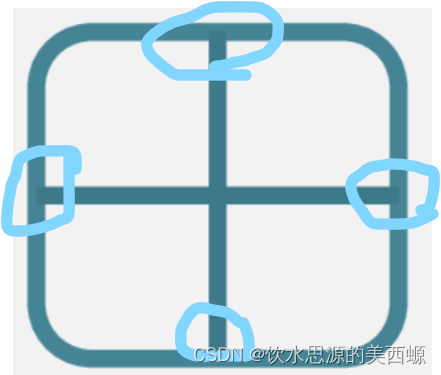
这个图一共四个奇点，所以至少需要2笔完成

解决方法：

1.dfs

第一步：判断图是否连通（不联通就啥也别说了）

第二步：判断奇点个数

很简单，但是使用dfs的话，就需要很多数组，并且用邻接矩阵是最方便的，所以费空间

2.并查集

分为G1和G2两个集合，G1表示已经联通的，G2表示未联通的

利用父亲表示法合并集合效率最高，也是上面那两步

代码：

并查集

#include<iostream>
using namespace std;

#define N 21

int e[N][N];
int du[N];
int total;
int path[405];
int pos;
int vis[N];
int n,m;

int father[N];
int h[N];

void make()
{
    for(int i=1;i<=n;i++)
    {
        h[i]=1;
        father[i]=i; 
    }   
}

int find(int a)
{
    if(father[a]!=a)
    {
        return father[a]=find(father[a]);
    }
    else
        return father[a];
}

void join(int a,int b)
{
   a=find(a);
   b=find(b);
   if(a==b) return;
   if(h[a]>=h[b]) 
   {
       father[b]=a;
       h[a]+=h[b];
       h[b]=0;
   }
   else if(h[a]<h[b])
   {
       father[a]=b;
       h[b]+=h[a];
       h[a]=0;
   }
}

void findpath(int s)
{
	for(int j=1;j<=n;j++)
	{
		if(e[s][j]==1)
		{
			e[s][j]=e[j][s]=0x7f;
			findpath(j);
		}
	}
	path[++pos]=s;
}

int main(){
	int a,b;
	cin>>n>>m;
	memset(e,0x7f,sizeof(e));
	make();


	for(int i=1;i<=m;i++)
	{
        cin>>a>>b;
		e[a][b]=e[b][a]=1;
        du[a]++;
		du[b]++;

		join(a,b);
	}

    int f=find(1);
	for(int i=2;i<=n;i++)
	{
        if(find(i)!=f)
		{
			cout<<"NO";
		    return 0;
		}
	}


	// if(h[f]!=n)
	// {
	// 	cout<<"NO";
	// 	return 0;
	// }

    total=0;
	int st=1;
	for(int i=1;i<=n;i++)
	{
		if(du[i]%2) 
		{
			total++;
			st=i;
		}
	}

	if(total!=0 && total!=2)
	{
		cout<<"NO";
		return 0;
	}

	findpath(st);


	for(int i=1;i<=pos;i++)
	{
		printf("%d ",path[i]);
	}
	
	return 0;
}

dfs深搜：


#include<iostream>
using namespace std;
#define N 21
int e[N][N];
int du[N];
int total;
int path[405];
int pos;
int vis[N];
int n,m;

void dfs(int i)
{
    vis[i]=true;
	total++;
	for(int j=1;j<=n;j++)
	{
		if(e[i][j]==1 && !vis[j]) 
		    dfs(j);
	}
}

void findpath(int s)
{
	for(int j=1;j<=n;j++)
	{
		if(e[s][j]==1)
		{
			e[s][j]=e[j][s]=0x7f;
			findpath(j);
		}
	}
	path[++pos]=s;
}

int main(){
	int a,b;
	cin>>n>>m;
	memset(e,0x7f,sizeof(e));
	for(int i=1;i<=m;i++)
	{
        cin>>a>>b;
		e[a][b]=e[b][a]=1;
        du[a]++;
		du[b]++;
	}

	dfs(1);
	if(total!=n)
	{
		cout<<"NO";
		return 0;
	}

    total=0;
	int st=1;
	for(int i=1;i<=n;i++)
	{
		if(du[i]&1) 
		{
			total++;
			st=i;
		}
	}
    
	if(total!=0 && total!=2) 
	{
		cout<<"NO";
		return 0;
	}

	findpath(st);

	for(int i=1;i<=pos;i++)
	{
		printf("%d ",path[i]);
	}

	return 0;
}

例题：

题目描述

如果一个无向图存在一笔画，则一笔画的路径叫做欧拉路，如果最后又回到起点，那这个路径叫做欧拉回路。

输入

第一行n，m，0 < n <=20，表示有n个点，m条边，以下m行描述每条边连接的两点。

输出

如果有欧拉路或欧拉回路，输出一条路径即可，顶点之间由空格隔开。

如果没有，输出NO

样例输入1

5 5
1 2
2 3
3 4
4 5
5 1

样例输出1

1 5 4 3 2 1