专栏导读

✍ 作者简介：i阿极，CSDN Python领域新星创作者，专注于分享python领域知识。

✍ 本文录入于《数据分析之术》，本专栏精选了经典的机器学习算法进行讲解，针对大学生、初级数据分析工程师精心打造，对机器学习算法知识点逐一击破，不断学习，提升自我。
✍ 订阅后，可以阅读《数据分析之术》中全部文章内容，详细介绍数学模型及原理，带领读者通过模型与算法描述实现一个个案例。
✍ 还可以订阅基础篇《数据分析之道》，其包含python基础语法、数据结构和文件操作，科学计算，实现文件内容操作，实现数据可视化等等。
✍ 其他专栏：《数据分析案例》，《机器学习案例》

1、KNN简介

KNN（K-Nearest Neighbors）算法是一种非参数的分类和回归算法，它可以用于解决分类和回归问题。

在KNN算法中，输入是一个向量，输出为该向量所属的类别或该向量的值。KNN算法的核心思想是：如果一个样本在特征空间中的K个最相邻的样本中，属于某一个类别的样本点最多，则该样本也属于这个类别。

在分类问题中，KNN算法的预测结果是通过所属类别最多的K个邻居来确定的。在回归问题中，KNN算法的预测结果是通过K个邻居的平均值来确定的。

KNN算法的实现步骤：

计算输入样本和训练样本之间的距离。
选取距离最近的K个样本点。
对于分类问题，将这K个样本点中出现次数最多的类别作为预测结果；对于回归问题，将这K个样本点的平均值作为预测结果。
输出预测结果。

KNN算法的优点是简单易懂，不需要对数据进行假设，对于非线性的数据集表现优秀，但是缺点也比较明显，需要存储所有的训练数据，计算距离时的计算量大，对异常值比较敏感，需要对数据进行归一化处理。同时，KNN算法对于高维数据集表现不佳，因为在高维数据空间中，样本点之间的距离容易产生偏差，从而影响预测的准确性。

2、KNN回归模型介绍

python中的sklearn模块提供了KNN算法实现分类和回归功能，该功能存在于子模块neighbors中，对于回归问题，需要调用KNeighborsRegressor类。

neighbors.KNeighborsRegressor(n_neighbors=5, weights='uniform', algorithm='auto', 
			           leaf_size=30, p=2, metric='minkowski', 
			           metric_params=None, n_jobs=1)

n_neighbors：用于指定近邻样本个数K，默认为5
weights：用于指定近邻样本的投票权重，默认为’uniform’，表示所有近邻样本的投票权重一样；如果为’distance’，则表示投票权重与距离成反比，即近邻样本与未知类别的样本点距离越远，权重越小，反之，权重越大
algorithm：用于指定近邻样本的搜寻算法，如果为’ball_tree’，则表示使用球树搜寻法寻找近邻样本；如果为’kd_tree’，则表示使用KD树搜寻法寻找近邻样本；如果为’brute’，则表示使用暴力搜寻法寻找近邻样本。默认为’auto’，表示KNN算法会根据数据特征自动选择最佳的搜寻算法
leaf_size：用于指定球树或KD树叶子节点所包含的最小样本量，它用于控制树的生长条件，会影响树的查询速度，默认为30
metric：用于指定距离的度量指标，默认为闵可夫斯基距离
p：当参数metric为闵可夫斯基距离时，p=1，表示计算点之间的曼哈顿距离；p=2，表示计算点之间的欧氏距离；该参数的默认值为2
metric_params：为metric参数所对应的距离指标添加关键字参数
n_jobs：用于设置KNN算法并行计算所需的CPU数量，默认为1表示仅使用1个CPU运行算法，即不使用并行运算功能

3、KNN模型应用-高炉发电量预测

3.1数据集信息：

该数据集包含 6 年（2006 年至 2011 年）从联合循环发电厂收集的 9568 个数据点，当时该发电厂被设置为满负荷工作。特征包括每小时平均环境变量温度 (T)、环境压力 (AP)、相对湿度 (RH) 和排气真空 (V)，以预测电厂每小时的净电能输出 (EP)。
联合循环发电厂 (CCPP) 由燃气轮机 (GT)、蒸汽轮机 (ST) 和热回收蒸汽发生器组成。在 CCPP 中，电力由结合在一个循环中的燃气轮机和蒸汽轮机产生，并从一个涡轮机转移到另一个涡轮机。虽然真空是从汽轮机收集并对其产生影响，但其他三个环境变量会影响 GT 性能。

3.2属性信息

温度 (T) 在 1.81°C 和 37.11°C 范围内，
环境压力 (AP) 在 992.89-1033.30 毫巴范围内，
相对湿度 (RH) 在 25.56% 至 100.16 范围内%
排气真空 (V) 在 25.36-81.56 cm Hg 范围内
每小时净电能输出 (EP) 420.26-495.76 MW

3.3数据准备

读取数据

# 读入数据
import pandas as pd
ccpp = pd.read_excel(r"D:\Download\CCPP\Folds5x2_pp.xlsx")
ccpp.head()

在这里插入图片描述
查看数据形状

# 返回数据集的行数与列数
ccpp.shape

在这里插入图片描述

3.4数据标准化和划分数据集

标准化

# 导入第三方包
from sklearn.preprocessing import minmax_scale
# 对所有自变量数据作标准化处理
predictors = ccpp.columns[:-1]
X = minmax_scale(ccpp[predictors])

将数据集拆分为训练集和测试集

# 将数据集拆分为训练集和测试集
from sklearn import model_selection
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, ccpp.PE, 
                                                                    test_size = 0.25, random_state = 1234)

3.5寻找最佳K值

设置不同K值，使用交叉验证寻找

# 设置待测试的不同k值
K = np.arange(1,np.ceil(np.log2(ccpp.shape[0]))).astype(int)
# 构建空的列表，用于存储平均MSE
mse = []
for k in K:
    # 使用10重交叉验证的方法，比对每一个k值下KNN模型的计算MSE
    cv_result = model_selection.cross_val_score(neighbors.KNeighborsRegressor(n_neighbors = k, weights = 'distance'), 
                                                X_train, y_train, cv = 10, scoring='neg_mean_squared_error')
    mse.append((-1*cv_result).mean())

将得到的最佳K值可视化

# 从k个平均MSE中挑选出最小值所对应的下标  
arg_min = np.array(mse).argmin()
# 绘制不同K值与平均MSE之间的折线图
plt.plot(K, mse)
# 添加点图
plt.scatter(K, mse)
# 添加文字说明
plt.text(K[arg_min], mse[arg_min] + 0.5, '最佳k值为%s' %int(K[arg_min]))
# 显示图形
plt.show()

在这里插入图片描述

3.6建立KNN模型预测

from sklearn import metrics
# 重新构建模型，并将最佳的近邻个数设置为7
knn_reg = neighbors.KNeighborsRegressor(n_neighbors = 7, weights = 'distance')
# 模型拟合
knn_reg.fit(X_train, y_train)
# 模型在测试集上的预测
predict = knn_reg.predict(X_test)
# 计算MSE值
metrics.mean_squared_error(y_test, predict)

在这里插入图片描述
真实值和预测值

# 对比真实值和预测值
pd.DataFrame({'Real':y_test,'Predict':predict}, columns=['Real','Predict']).head(10)

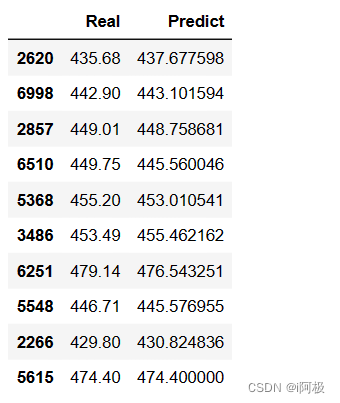
在这里插入图片描述

通过对比发现，KNN模型在测试集上的真实值和预测值非常接近，可以认为模型的拟合效果非常理想。

4、完整代码

# 读入数据
import pandas as pd
ccpp = pd.read_excel(r"D:\Download\CCPP\Folds5x2_pp.xlsx")
ccpp.head()

# 返回数据集的行数与列数
ccpp.shape

# 导入第三方包
from sklearn.preprocessing import minmax_scale
# 对所有自变量数据作标准化处理
predictors = ccpp.columns[:-1]
X = minmax_scale(ccpp[predictors])

# 将数据集拆分为训练集和测试集
from sklearn import model_selection
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, ccpp.PE, 
                                                                    test_size = 0.25, random_state = 1234)

import numpy as np
from sklearn import neighbors
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 设置待测试的不同k值
K = np.arange(1,np.ceil(np.log2(ccpp.shape[0]))).astype(int)
# 构建空的列表，用于存储平均MSE
mse = []
for k in K:
    # 使用10重交叉验证的方法，比对每一个k值下KNN模型的计算MSE
    cv_result = model_selection.cross_val_score(neighbors.KNeighborsRegressor(n_neighbors = k, weights = 'distance'), 
                                                X_train, y_train, cv = 10, scoring='neg_mean_squared_error')
    mse.append((-1*cv_result).mean())

# 从k个平均MSE中挑选出最小值所对应的下标  
arg_min = np.array(mse).argmin()
# 绘制不同K值与平均MSE之间的折线图
plt.plot(K, mse)
# 添加点图
plt.scatter(K, mse)
# 添加文字说明
plt.text(K[arg_min], mse[arg_min] + 0.5, '最佳k值为%s' %int(K[arg_min]))
# 显示图形
plt.show()

from sklearn import metrics
# 重新构建模型，并将最佳的近邻个数设置为7
knn_reg = neighbors.KNeighborsRegressor(n_neighbors = 7, weights = 'distance')
# 模型拟合
knn_reg.fit(X_train, y_train)
# 模型在测试集上的预测
predict = knn_reg.predict(X_test)
# 计算MSE值
metrics.mean_squared_error(y_test, predict)

# 对比真实值和实际值
pd.DataFrame({'Real':y_test,'Predict':predict}, columns=['Real','Predict']).head(10)