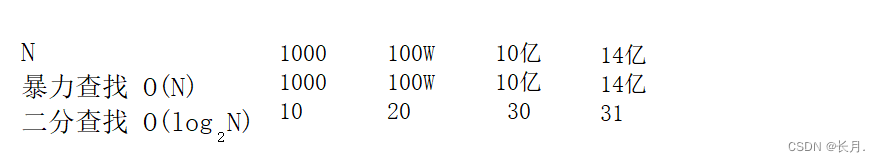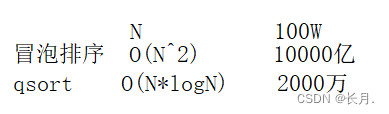文章目录
- 前言
- 1.什么是数据结构?
- 2.什么是算法?
- 3.时间复杂度
- 3.1 实例1:请计算一下Func1中++count语句总共执行了多少次?
- 大O的渐进表示法
- 实例2:计算Func2的时间复杂度
- 实例3:计算Func3的时间复杂度?
- 实例4:计算Func4的时间复杂度?
- 大O的渐进表示法总结
- 实例5:计算strchr的时间复杂度?
- 实例6:计算BubbleSort的时间复杂度?
- 实例7:二分查找的时间复杂度
- 实例8:计算阶乘递归Fac的时间复杂度
- 实例9:计算斐波那契递归Fib的时间复杂度
- 面试题:消失的数字
- 方法1.排序:依次查找,如果下一个数不是上一个数+1,那么上一个数字+1就是消失的数字
- 方法2.异或:相异为1,相同为0
- 方法3.0-N等差数列计算完整数组的和,减去缺失数字的数组里面的各个数字
- 总结
前言
1.什么是数据结构?
数据结构是计算机存储,组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合.
在内存中管理数据在这里插入图片描述
管理数据:增删查改
2.什么是算法?
算法就是定义良好的计算过程,它取一个或者一组值作为输入,并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果
比如说排序/二分查找
3.时间复杂度
1.算法的时间复杂度是一个数学函数式
2.算法中的基本操作的执行次数,为算法的时间复杂度
3.1 实例1:请计算一下Func1中++count语句总共执行了多少次?
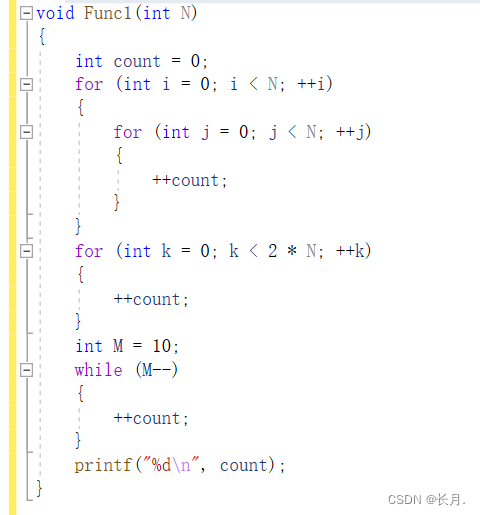
时间复杂度函数式:
F(N)=NN+2N+10
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
大O的渐进表示法


实例2:计算Func2的时间复杂度

O(N)
准确的来说是2N+10
但是当N无限大的时候,10忽略,N的系数倍和N本身是没有区别的
实例3:计算Func3的时间复杂度?

O(1)
注意O(1)不是代表1次,是代表常数次
实例4:计算Func4的时间复杂度?

O(1)
准确的来说是100,但是对于计算机来说常数的运算时间复杂度没有区别
大O的渐进表示法总结
1.用常数1取代运行时间中的所有加法常数。
2.在修改后的运行次数函数中,只保留最高阶项
3.如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶
实例5:计算strchr的时间复杂度?

相当于在字符数组里面查找一个字符的算法
whilw(*str){
if(*str==character)
return str;
else
++str;
}
另外有些算法的时间复杂度存在最好,平均和最坏的情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期待运行次数
最好情况:任意输入规模的最小运行数(下界)
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
(降低预期,底线思维)
实例6:计算BubbleSort的时间复杂度?

准确的时间复杂度:
第一趟 n-1次
第二塘 n-2次
第三趟 n-3次
…
4
3
2
1
每个次数构成一个等差数列,总次数=N*(N-1)/2
时间复杂度O(N^2)
实例7:二分查找的时间复杂度
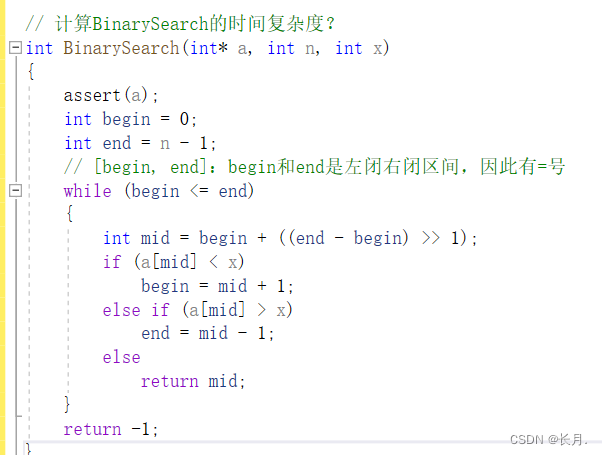
时间复杂度
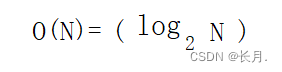
N/2/2/2/2…/2=1
假设找了x次,那么除了x个2
2^x=N
x=log2(N)
N代表数量级
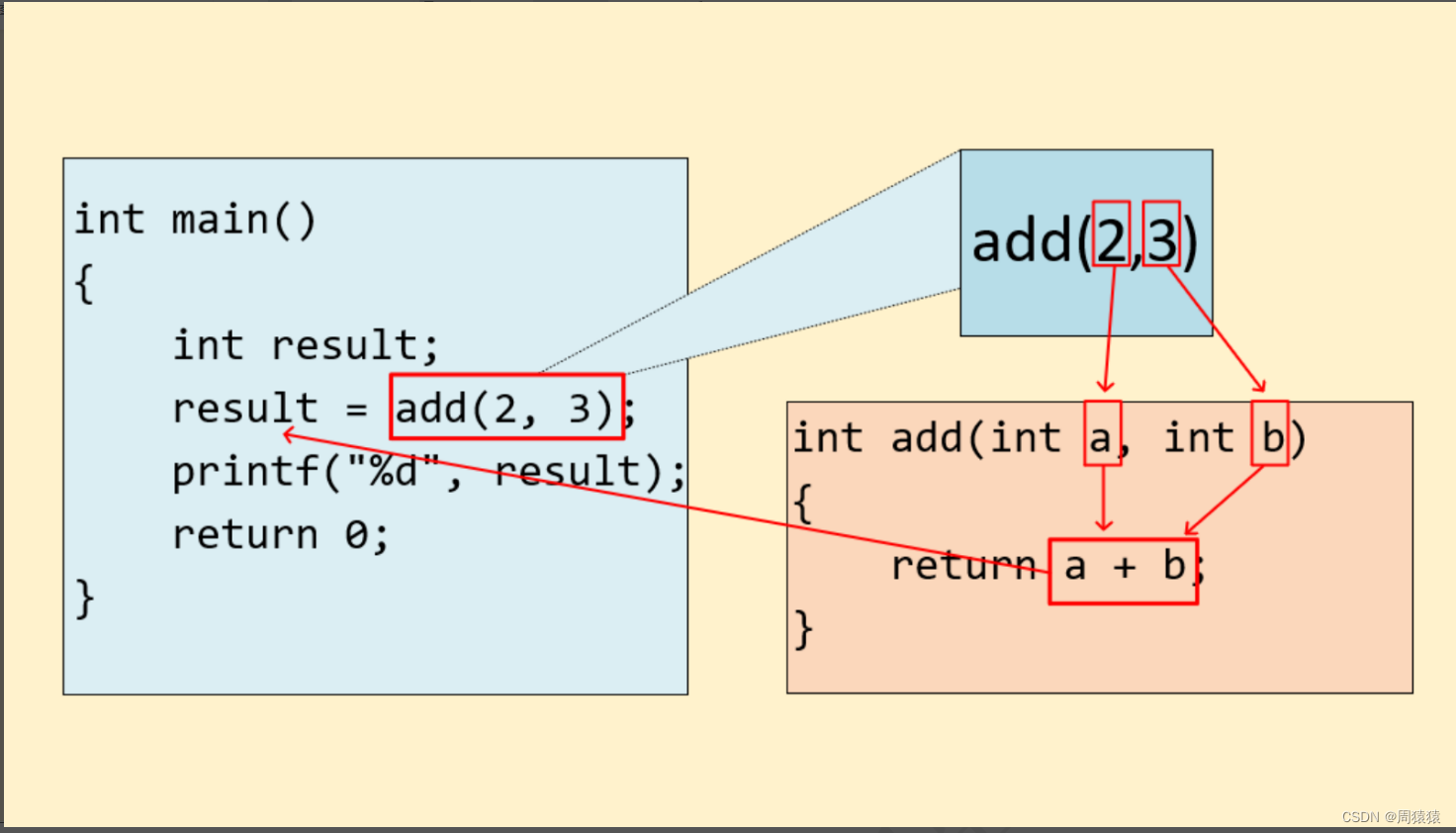
实例8:计算阶乘递归Fac的时间复杂度

答案是O(N)
Fac(N)
Fac(N-1)
Fac(N-2)
.
.
.
Fac(2)
Fac(1)
Fac(0)
总共调用了n+1次,每一次里面的时间复杂度是是O(1),加起来就是O(N)
变形

时间复杂度O(N^2)
每次调用的时候里面判断也可以算一次,但是可以忽略
实例9:计算斐波那契递归Fib的时间复杂度

时间复杂度为O(2^N)
面试题:消失的数字
数组nums包含从0到n的所有整数,但是其中缺了一个,请编写代码找出那个缺失的整数,你有办法在==O(N)==时间内完成吗?
方法1.排序:依次查找,如果下一个数不是上一个数+1,那么上一个数字+1就是消失的数字
冒泡排序的话时间复杂度是O(n^2)
qsort排序的话是O(NlogN)
需要用一个循环来判断如果下一个数不是上一个数+1,那么上一个数字+1就是消失的数字,准确地来说时间复杂度是O(NlogN+N),最后的N可以忽略掉,所以时间复杂度是O(N*logN).
时间复杂度都不满足题目的要求,所以这道题目不能使用排序
方法2.异或:相异为1,相同为0
思路分析
用一个数字x跟0~n的数字异或,再和缺失数字的数组异或
异或的特点:
参与运算的两个值,如果两个值相同,则结果为1,不同为1
(1)0 ^ 0=0 0 ^ 1=1
0和任何数异或=任何数
(2)1^0=1 1 ^1=0
1异或任何数=任何数取反
(3)任何数异或自己相当于把自己本身置0
题目分析:
1.将x置为0,让它去异或现有的缺失数字的数组里面的各个数字,结果保存到x中
2.再用上一步得到的x去异或原本完整的数组里面的各个元素,根据异或的特点,相同的两个数之间异或结果为0,那么最终两个数组相同的数字异或完之后剩下0去异或原来完整的数组中没有匹配到的数字(也就是消失的数字),结果就是消失的数字
画图讲解:
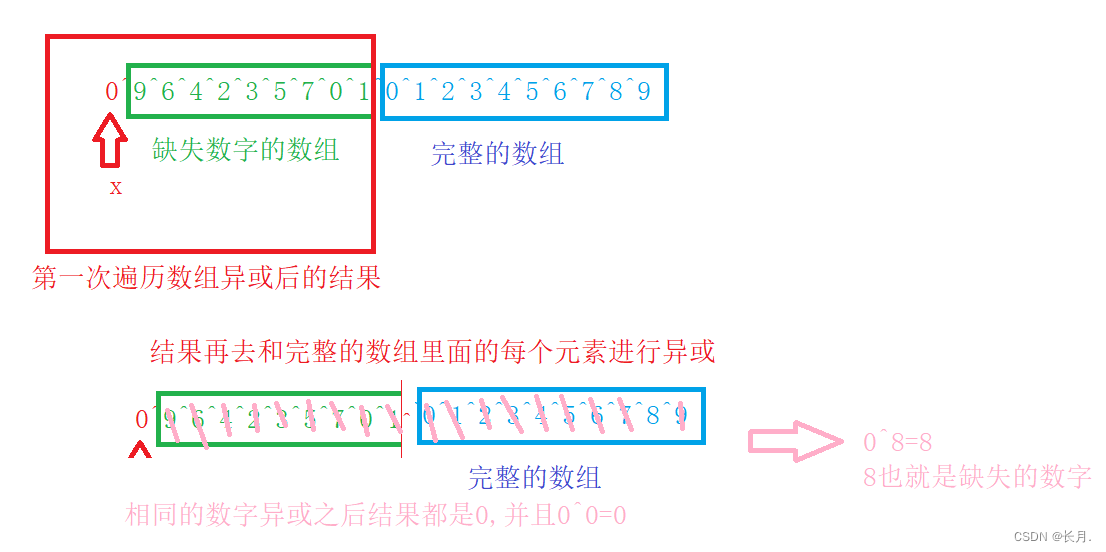
0 1 2 3 4 5 6 7 8 9
假设x就是消失的数字
假设x=0
0和任何数字异或,结果是任何数
先和第一个缺失数字的数组异或,遍历数组的时间复杂度是O(N)
再和第二个完整的数组异或,时间复杂度是O(N+1)
总的来说这个方法的时间复杂度是O(N+N+1)也就是O(2*N+1)
时间复杂度实际上还是O(N)
注意:
异或满足交换律
1 1 2异或和1 2 1 异或的结果相同
int missingNumber(int* nums, int numsSize) {
int x = 0; //和数组里面的每个值异或
for (int i = 0; i < numsSize; ++i)
{
x ^= nums[i];
}
for (int i = 0; i < numsSize; i++) {
x ^= i;
}
return x;
}
方法3.0-N等差数列计算完整数组的和,减去缺失数字的数组里面的各个数字
等差数列求和的时间复杂度是O(1)
减数组里面的值需要遍历一遍,时间复杂度是O(N)
这个方法的时间复杂度是O(N+1)也就是O(N)
#include<stddef.h> //size_t是C标准在stddef.h中定义的,size_t类型表示C中任何对象所能达到的最大长度,它是无符号整数
//size_t在32位系统上定义为unsigned int,也就是32位无符号整型.
//size_t在64位系统上定义为unsigned int,也就是64位无符号整型.
int missingNumber(int* nums, int numsSize) {
int x = (0 + numsSize) * (numsSize+1) / 2;
for (size_t i = 0; i < numsSize; i++) {
x -= nums[i];
}
return x;
}
总结
今天的学习内容就到这里啦,如果对友友们有帮助的话,记得点赞收藏博客,关注后续的数据结构学习内容分享哦~👻👻