目录
1 与栈有关的考题
1.1 最小栈
1.2 栈的弹出压入序列
1.3 逆波兰表达式求值
1.4 二叉树的最近公共祖先
1.5 单调栈
2 与队列有关的考题
2.1 二叉树的分层遍历
2.2 滑动窗口
1 与栈有关的考题
1.1 最小栈
题目描述:

解题思路:
要想在O(1)时间内获得栈内最小元素只用一个栈肯定是行不通的,所以我们不妨再开一个栈来记录当前栈里面每个元素的最小值,这样就要多开出O(N)的空间,可以优化空间的方法是并不是所有的元素都要入最小栈,而是当前元素比最小栈栈顶的数据大便不必再入数据了,但是等于时一定要入进去,当pop掉元素时只需要比较普通栈与最小栈栈顶元素是否相等,若相等,则最小栈栈顶数据也得pop。
参考代码:
class MinStack {
public:
MinStack() {}
void push(int val) {
_st.push(val);
if(_minSt.empty() || _minSt.top()>=val)
_minSt.push(val);
}
void pop() {
if(_minSt.top()==_st.top())
_minSt.pop();
_st.pop();
}
int top() {
return _st.top();
}
int getMin() {
return _minSt.top();
}
stack<int> _st;
stack<int> _minSt;//记录最小的数据
};运行结果:
题后反思:
万一数据像这种22222222,貌似我们优化空间的方法起不到作用了,可以采取的优化措施是我们存储数据时可以存一个pair,里面额外记录一下变量的个数,当有重复数据时便不再入数据了,而是++里面的计数器,pop时就--里面的计数器,大家有兴趣可以自己实现下,这里我就不再实现了。
1.2 栈的弹出压入序列
题目描述:

解题思路:
这道题的解决方法有很多种,这里分享一种比较容易理解的思路:另外搞一个栈,将栈的压入序列不断的push到这个栈中,当该栈不为空并且栈的弹出序列与该栈栈顶数据相等时就pop掉该栈栈顶数据,然后不断迭代走,最后返回值就是该栈是否为空或者是否走到了弹出序列的尾。
参考代码:
class Solution {
public:
bool IsPopOrder(vector<int> pushV,vector<int> popV) {
stack<int> v;
int pushi=0,popi=0;
while(pushi<pushV.size())
{
v.push(pushV[pushi++]);
while(!v.empty() && v.top()==popV[popi])
{
v.pop();
popi++;
}
}
return v.empty();
}
};运行结果:
1.3 逆波兰表达式求值
题目描述:

解题思路:
由于逆波兰表达式就是后缀表达式,运算符的优先级已经确定了,所以我们只需要模拟下运算的过程即可,注意先取的数据是右,后取的数据为左。
参考代码:
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> s;
for(auto& e:tokens)
{
if(e=="+" || e=="-" || e=="*" || e=="/")
{
int right=s.top();
s.pop();
int left=s.top();
s.pop();
switch(e[0])
{
case '+':
s.push(left+right);
break;
case '-':
s.push(left-right);
break;
case '*':
s.push(left*right);
break;
case '/':
s.push(left/right);
break;
}
}
else
{
s.push(stoi(e));
}
}
return s.top();
}
};运行结果:
题后反思:
假如给的不是后缀表达式,而是中缀表达式,如何将中缀表达式转化为后缀表达式呢?
给定中缀表达式【1+2*(3-4)+5/6】,我们如何将其转化为后缀表达式?
基本规则是这样的:当遇到操作数的时候我们直接输出;遇到操作符当栈为空就直接入栈,栈若不为空就与栈顶数据相比,若优先级大于栈顶就将该操作符入栈(由于后面操作符优先级可能更大,所以先让其入栈),若优先级小于或者等于栈顶,就将栈顶数据pop掉然后输出,直到栈为空或者遇到优先级更小的操作符,然后继续迭代直到访问到所有元素。
但是这个规则只适用于没有()的转换中,例如【1+2*3-4】可以转化成【1 2 3 * + 4 -】
但是像上面的那个栗子【1+2*(3-4)+5/6】貌似就不适用了,处理方法有两种:
- 第一种是不入()到栈中,当发现出现了()时就认为()中的运算符优先级非常大,就让其入栈,其他规则与基本规则类似。
- 第二种是将()入栈,当出现(时就认为(的优先级非常低,(目的是让括号中运算符入栈),当出现)时同样认为)的优先级非常低,(目的是让括号中运算符出栈输出)
无论使用哪种规则,我们都能够很轻易的将上述中缀表达式转化为:
【1 2 3 4 - * + 5 6 / +】
1.4 二叉树的最近公共祖先
题目描述:
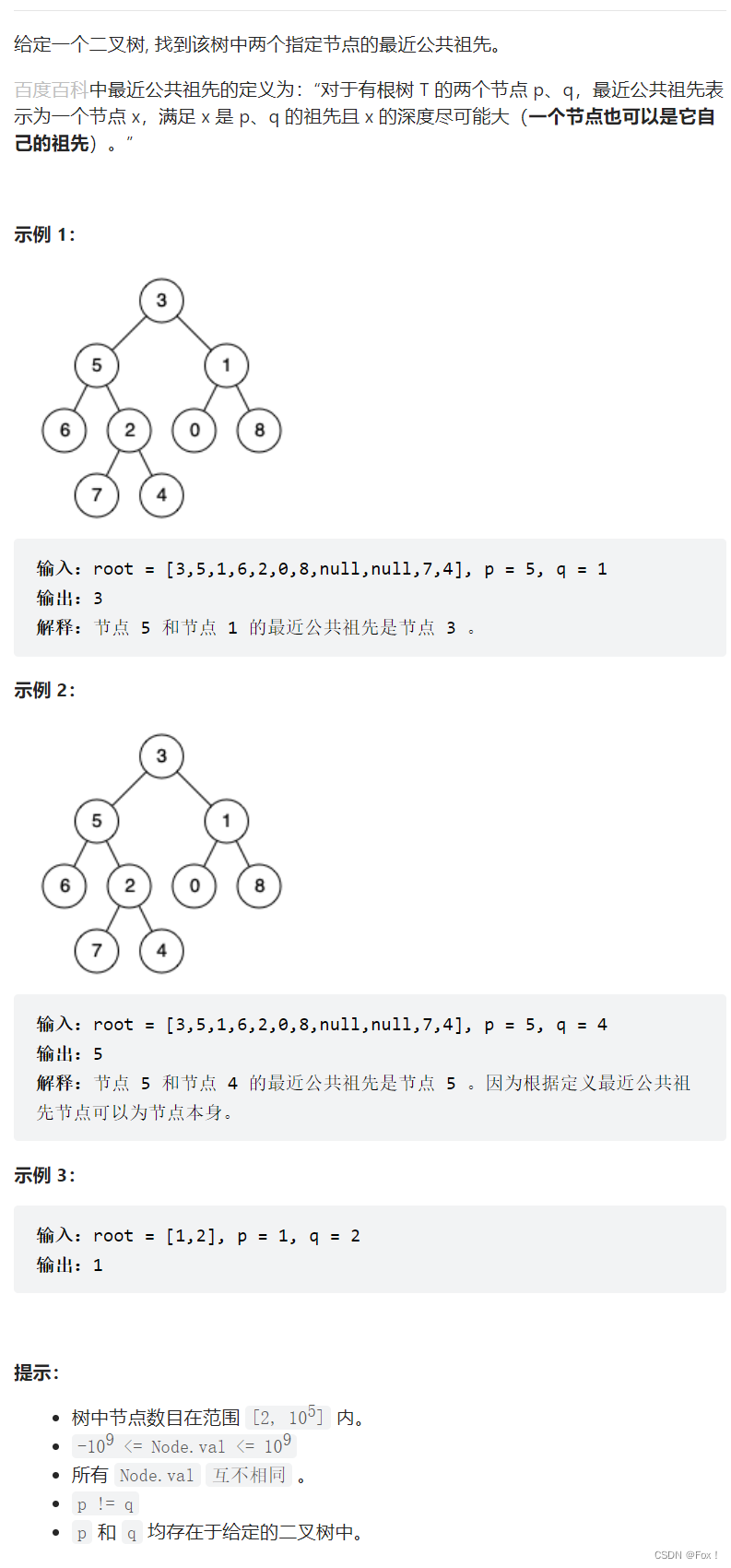
解题思路1:
基本思路是通过根节点的左子树和右子树分别找p和q,然后再递归去找。
参考代码:
class Solution {
public:
bool find(TreeNode* root, TreeNode* x)
{
if(root==nullptr)
return false;
if(root==x)
return true;
return find(root->left,x) || find(root->right,x);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==nullptr)
return nullptr;
if(root==p || root==q)
return root;
bool pInLeft,pInRight,qInLeft,qInRight;
pInLeft=find(root->left,p);
pInRight=!pInLeft;
qInLeft=find(root->left,q);
qInRight=!qInLeft;
if((pInLeft && qInRight) || (pInRight && qInLeft))
return root;
else if(pInLeft && qInLeft)
return lowestCommonAncestor(root->left,p,q);
else if(pInRight && qInRight)
return lowestCommonAncestor(root->right,p,q);
else
return nullptr;
}
};题后反思:
这种方式如果该树大致是一个单叉树时效率就很低下了,这样时间复杂度大概是N^2量级的,有什么更好的解决思路吗?
解题思路2:
我们可以用两个栈来分别存储查找p和q的路径,然后转化为链表相交问题,这样时间复杂度是N量级的。
参考代码:
class Solution {
public:
//记录路径,最坏情况也是O(N)
bool findPath(TreeNode* root, TreeNode* x, stack<TreeNode*>& Path)
{
if(root==nullptr)
return false;
Path.push(root);//先把结点入进去
if(root==x)
return true;
if(findPath(root->left,x,Path))//如果从左子树中找到了就返回
return true;
if(findPath(root->right,x,Path))//如果从右子树中找到了就返回
return true;
//走到这里说明左子树没有找到,右子树也没有找到,就pop掉栈顶
Path.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
stack<TreeNode*> pPath;
stack<TreeNode*> qPath;
findPath(root,p,pPath);
findPath(root,q,qPath);
//让大的先走差距步
while(pPath.size()!=qPath.size())
{
if(pPath.size()>qPath.size())
pPath.pop();
else
qPath.pop();
}
while(pPath.top()!=qPath.top())
{
pPath.pop();
qPath.pop();
}
return pPath.top();
}
};运行结果:
1.5 单调栈
题目描述:

解题思路:
单调栈模型,相信大家能够轻松AC.
参考代码:
自己写一个栈:
#include<iostream>
using namespace std;
const int N=1e5+10;
int st[N],tt;
int main()
{
int n;
scanf("%d",&n);
while(n--)
{
int x;
scanf("%d",&x);
while(tt && st[tt]>=x) tt--;
if(!tt) printf("-1 ");
else printf("%d ",st[tt]);
st[++tt]=x;
}
return 0;
}使用STL中stack:
#include<iostream>
#include<stack>
using namespace std;
int main()
{
int n;
scanf("%d",&n);
stack<int> st;
while(n--)
{
int x;
scanf("%d",&x);
while(!st.empty() && st.top()>=x) st.pop();
if(st.empty()) printf("-1 ");
else printf("%d ",st.top());
st.push(x);
}
return 0;
}2 与队列有关的考题
2.1 二叉树的分层遍历
题目描述:
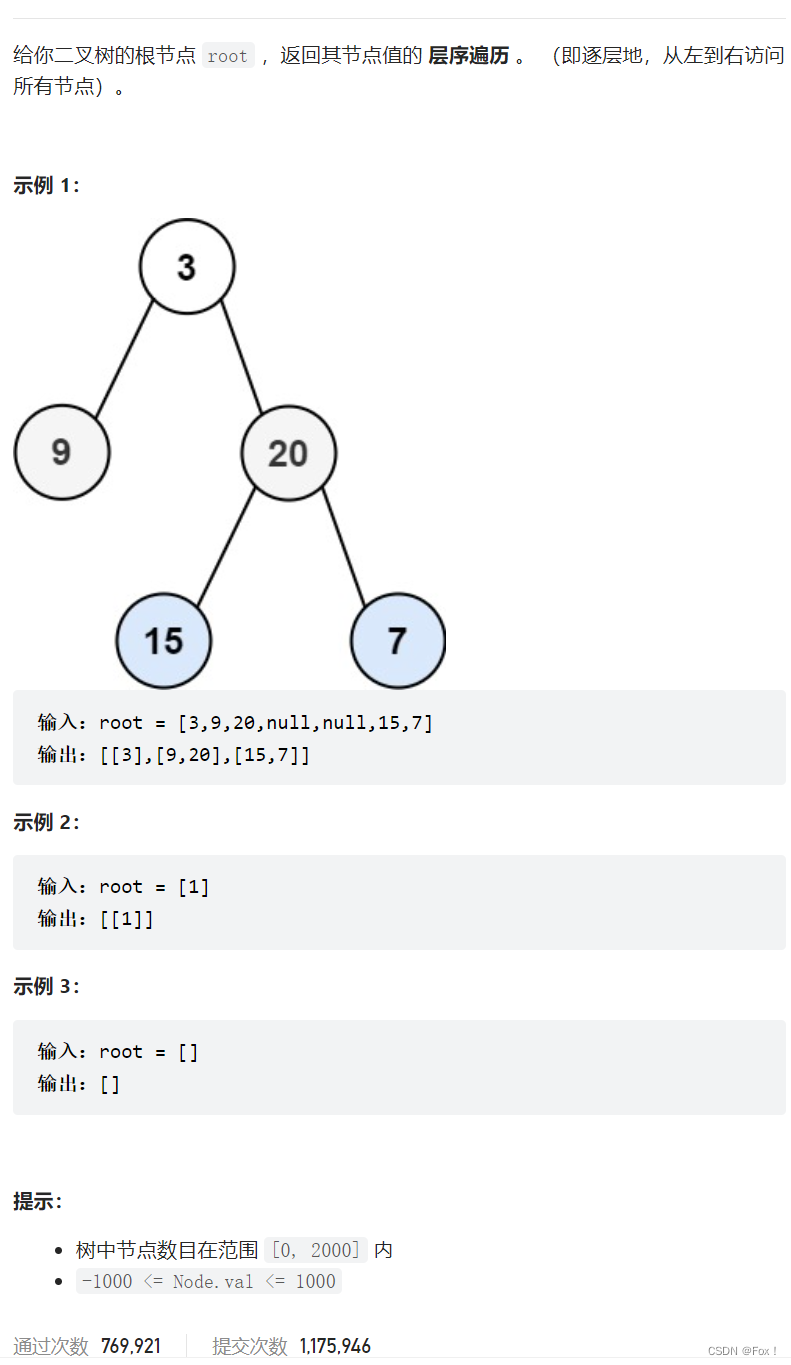
解题思路:
这种题我们能一眼看出来是用队列做,但是本题的难点在于怎样确定每层结点个数。我们不妨用一个变量levelSize计数每层结点个数,当pop掉该层结点push新的结点后及时更新levelSize。
参考代码:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> vv;
queue<TreeNode*> q;
if(root==nullptr)
return vv;
int levelSize=1;
q.push(root);
while(!q.empty())
{
vector<int> v;
while(levelSize--)
{
TreeNode* front=q.front();
v.push_back(front->val);
q.pop();
if(front->left)
q.push(front->left);
if(front->right)
q.push(front->right);
}
levelSize=q.size();
vv.push_back(v);
}
return vv;
}
};
2.2 滑动窗口
题目描述:
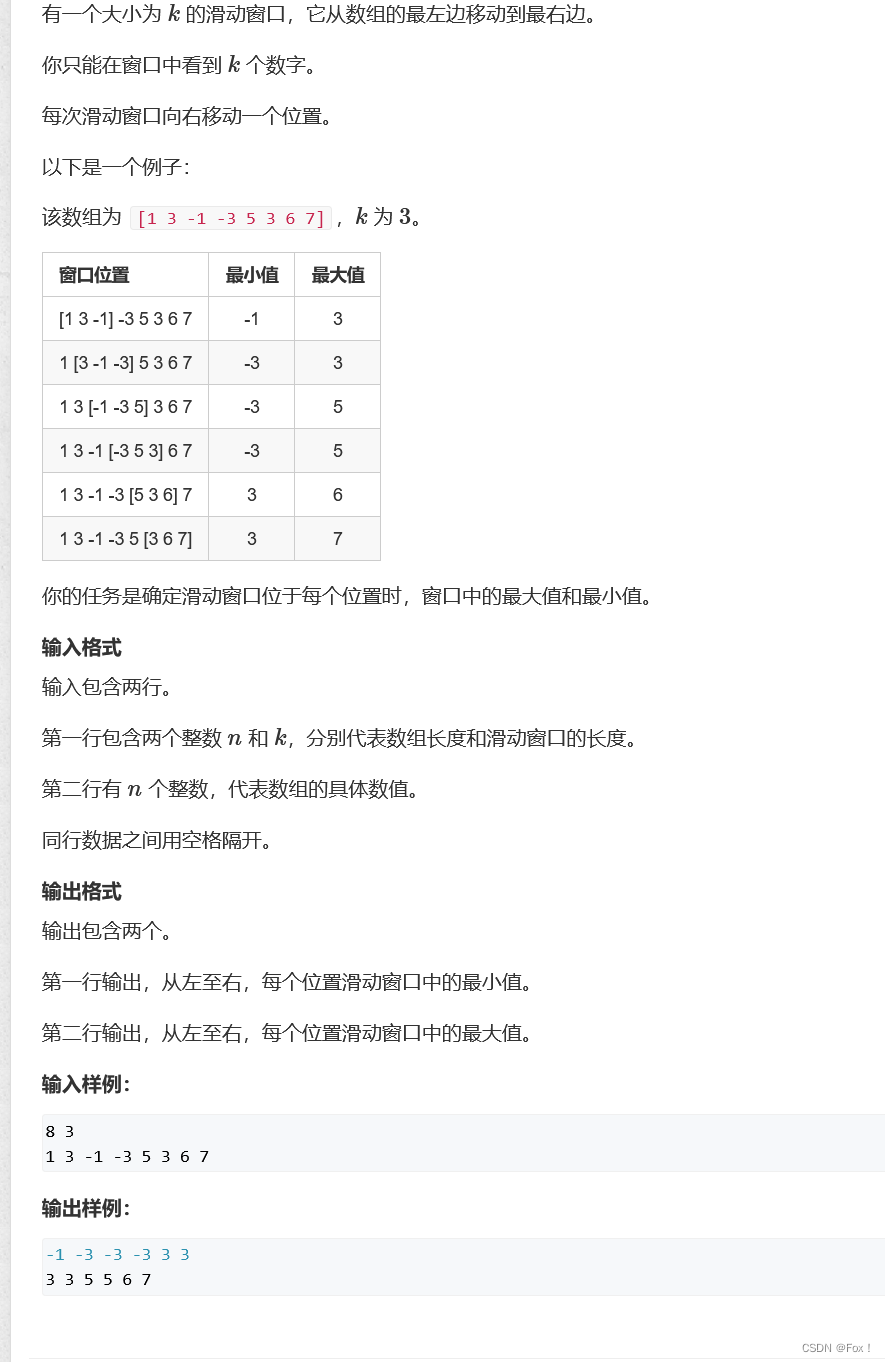
解题思路:
这也是一个简单的基础模板题,就直接给大家看代码了。
自己实现一个:
#include<iostream>
using namespace std;
const int N=1e6+10;
int a[N],q[N];
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
int hh=0,tt=-1;
for(int i=0;i<n;i++)
{
if(hh<=tt && i-m+1>q[hh]) ++hh;//q[hh]不在窗口[i-m,i-1]内就出队
while(hh<=tt && a[i]<=a[q[tt]]) --tt;//当前值<=队尾值,队尾出队(双端队列)
q[++tt]=i;//队列中入的是下标目的是为了方便队头出队
if(i-m+1>=0) printf("%d ",a[q[hh]]);//使用队头(最小值)
}
puts("");
hh=0,tt=-1;
for(int i=0;i<n;i++)
{
if(hh<=tt && i-m+1>q[hh]) ++hh;
while(hh<=tt && a[i]>=a[q[tt]]) --tt;
q[++tt]=i;
if(i-m+1>=0) printf("%d ",a[q[hh]]);
}
}采用STL的deque(双端队列):
#include<iostream>
#include<deque>
using namespace std;
const int N=1e6+10;
int a[N];
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
deque<int>q;//双向队列
for(int i=0;i<n;i++)
{
if(!q.empty() && i-m+1>q.front()) q.pop_front();
while(!q.empty() && a[i]<=a[q.back()]) q.pop_back();
q.push_back(i);
if(i-m+1>=0) printf("%d ",a[q.front()]);
}
puts("");
q.clear();//记得要清理
for(int i=0;i<n;i++)
{
if(!q.empty() && i-m+1>q.front()) q.pop_front();
while(!q.empty() && a[i]>=a[q.back()]) q.pop_back();
q.push_back(i);
if(i-m+1>=0) printf("%d ",a[q.front()]);
}
return 0;
}