基本介绍

PyTorch Geometric

PyG（PyTorch Geometric）是一个基于PyTorch的库，可以轻松编写和训练图神经网络（GNN），用于与结构化数据相关的广泛应用。

它包括从各种已发表的论文中对图和其他不规则结构进行深度学习的各种方法，也称为几何深度学习。此外，它还包括易于使用的迷你批处理加载程序，用于在许多小型和单巨型图上操作，多GPU支持，大量通用基准数据集（基于创建自己的简单接口），GraphGym实验管理器，以及有用的转换，既用于在任意图上学习，也用于在3D网格或点云上学习。

安装PyG可以参考我的博客：python安装pyg（pytorch_geometric）的两种方式：https://wang11.blog.csdn.net/article/details/128987042

图卷积神经网络GCN

GCN由Thomas N. Kipf和Max Welling在ICLR2017提出。

Semi-Supervised Classification with Graph Convolutional Networks： https://arxiv.org/abs/1609.02907

对于一个输入图，他有N个节点，每个节点的特征组成一个特征矩阵X，节点与节点之间的关系组成一个邻接矩阵A，X和A即为模型的输入。

GCN是一个神经网络层，它具有以下逐层传播规则：
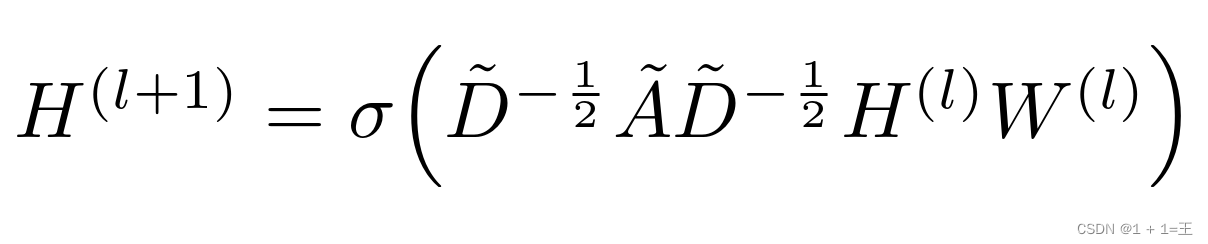
在这里插入图片描述

其中，

˜A = A + I，A为输入图的领接矩阵，I为单位矩阵。
˜D为˜A的度矩阵，˜D_ii = ∑_j ˜A_ij
H是每一层的特征，对于输入层H = X
σ是非线性激活函数
W为特定层的可训练权重矩阵

节点分类任务实现

Cora数据集

Cora数据集包含2708篇科学出版物，5429条边，总共7种类别。数据集中的每个出版物都由一个 0/1 值的词向量描述，表示字典中相应词的缺失/存在。该词典由 1433 个独特的词组成。意思就是说每一个出版物都由1433个特征构成，每个特征仅由0/1表示。它是在Semi-Supervised Learning with Graph Embeddings项目中生成的，可以用于可视化和分析节点之间的连接关系。

Cora数据集的特点包括：

每个出版物都由一个0/1值的词向量描述，表示字典中相应词的缺失/存在。
该词典由1433个独特的词组成。
数据集包含以下文件：
ind.cora.x：训练集节点特征向量，保存对象为：scipy.sparse.csr.csr_matrix，实际展开后大小为：(140，1433)
ind.cora.tx：测试集节点特征向量，保存对为：scipy.sparse.csr.csr_matrix，实际展开后大小为：(1000，1433)
ind.cora.allx：包含有标签和无标签的训练节点特征向量，保存对象为： scipy.sparse.csr.csr_matrix，实际展开后大小为：(1708，1433)
ind.cora.y：one-hot表示的训练节点的标签，保存对象为：numpy.ndarray
ind.cora.ty：one-hot表示的测试节点的标签，保存对象为：numpy.ndarray
ind.cora.ally：one-hot表示的ind.cora.allx对应的标签，保存对象为：numpy.ndarray。

使用PyG加载Cora数据集：

from torch_geometric.datasets import Planetoid
from torch_geometric.transforms import NormalizeFeatures

dataset = Planetoid(root='data/Planetoid', name='Cora', transform=NormalizeFeatures())
data = dataset[0]
print(data)

在这里插入图片描述

print(data.x)	# 节点特征矩阵[2708,1433]
print(data.y)	# 节点类别
print(data.edge_index)	# 边
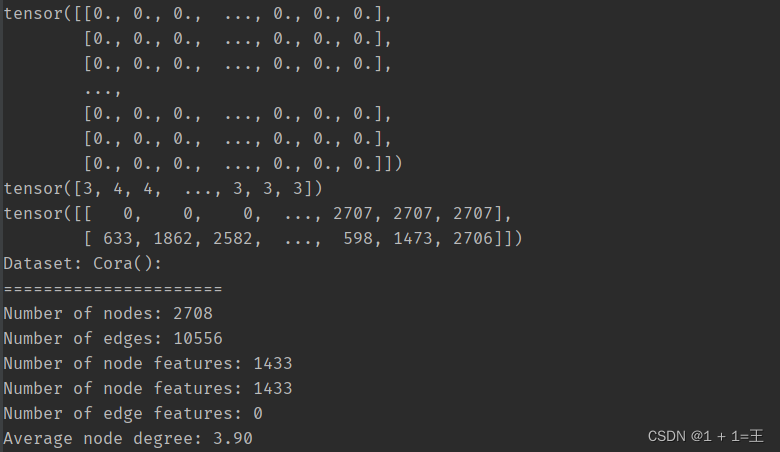
print(f'Dataset: {dataset}:')
print('======================')
print(f'Number of nodes: {data.num_nodes}')  # 节点数量
print(f'Number of edges: {data.num_edges}')  # 边数量
print(f'Number of node features: {data.num_node_features}')  # 节点特征维度
print(f'Number of node features: {data.num_features}')  # 节点特征维度
print(f'Number of edge features: {data.num_edge_features}')  # 边特征维度
print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}')  # 平均节点度

在这里插入图片描述

搭建GCN模型

class GCN(torch.nn.Module):
    def __init__(self, in_channels, hidden_channels, out_channels):
        super().__init__()

        self.conv1 = GCNConv(in_channels, hidden_channels)
        self.conv2 = GCNConv(hidden_channels, out_channels)

    def forward(self, x, edge_index):
        x = self.conv1(x, edge_index)
        x = x.relu()
        x = F.dropout(x, p=0.5, training=self.training)
        x = self.conv2(x, edge_index)
        return x
# 输入通道数：dataset.num_features=1433，即节点特征维度
# 输出通道数：dataset.num_classes=7，即节点类别数
model = GCN(dataset.num_features, 16, dataset.num_classes)

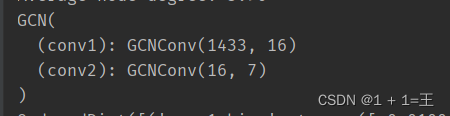
在这里插入图片描述

定义损失函数

criterion = torch.nn.CrossEntropyLoss()  # Define loss criterion.

定义优化器

optimizer = torch.optim.Adam(model.parameters(), lr=0.01)  # Define optimizer.

优化器选择Adam，学习率设置为0.01。

训练与测试

训练

def train():
    model.train()
    optimizer.zero_grad()
    out = model(data.x, data.edge_index)
    loss = criterion(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()
    return loss

测试

def test():
    model.eval()
    out = model(data.x, data.edge_index)
    pred = out.argmax(dim=1)
    test_correct = pred == data.y	# 计算分类正确的节点数
    test_acc = int(test_correct.sum()) / int(data.num_nodes)	# 计算正确率
    return test_acc

迭代并输出

e, l, acc = [], [], []
for epoch in range(1, 201):
    loss = train()
    a = test()
    e. append(epoch)
    l.append(loss)
    acc.append(a)
    print(f'Epoch: {epoch:03d}, Acc: {a:04f}, Loss: {loss:.4f}')
matplotlib.rc("font", family='FangSong')
plt.plot(e, l, color='red', linewidth=2, linestyle="solid", label='loss')
plt.plot(e, acc, color='green', linewidth=2, linestyle="solid", label='acc')
plt.legend()
plt.xlabel("epoch")
plt.show()

其中，定义了两个列表l和acc分别用于存储每轮迭代的损失值和准确率，便于后续使用plt可视化输出。
迭代训练过程可视化：
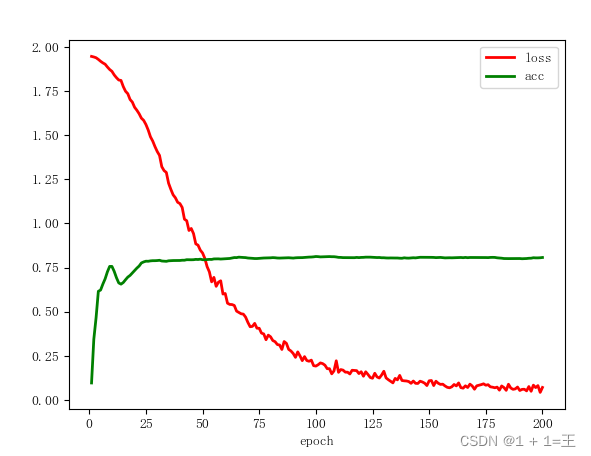
在这里插入图片描述
经过200次迭代训练分类准确率达到0.8左右，CELoss由1.9将至0.05左右并趋于收敛。

完整代码

import matplotlib
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from torch_geometric.nn import GCNConv
import torch.nn.functional as F
from torch_geometric.datasets import Planetoid
from torch_geometric.transforms import NormalizeFeatures


class GCN(torch.nn.Module):
    def __init__(self, in_channels, hidden_channels, out_channels):
        super().__init__()

        self.conv1 = GCNConv(in_channels, hidden_channels)
        self.conv2 = GCNConv(hidden_channels, out_channels)

    def forward(self, x, edge_index):
        x = self.conv1(x, edge_index)
        x = x.relu()
        x = F.dropout(x, p=0.5, training=self.training)
        x = self.conv2(x, edge_index)
        return x


dataset = Planetoid(root='data/Planetoid', name='Cora', transform=NormalizeFeatures())
data = dataset[0]
print(data)

print(data.x)	# 节点特征矩阵[2708,1433]
print(data.y)	# 节点类别
print(data.edge_index)	# 边
print(f'Dataset: {dataset}:')
print('======================')
print(f'Number of nodes: {data.num_nodes}')  # 节点数量
print(f'Number of edges: {data.num_edges}')  # 边数量
print(f'Number of node features: {data.num_node_features}')  # 节点特征维度
print(f'Number of node features: {data.num_features}')  # 节点特征维度
print(f'Number of edge features: {data.num_edge_features}')  # 边特征维度
print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}')  # 平均节点度


model = GCN(dataset.num_features, 16, dataset.num_classes)

print(model)
criterion = torch.nn.CrossEntropyLoss()  # Define loss criterion.
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)  # Define optimizer.

# 训练
def train():
    model.train()
    optimizer.zero_grad()
    out = model(data.x, data.edge_index)
    loss = criterion(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()
    return loss

# 测试
def test():
    model.eval()
    out = model(data.x, data.edge_index)
    pred = out.argmax(dim=1)
    test_correct = pred == data.y
    test_acc = int(test_correct.sum()) / int(data.num_nodes)
    return test_acc


e, l, acc = [], [], []
for epoch in range(1, 201):
    loss = train()
    a = test()
    e. append(epoch)
    l.append(loss)
    acc.append(a)
    print(f'Epoch: {epoch:03d}, Acc: {a:04f}, Loss: {loss:.4f}')
matplotlib.rc("font", family='FangSong')
plt.plot(e, l, color='red', linewidth=2, linestyle="solid", label='loss')
plt.plot(e, acc, color='green', linewidth=2, linestyle="solid", label='acc')
plt.legend()
plt.xlabel("epoch")
plt.show()