核心思想

  本文提出一种联合图学习和图匹配的算法（GLAM），将图的构建和匹配过程整合到一个端到端的注意力网络中。相比于其他启发式的建图方法，如Delaunay三角法、KNN方法或完全图，通过学习构建的图结构能够更加准确的反映关键点之间的语义关系。与SuperGlue和NCTR类似，本文也采用了自注意力层和交叉注意力层进行信息传递和聚合，但做了两个改进：1.将位置特征向量与每个注意力层输出的特征向量相加，来充分利用关键点的位置信息；2. 在交叉注意力层中计算注意力权重时，使用Sinkhorn算子取代了softmax层。这样一来不需要专门的匹配层，最后一个交叉注意力层输出的结果就可以作为一个柔性的匹配关系矩阵。

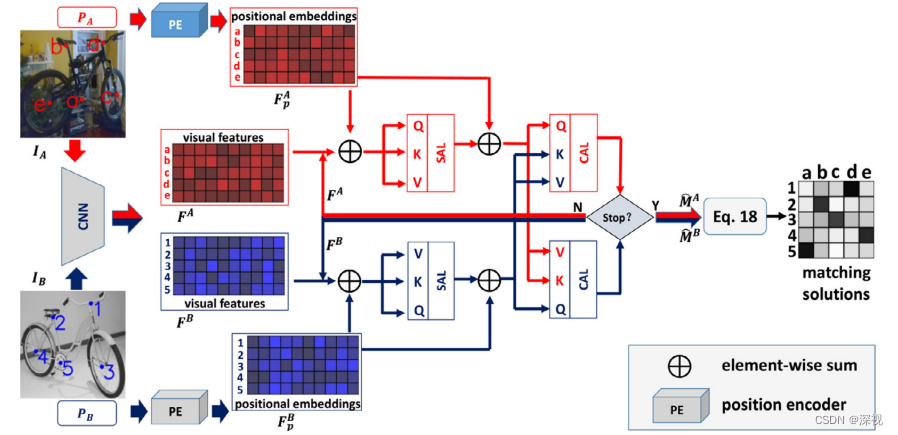
实现过程

  首先，利用一个卷积神经网络分别提取两幅图中关键点对应的视觉特征$F^A,F^B$，通过一个多层感知机$\rho$提取关键点坐标$P^A,P^B$中包含的位置特征$\rho (P^A),\rho (P^B)$，将视觉特征和位置特征逐元素相加，得到输入特征$F^A=F^A+\rho (P^A)$，图$B$相同。
  输入的特征将进入注意力层进行信息的传递和聚合，注意力层包含自注意力层和交叉注意力层具体的计算过程不再赘述，大家可以参考这篇博文的介绍。在原有的注意力机制的基础上作者做了两点改进。第一就是将位置特征$\rho (P^A),\rho (P^B)$分别加到每个注意力层的输出中，我觉得这一步是有必要的，因为没有预先构建图结构，因此需要借助位置信息来反映了节点之间结构关系，这在许多的图像关键点匹配中都是成立的。第二个改进是在交叉注意力层中使用sinkhorn算子取代了Softmax层来计算注意力权重。具体而言，常用的注意力权重计算方法如下

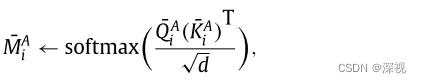
而本文采用的是

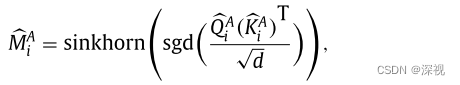
其中$sgd$表示的是Sigmoid层，目的是将向量归一化到$(0,1)$，来满足sinkhorn算子输入的非负性要求。softmax层相当于逐行进行归一化，而Sinkhorn算子是逐行逐列进行归一化。实验表明在源图和目标图中关键点数量一致时，这个方法是有效的，而如果关键点数量不一致，则需要对源图的关键点和目标图的关键对应的注意力权重分别做逐行归一化和逐列归一化。
  由于交叉注意力层的计算中已经使用sinkhorn算子进行归一化处理了，因此不需要专门设计一个匹配网络来进行匹配矩阵计算，只需要利用最后一层交叉注意力层的中间输出值来计算

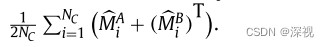
$N_C$表示交叉注意力层中的头（head）的数量。损失函数方面，作者将匹配问题看作一个二元分类问题，采用加权交叉熵损失函数

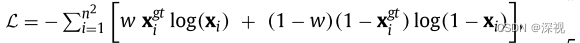
$w$表示权重系数，${\mathbf{x}}^{gt}，\mathbf{x}$分别为真实的匹配关系矩阵${\mathbf{X}}^{gt}$和预测的匹配关系矩阵$\mathbf{X}$的向量化表示。

创新点

• 将位置特征添加到每个注意力层的输出中
• 在交叉注意力层中使用sinkhorn算子取代了Softmax层来计算注意力权重

算法总结

  本文整体来讲延续了SuperGlue开创的基于注意力机制的图匹配方法，两点改进虽然简单但也是有效的。至于作者提到的图学习和图匹配的结合，其实是隐式地通过注意力机制实现的，节点之间的注意力权重就反映了连接的强度，也就是边的权重，这个在其他基于注意力机制的图匹配方法中其实都是类似的。作者在实验环节，专门展示了通过学习得到关联矩阵和人工标记的关联矩阵非常接近，说明学习得到的图结构能够更加准确的反映节点之间的语义关系。并且使用本文得到的图结构取代其他图匹配的方法中的启发式建图方法，均能有效的提高匹配效果。这说明图结构中所蕴含的归纳偏置信息对于图匹配是至关重要的，构建一个好的图结构能够有效的提高匹配准确性。