【POJ No. 3321】 子树查询 Apple Tree
北大OJ 题目地址
【题意】
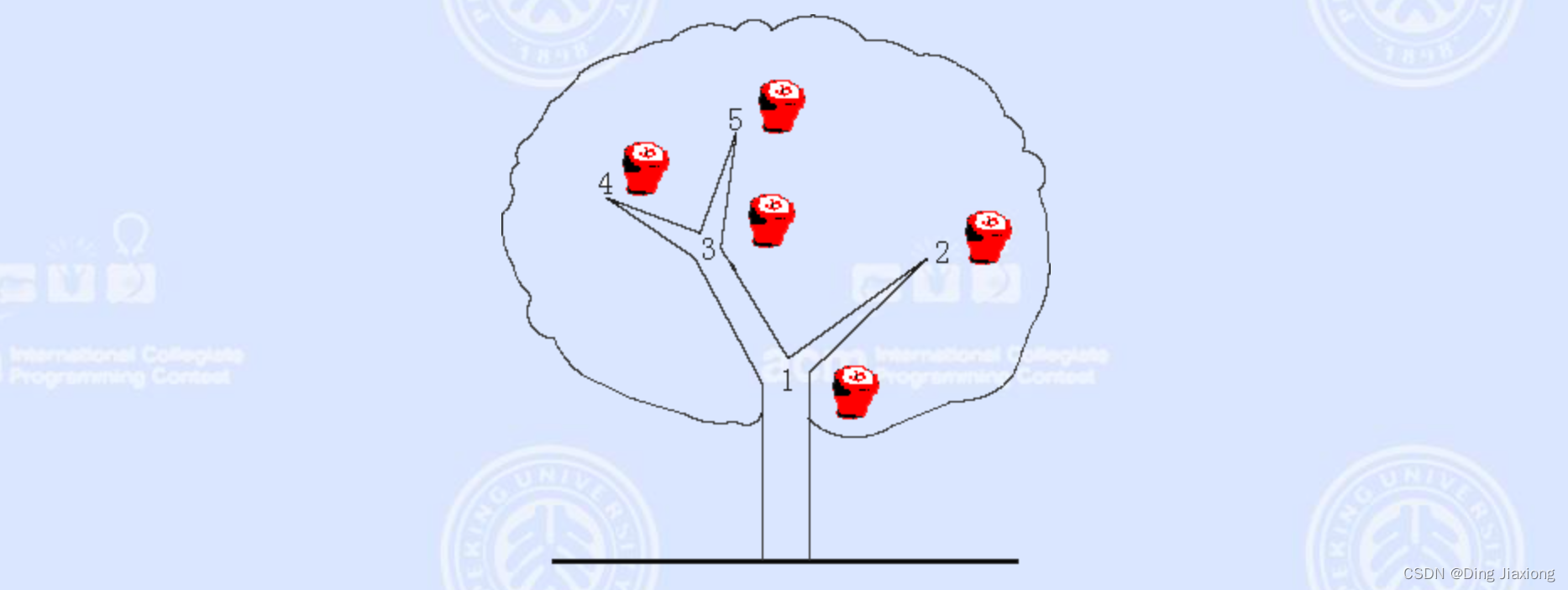
在卡卡的房子外面有一棵苹果树,树上有N 个叉(编号为1~N ,根为1),它们通过分支连接。苹果在叉上生长,两个苹果不会在同一个叉上生长。一个新的苹果可能会在一个空叉上长出来,卡卡还可能会从树上摘一个苹果作为他的甜点。
卡卡想了解一棵子树上有多少苹果。
【输入输出】
输入:
第1行包含一个整数N (N ≤100,000),表示树中叉的数量。以下N -1行,每行都包含两个整数u 和v ,表示叉u 和叉v 通过分支连接。下一行包含整数M (M ≤100,000)。以下M 行,每行都包含一个消息,C x 表示改变x 叉上的苹果状态。若叉上有苹果,则卡卡会选择摘掉它,否则一个新的苹果在这个空叉上长大;Q x 表示查询x 叉上方子树中的苹果数量,包括x 叉上的苹果(若存在)。
注意:开始时树上长满了苹果。
输出:
对每个查询,都单行输出答案。
【样例】

【思路分析】
本题包含两种操作,一种是点更新,一种是查询以当前节点为根的子树的苹果数量。
点更新很简单,那么如何得到以当前节点为根的子树的苹果数量呢?
若将一棵树深度遍历,则记录遍历时当前节点进来和出去时的序号,两个序号之间的节点就是当前节点的子树节点。可以利用DFS序将子树转换为序列,然后求解区间和。
【算法设计】
① 根据输入的分支构建树。
② 采用深度遍历求树的DFS序列,记录进出i 节点的序号L[i ]和R[i ]。
③ Q x :查询以x 节点为根的子树中的苹果数量,只需计算进出x 节点的区间和[L[x ], R[x ]],即sum(R[x ])-sum(L[x ]-1)。
④ C x :若判断x 节点的值为1,则在树状数组中点更新-1,否则+1。然后a [x ]^=1,进行异或运算,1变为0,0变为1。
【举个栗子】
输入数据如下。

① 构建一棵树,深度优先遍历的dfs序列如下图所示。
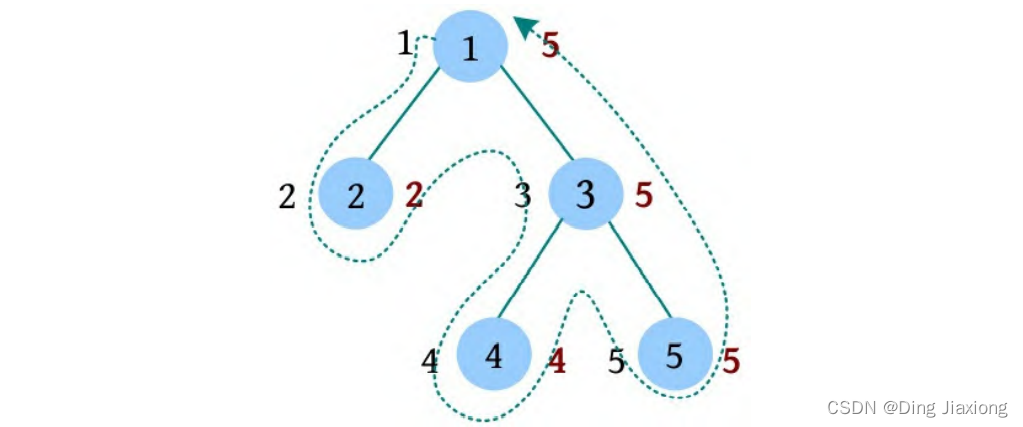
② 节点i 进来和出去时的序号如下:

③ 查询或更新操作。
-
Q 1:查询以1号节点为根的子树中的苹果数量。1号节点的进出序号为L[1]=1,R[1]=5,查询[1, 5]的区间和,sum(R[1])-sum(L[1]-1)=5-0=5,所以1号节点的子树中的苹果数量为5。
-
Q 3:查询以3号节点为根的子树中的苹果数量。3号节点的进出序号为L[3]=3,R[3]=5,查询[3, 5]的区间和,sum(R[3])-sum(L[3]-1)=5-2=3。所以3号节点的子树中的苹果数量为3。
-
C 2:改变2号节点的苹果状态。2号节点有苹果(值为1),在树状数组中点更新-1,然后a [2]^=1,进行异或运算,1变为0,0变为1,此时a [2]=0。
-
Q 1:查询以1号节点为根的子树中的苹果数量,1号节点的进出序号为L[1]=1、R[1]=5,查询[1, 5]的区间和,sum(R[1])-sum(L[1]-1)=4-0=5。所以1号节点的子树中的苹果数量为4。
【算法实现】
#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int maxn=1e5+10;
int N,q;
int c[maxn];
int a[maxn];
int L[maxn],R[maxn];
int head[maxn];
int cnt;
int dfn;
struct edge{
int u,v;
int next;
}E[2*maxn];
void adde(int u,int v){
E[++cnt].u=u;
E[cnt].v=v;
E[cnt].next=head[u];
head[u]=cnt;
}
int lowbit(int x){
return x&(-x);
}
void add(int i,int v){
for(;i<=N;i+=lowbit(i))
c[i]+=v;
}
int sum(int i){
int ans=0;
for(;i>0;i-=lowbit(i)){
ans+=c[i];
}
return ans;
}
void init(){
memset(c,0,sizeof(c));
memset(L,0,sizeof(L));
memset(R,0,sizeof(R));
memset(head,0,sizeof(head));
cnt=0;
dfn=1;
for(int i=1;i<=N;i++){
a[i]=1;
add(i,1);
}
}
void dfs(int u,int fa){
L[u]=dfn++;
for(int i=head[u];i;i=E[i].next){
int v=E[i].v;
if(v==fa) continue;
dfs(v,u);
}
R[u]=dfn-1;
}
int main(){
scanf("%d",&N);
int u,v;
init();
for(int i=1;i<N;i++){
scanf("%d%d",&u,&v);
adde(u,v);
}
dfs(1,1);
scanf("%d",&q);
char op[10];
for(int i=1;i<=q;i++){
scanf("%s %d",op,&v);
if(op[0]=='C'){
if(a[L[v]])
add(L[v],-1);
else
add(L[v],1);
a[L[v]]^=1;
}
else{
int s1=sum(R[v]);
int s2=sum(L[v]-1);
printf("%d\n",s1-s2);
}
}
return 0;
}