HQChart实战教程60-如何定制十字光标输出内容

news2025/1/11 7:52:51

HQChart实战教程60-如何定制十字光标输出内容

  • 十字光标
    • 效果图
  • 步骤：
    • 1. 注册事件
    • 2. 外部格式化输出内容
      • Y 轴输出说明
      • X轴输出说明
  • HQChart插件源码地址
  • 完整的demo源码

十字光标

当鼠标或手势在K线上移动的时候， 会出现一个十字线，已经X轴和Y轴对应数值的输出。X轴输出日期+时间 ， Y轴输出当前的数值。有时候我们需要指定输出的内容，HQChart支持自定义输出的文字及颜色 如下图。

效果图

在这里插入图片描述

步骤：

1. 注册事件

如何注册事件见教程 HQChart使用教程5- K线图控件操作函数说明‘

<

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/420274.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

2.1.1网络io与io多路复用select/poll/epoll

2.1.1网络io与io多路复用select/poll/epoll

关于网络io&#xff0c;我们可以通过一个服务端-客户端的示例来了解&#xff1a; 这是一段TCP服务端的代码&#xff1a; #include <stdio.h> #include <errno.h> #include <string.h> #include <unistd.h> #include <sys/socket.h> #include &l…
阅读更多...
Android系统启动流程--zygote进程的启动流程

Android系统启动流程--zygote进程的启动流程

在上一篇init进程启动流程中已经提到&#xff0c;在init中会解析一个init.rc文件&#xff0c;解析后会执行其中的命令来启动zygote进程、serviceManager进程等&#xff0c;下面我们来看一下&#xff1a; //文件路径&#xff1a;system/core/init/init.cppstatic void LoadBoot…
阅读更多...
电子商务转化率对你来说有多重要？

电子商务转化率对你来说有多重要？

有许多电子商务企业遇到了瓶颈期&#xff0c;低转化率并不总是表明您的业务出了大问题&#xff0c;但它们确实表明您可以做得更多&#xff0c;赚得更多。在文中&#xff0c;我们将讨论电子商务转化率对你的重要性&#xff0c;以及提高电子商务转化率的最佳久经考验的方法。 一、…
阅读更多...
如何选择IT培训机构？

如何选择IT培训机构？

作为学习IT技术的一种方式、平台&#xff0c;培训班存在已久。而作为国内培训机构的老大哥&#xff0c;北大青鸟于1999年成立&#xff0c;是IT职业教育的开创者&#xff0c;专注于软件、网络、营销等各个IT技术领域&#xff0c;为IT行业输送了奖金百万技术人才。24年以来&#…
阅读更多...
网络编程学习，项目er图

网络编程学习，项目er图

https://note.youdao.com/s/FEoXGdFe 思路&#xff1a;将每位上的数存放在一个数组里&#xff0c;每次从最高位开始遍历&#xff0c;先找到最大的位数&#xff0c;再根据是否为0&#xff0c;得到要加的数 网络编程是使用Java语言编写网络应用程序的过程。Java提供了一系列API&…
阅读更多...
操作系统作业 18-22章

操作系统作业 18-22章

第十八章 1.根据题中所给参数计算线性页表大小和不同情况下的变化 paging-linear-translate.py -P 1k -a 1m -p 512m -v -n 0 paging-linear-translate.py -P 1k -a 2m -p 512m -v -n 0 paging-linear-translate.py -P 1k -a 4m -p 512m -v -n 0 页大小为1kb&#xff0c;地址空…
阅读更多...
Git详细教程，彻底理解Git运作机制

Git详细教程，彻底理解Git运作机制

Git详细教程前言git常用命令版本管理远程仓库分支管理正文git版本管理版本回退工作区和暂存区工作区版本库&#xff08;Repository&#xff09;撤销修改删除文件git远程仓库github使用添加远程库小结从远程库克隆git分支管理创建和合并分支git merge vs git rebase解决冲突第一…
阅读更多...
即视角｜元宇宙社交：新瓶旧酒 or 老树新芽？

即视角｜元宇宙社交：新瓶旧酒 or 老树新芽？

即视角 Insight 共享即构新洞察&#xff0c;共建行业新动能——ZEGO即构科技基于音视频技术领域的多年深耕&#xff0c;综合面向各行业的服务经验&#xff0c;在【即视角】栏目发布即构对行业的洞察。 近期我们将聚焦于#元宇宙商业化#话题&#xff0c;共分为三篇&#xff1a;…
阅读更多...
自从上了数据结构课之后就想自学c++了

自从上了数据结构课之后就想自学c++了

所以今天是摆烂的第三天&#xff1a; 就是来总结一下自己刚学c常犯的小错误&#xff08;在注释里&#xff09;和总结吧&#xff1b; 先来看看hello world输出代码&#xff1b; //打了四遍这个代码终于对了TAT //在一整个程序里面如果有多个文件并且不止一个main函数的话&…
阅读更多...
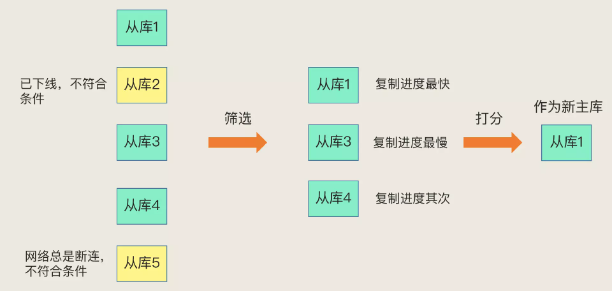
聊聊Redis sentinel 机制

聊聊Redis sentinel 机制

Redis 的哨兵机制自动完成了以下三大功能&#xff0c;从而实现了主从库的自动切换&#xff0c;可以降低 Redis 集群的运维开销&#xff1a; 监控主库运行状态&#xff0c;并判断主库是否客观下线&#xff1b;在主库客观下线后&#xff0c;选取新主库&#xff1b;选出新主库后&…
阅读更多...
C语言函数大全-- j 开头的函数

C语言函数大全-- j 开头的函数

C语言函数大全 本篇介绍C语言函数大全– j 开头的函数 1. j0&#xff0c;j0f 1.1 函数说明 函数声明函数功能double j0 (double x);计算 x 的 第一类 0 阶贝塞尔函数&#xff08;double&#xff09;float j0f (float x);计算 x 的 第一类 0 阶贝塞尔函数&#xff08;float&…
阅读更多...
AndroidNDK开发——使用Cmake编译生成so文件

AndroidNDK开发——使用Cmake编译生成so文件

文章目录AndroidNDK开发——使用Cmake编译生成so文件1.添加Cmake文件&#xff1a;2.添加Cmake依赖&#xff1a;3.jni文件如下&#xff1a;4.Android.mk文件&#xff1a;5.Application.mk文件6.SerialPort.c文件&#xff1a;7.SerialPort.h文件&#xff1a;8.运行项目&#xff1…
阅读更多...
剑指 Offer II 049. 从根节点到叶节点的路径数字之和

剑指 Offer II 049. 从根节点到叶节点的路径数字之和

中等题题目 &#xff1a; 给定一个二叉树的根节点 root &#xff0c;树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表一个数字&#xff1a; 例如&#xff0c;从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。计算从根节点到叶节点生…
阅读更多...
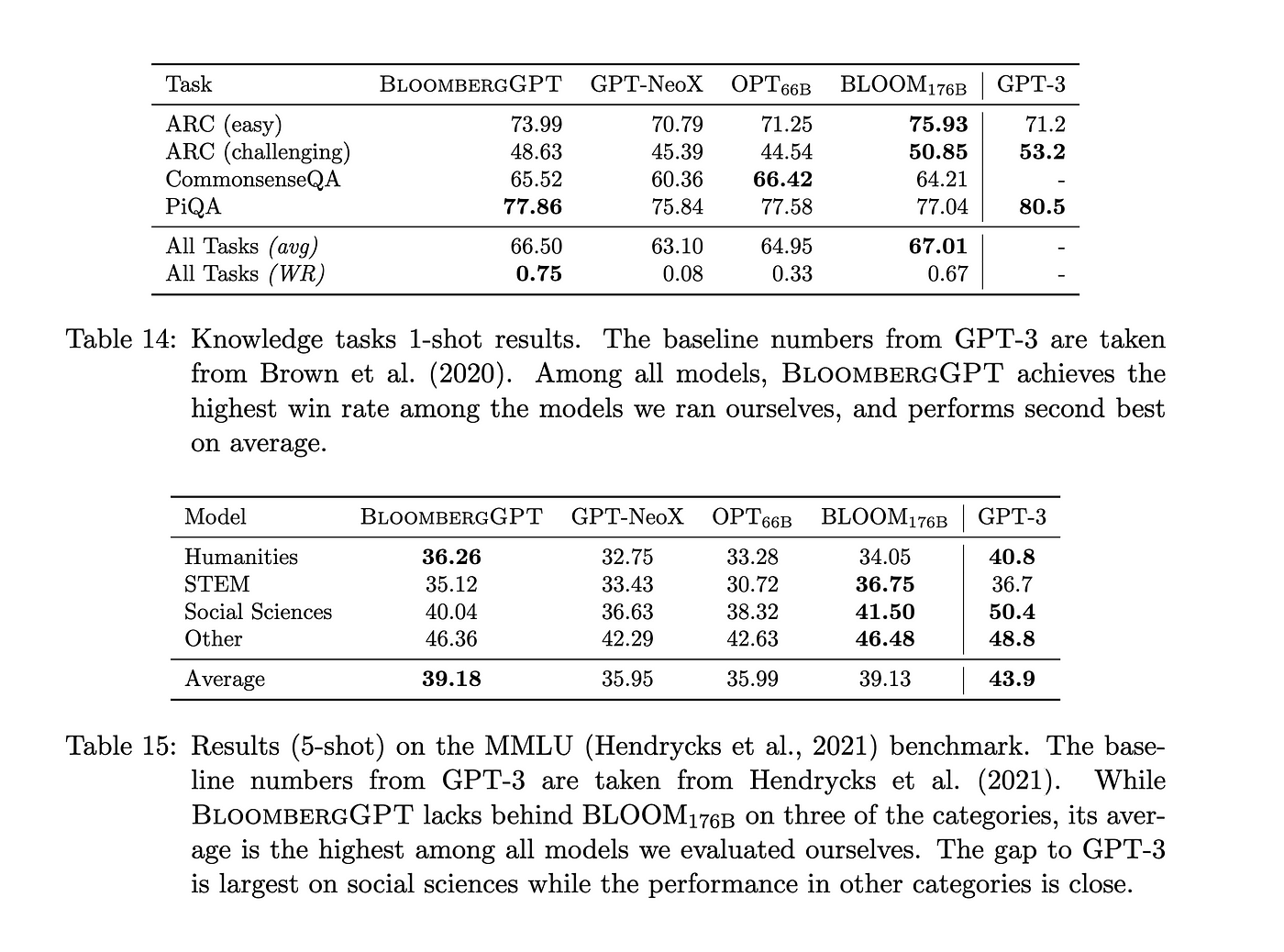
BloombergGPT: 首个金融垂直领域大语言模型

BloombergGPT: 首个金融垂直领域大语言模型

BloombergGPT: 首个金融垂直领域大语言模型 Bloomberg 刚刚发布了一篇研究论文&#xff0c;详细介绍了他们最新的突破性技术 BloombergGPT。BloombergGPT是一个大型生成式人工智能模型&#xff0c;专门使用大量金融数据进行了训练&#xff0c;以支持金融行业自然语言处理 (NLP…
阅读更多...
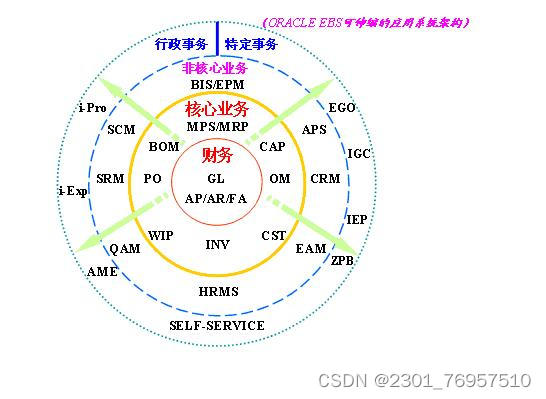
ORACLE EBS 系统架构与应用实践（一）

ORACLE EBS 系统架构与应用实践（一）

一、从ERP到EBS 从上世纪70年代晚期的物料需求计划MRP&#xff08;Material Requirements Planning&#xff09;到80年代的MRP II&#xff0c;再到90年代的企业资源计划ERP&#xff08;Enterprise Resource Planning&#xff09;&#xff0c;企业管理软件&#xff08;或曰应用…
阅读更多...
直播｜StarRocks 3.0 极速统一的湖仓新范式

直播｜StarRocks 3.0 极速统一的湖仓新范式

近期&#xff0c;StarRocks V3.0 RC 版本发布。自此&#xff0c;StarRocks 开启了从 OLAP 到 Lakehouse 演进的新篇章。 全新升级的 StarRocks 3.0&#xff1a; 通过存算分离架构&#xff0c;帮助用户降低存储成本、提升计算弹性 通过数据湖分析、物化视图等特性简化湖仓融合…
阅读更多...
从“高内聚，低耦合”说起

从“高内聚，低耦合”说起

从“高内聚&#xff0c;低耦合”说起 记得在上学的时候&#xff0c;⽼师就说过“⾼内聚&#xff0c;低耦合”&#xff0c;但当初对这句话的理解⽐较浅显。⼯作之后&#xff0c;为了说服别⼈采⽤⾃⼰设计的⽅案&#xff0c;常常说“……这样就做到了⾼内聚&#xff0c;低耦合……
阅读更多...
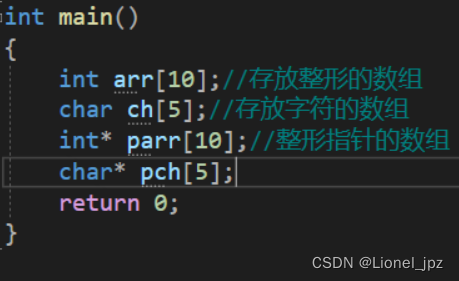
【C语言 - 初阶指针 概念、类型、野指针、指针运算】

【C语言 - 初阶指针 概念、类型、野指针、指针运算】

C语言 - 初阶指针一 指针概念注意&#xff1a;指针变量的大小&#xff1a;&#xff08;与指向的数据类型无关&#xff09;二 指针类型2.1指针类型的含义&#xff1a;2.1.1 不同指针类型决定解引用时候权限不同&#xff1a;总结&#xff1a;2.1.2 任何类型的指针变量都能存放地址…
阅读更多...
10 个高级 Python 面试问题

10 个高级 Python 面试问题

随着 Python 最近变得越来越流行&#xff0c;你们中的许多人可能正在接受与 Python 打交道的技术面试。在这篇文章中&#xff0c;我将列出十个高级 Python 面试问题和答案。 这些内容可能会令人困惑&#xff0c;并且针对的是中级开发人员&#xff0c;他们需要对 Python 作为一…
阅读更多...
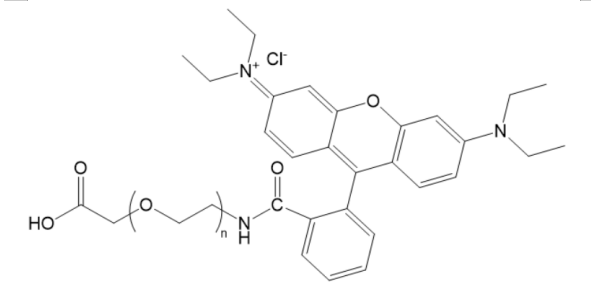
RB-PEG-COOH，罗丹明聚乙二醇羧基化学试剂简介；RhodamineB-PEG-acid

RB-PEG-COOH，罗丹明聚乙二醇羧基化学试剂简介；RhodamineB-PEG-acid

RB-PG-COOH, 罗丹明聚乙二醇羧基 中文名称&#xff1a;罗丹明-聚乙二醇-羧基 英文名称&#xff1a;RhodamineB-PEG-acid RB-PEG-COOH 性状&#xff1a;固体或粘性液体&#xff0c;取决于分子量 溶剂&#xff1a;溶于水和DCM、DMF、DMSO等常规性有机溶剂 分子量&#xff1…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023