快速排序是影响二十世纪最伟大的排序算法之一。
JDK的双轴快速排序就是对快排的优化,本质还是快排。
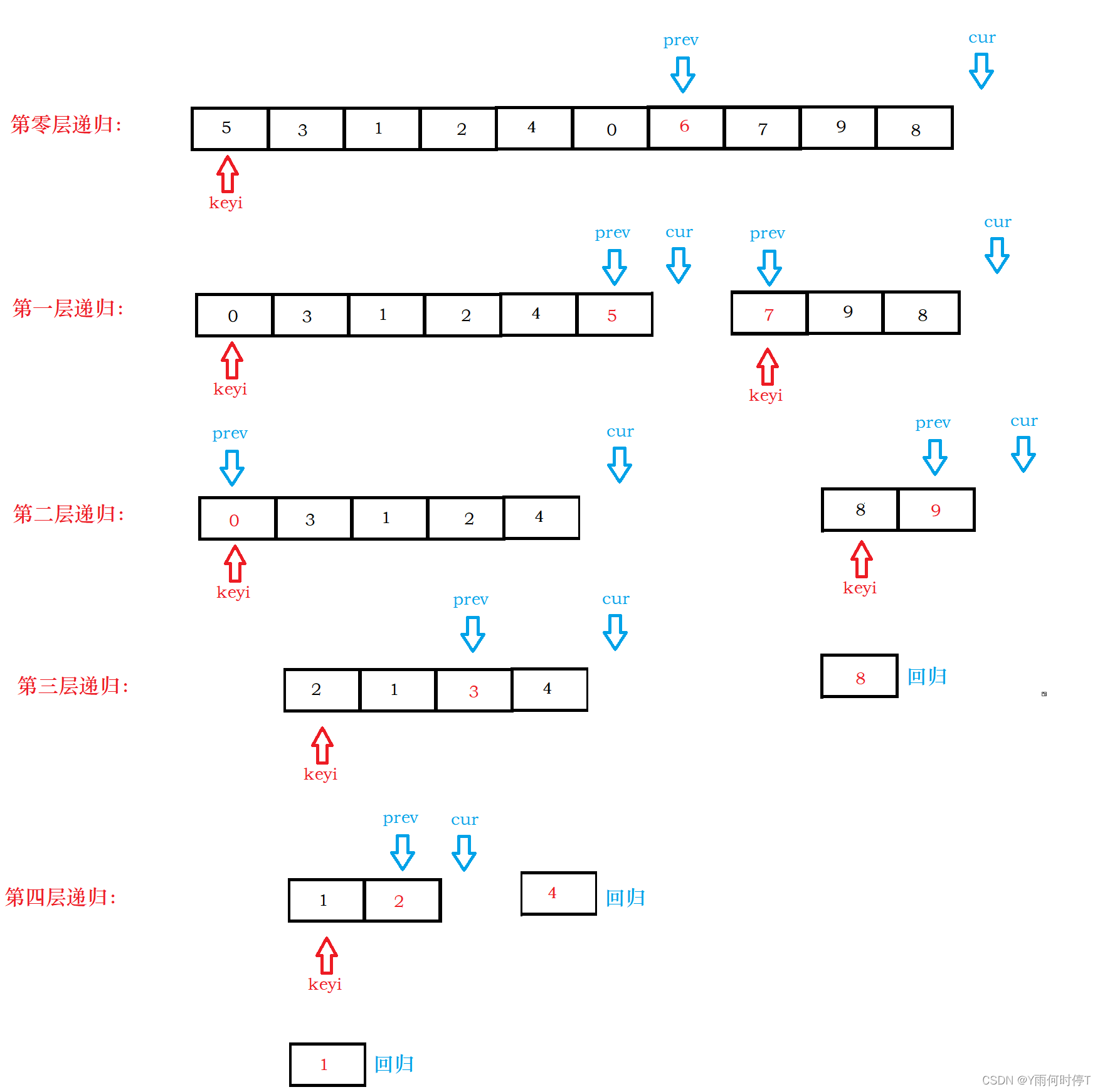
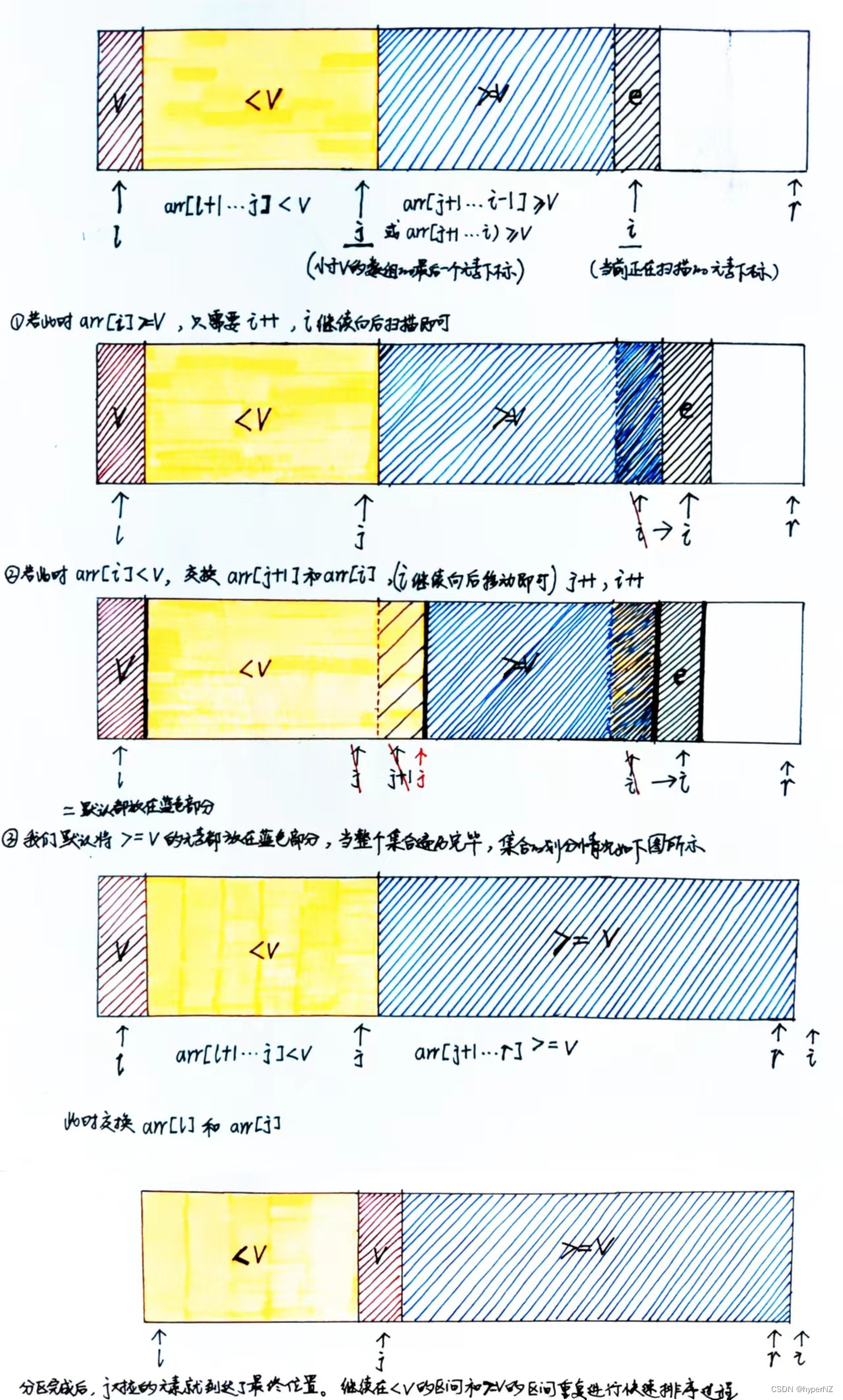
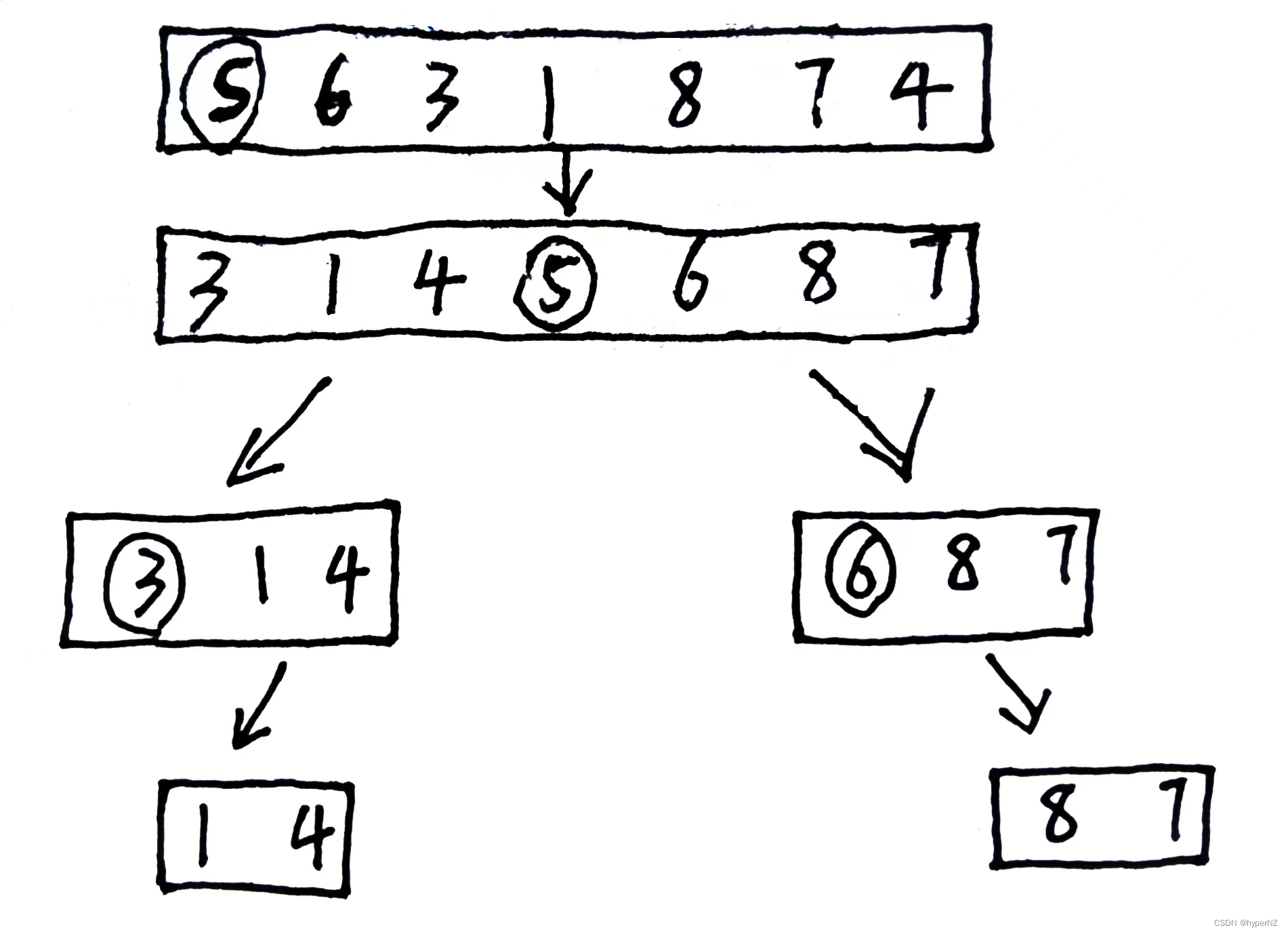
- 从待排序区间选择一个数,作为基准值/分区点(pivot),此时默认选择数组的第一个元素作为比较的基准值。
- partition:遍历整个待排序区间,将比基准值小的(可以包含相等的)放到基准值的左边,将比基准值大的(可以包含相等)放到基准值的右边。即选取一个分区点,将数组分成三部分:基准值之前的数组<基准值<基准值之后的数组。
- 采用分治思想,对左右两个小区间按照同样的方式处理,直到小区间的长度==1,代表已经有序,或者小区间长度==0,代表没有数据。
/**
* 快速排序 一路快排
* @param arr
*/
public static void quickSort(int[] arr) {
quickSortInternal(arr, 0, arr.length - 1);
}
/**
* 在l...r上进行快速排序
* @param arr
* @param l
* @param r
*/
private static void quickSortInternal(int[] arr, int l, int r) {
//递归终止时,小数组使用插入排序
if(r - l <= 15) {
insertBase(arr, l ,r);
return;
}
//选择基准值,找到该值对应的下标
int p = partition(arr, l, r);
//在<基准值区间进行快速排序
quickSortInternal(arr, l, p - 1);
//在>=基准值区间进行快速排序
quickSortInternal(arr, p + 1, r);
}
/**
* 在arr[l...r]上选择基准值,将数组划分为 <v 和 >= v 两部分,返回基准值对应的元素下标
* @param arr
* @param l
* @param r
* @return
*/
private static int partition(int[] arr, int l, int r) {
//默认选择数组的第一个元素作为基准值
int v = arr[l];
//arr[l + 1...j] < v
int j = l;
//i是当前处理的元素下标
//arr[l + 1...j] < v 最开始为空区间 [l + 1...l] = 0
//arr[j + 1...i] >= v 最开始为空区间 [l + 1...l + 1] = 0
for (int i = l + 1; i <= r; i++) {
if(arr[i] < v) {
swap(arr, j + 1, i);
//小于v的元素值新增一个
j++;
}
}
//此时j下标对应的就是最后一个 < v 的元素,交换j和l的值,选取的基准值交换到j的位置
swap(arr, l, j);
return j;
}代码在电脑上若出现问题,可能是栈溢出,解决:设置当前栈的大小为1M大小(用于50w数据)。
Environment Variables:-Xss = 1M
稳定性:不稳定。
分区时,当扫描arr[i] < v时,交换了arr[j] 和arr[i],对于arr[j + 1] >= v,就有可能把一个 = v从前面交换到了后面,分区函数无法保证稳定性。
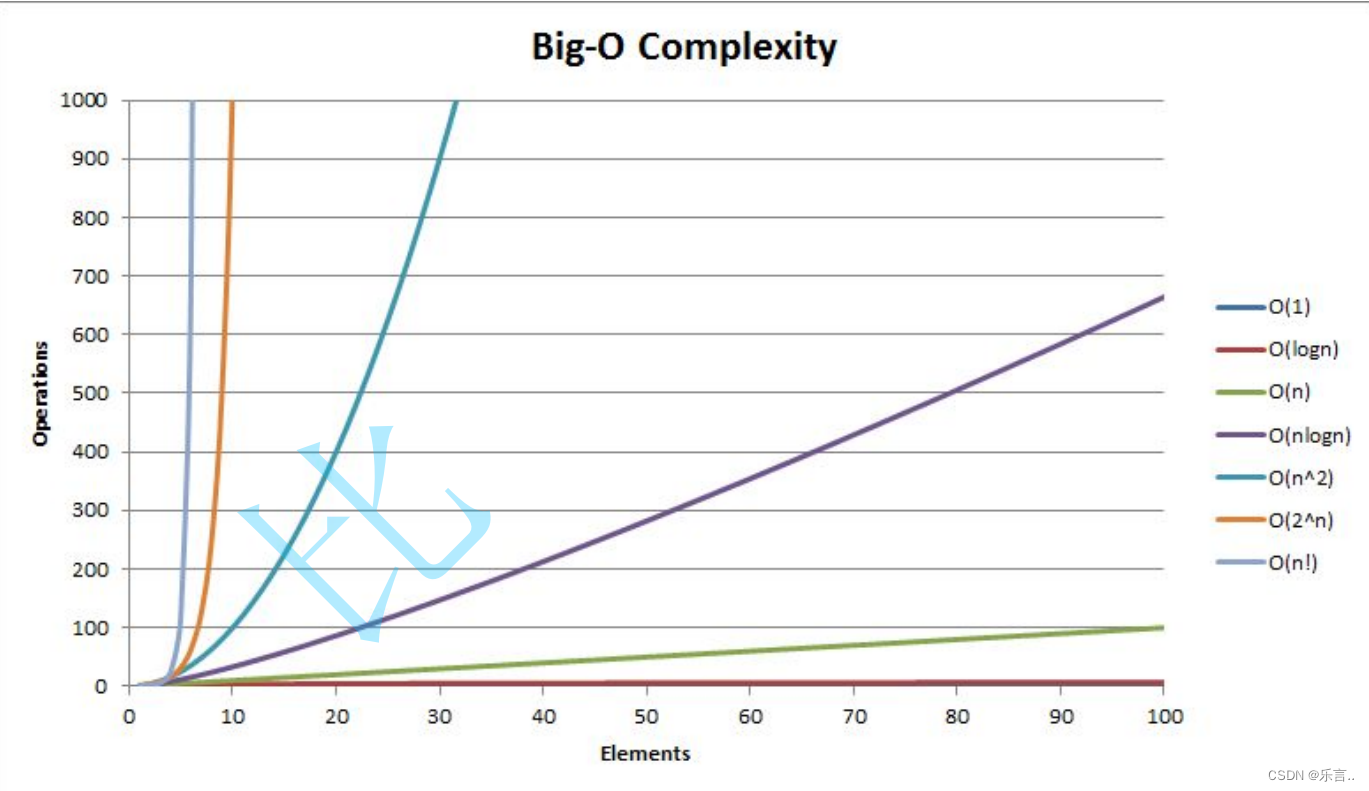
时间复杂度:O(nlogn)递归过程中调用分区函数。
- 分区函数的时间复杂度是O(n)
- 递归过程就是不断将原数组根据基准值拆分为子数组,有点类似归并拆分。递归次数就是递归树的高度,时间复杂度是O(logn)
①当待排序元素接近有序时,递归树会退化为单支树(链表),快速排序的性能衰减为O(n ^ 2)。

解决->随机化快排:在数组中随机选取一个元素作为基准值,平衡左右两个子树的元素个数。
private static final ThreadLocalRandom random = ThreadLocalRandom.current();
/**
* 快速排序 一路快排
* @param arr
*/
public static void quickSort(int[] arr) {
quickSortInternal(arr, 0, arr.length - 1);
}
/**
* 在l...r上进行快速排序
* @param arr
* @param l
* @param r
*/
private static void quickSortInternal(int[] arr, int l, int r) {
//递归终止时,小数组使用插入排序
if(r - l <= 15) {
insertBase(arr, l ,r);
return;
}
//选择基准值,找到该值对应的下标
int p = partition(arr, l, r);
//在<基准值区间进行快速排序
quickSortInternal(arr, l, p - 1);
//在>=基准值区间进行快速排序
quickSortInternal(arr, p + 1, r);
}
/**
* 在arr[l...r]上选择基准值,将数组划分为 <v 和 >= v 两部分,返回基准值对应的元素下标
* @param arr
* @param l
* @param r
* @return
*/
private static int partition(int[] arr, int l, int r) {
//优化:随机选择一个元素值作为基准值(在当前数组中)
int randomIndex = random.nextInt(l, r);
swap(arr, l, randomIndex);
int v = arr[l];
//arr[l + 1...j] < v
int j = l;
//i是当前处理的元素下标
//arr[l + 1...j] < v 最开始为空区间 [l + 1...l] = 0
//arr[j + 1...i] >= v 最开始为空区间 [l + 1...l + 1] = 0
for (int i = l + 1; i <= r; i++) {
if(arr[i] < v) {
swap(arr, j + 1, i);
//小于v的元素值新增一个
j++;
}
}
//此时j下标对应的就是最后一个 < v 的元素,交换j和l的值,选取的基准值交换到j的位置
swap(arr, l, j);
return j;
}②当集合中包含大量重复元素时,最坏的情况是:集合中全是相等的元素。按照我们的分区,一个分区没有元素,一个分区元素为n,快排性能再次衰减为O(n ^ 2)。
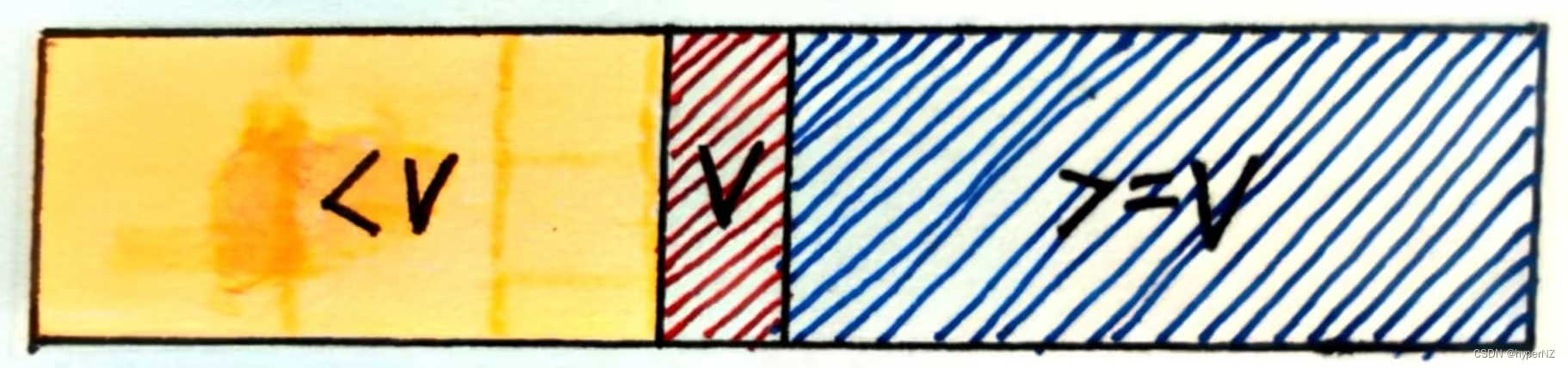
导致蓝色区域元素个数远远大于橙色区域的元素个数,造成递归树的严重倾斜。
解决->二路快排/三路快排:将相等的元素均匀分布在左右两个子区间,保证递归树的平衡性。