加粗样式通俗理解:你会注意什么?
对于一个模型而言(CNN,LSTM),模型本身很难决定什么重要什么不重要,因此注意力机制诞生了。
注意力机制:我们会把焦点聚焦在比较重要的事务上
怎么做注意力
对象:我(查询对象Q),这张图(被查询对象V)
面对一张图,人会判断哪些东西重要哪些东西不重要(计算Q和V中事物的重要度=相似度计算=Q和V中哪些东西更接近)
如何计算Q和K的相似度?→用点乘的方式,点乘其实就是内积cos
Q是查询对象, K = K 1 , K 2 , ⋯ , K n K=K_1,K_2,\cdots,K_n K=K1,K2,⋯,Kn是要查询的事物key
通过点乘的方法计算Q和K里的每一个事物的相似度,就可以拿到Q和 k 1 k_1 k1的相似值 s 1 s_1 s1,Q和 k 2 k_2 k2的相似值 s 2 s_2 s2,Q和 k n k_n kn的相似值 s n s_n sn
做一层 s o f t m a x ( s 1 , s 2 , ⋯ , s n ) softmax(s_1,s_2,\cdots,s_n) softmax(s1,s2,⋯,sn)就可以得到概率 ( a 1 , a 2 , ⋯ , a n ) (a_1,a_2,\cdots,a_n) (a1,a2,⋯,an)
因此就可以找到哪个对Q而言更重要

在上图中,Query表示查询对象,Key表示被查询对象,F(Q,K)表示Q和K进行内积,得到相似度值s,然后做softmax归一化,得到四个概率
a
1
a_1
a1,
a
2
a_2
a2,
a
3
a_3
a3,
a
4
a_4
a4。
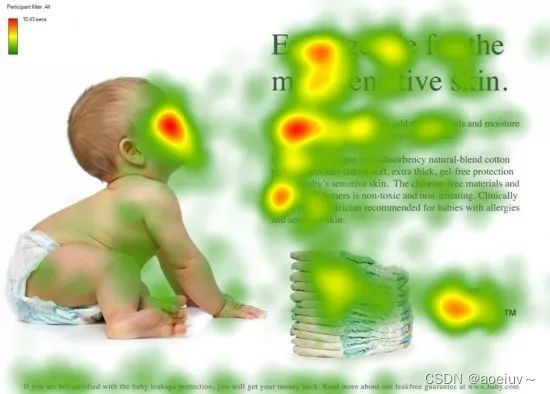
还要进行汇总,当使用Q查询结束后,Q已经失去了它的使用价值(在阶段3失去了使用价值),最终还是要拿到该图片的,只不过这张图片多了一些信息(多了一些对于我而言什么信息更重要,什么信息不重要),如下发的热力图,在红色部分是重要的信息。
怎么注意这些重要的部分?
(
a
1
,
a
2
,
⋯
,
a
n
)
∗
(
v
1
,
v
2
,
⋯
,
v
n
)
=
(
a
1
∗
v
1
,
a
2
∗
v
2
,
⋯
,
a
n
∗
v
n
)
=
(
a
1
∗
v
1
+
a
2
∗
v
2
+
⋯
+
a
n
∗
v
n
)
(a_1,a_2,\cdots,a_n)*(v_1,v_2,\cdots,v_n)=(a_1*v_1,a_2*v_2,\cdots,a_n*v_n)=(a_1*v_1+a_2*v_2+\cdots+a_n*v_n)
(a1,a2,⋯,an)∗(v1,v2,⋯,vn)=(a1∗v1,a2∗v2,⋯,an∗vn)=(a1∗v1+a2∗v2+⋯+an∗vn)=V’得到一个新的V’,新的V中包含了哪些更重要,哪些不重要的信息在里面。
以前的V=
(
v
1
,
v
2
,
⋯
,
v
n
)
(v_1,v_2,\cdots,v_n)
(v1,v2,⋯,vn)
新的V’=
(
a
1
∗
v
1
,
a
2
∗
v
2
,
⋯
,
a
n
∗
v
n
)
(a_1*v_1,a_2*v_2,\cdots,a_n*v_n)
(a1∗v1,a2∗v2,⋯,an∗vn)
然后用V’代替V
一般K=V,在transformer里。K!=V也是可以的,但是K和V一定存在某种联系,这样Q和K点乘才能指导V哪些重要,哪些不重要。
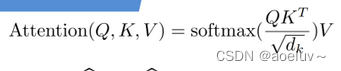
为什么在Attention公式中有一个除
d
k
\sqrt{d_k}
dk
因为经过softmax得到的概率,如果输入之间的差额越大,得到的概率越离谱
如输入是51,49,得到的概率可能是0.51,0.49
如果输入是80,20,得到的概率可能是0.99999999,0.00000001
现在多一个除
d
k
\sqrt{d_k}
dk,就可以把差额缩小
笔记来源于视频https://www.bilibili.com/video/BV1QW4y167iq/?spm_id_from=333.337.search-card.all.click&vd_source=4f67898e2b4507b9469b30d33789bb78