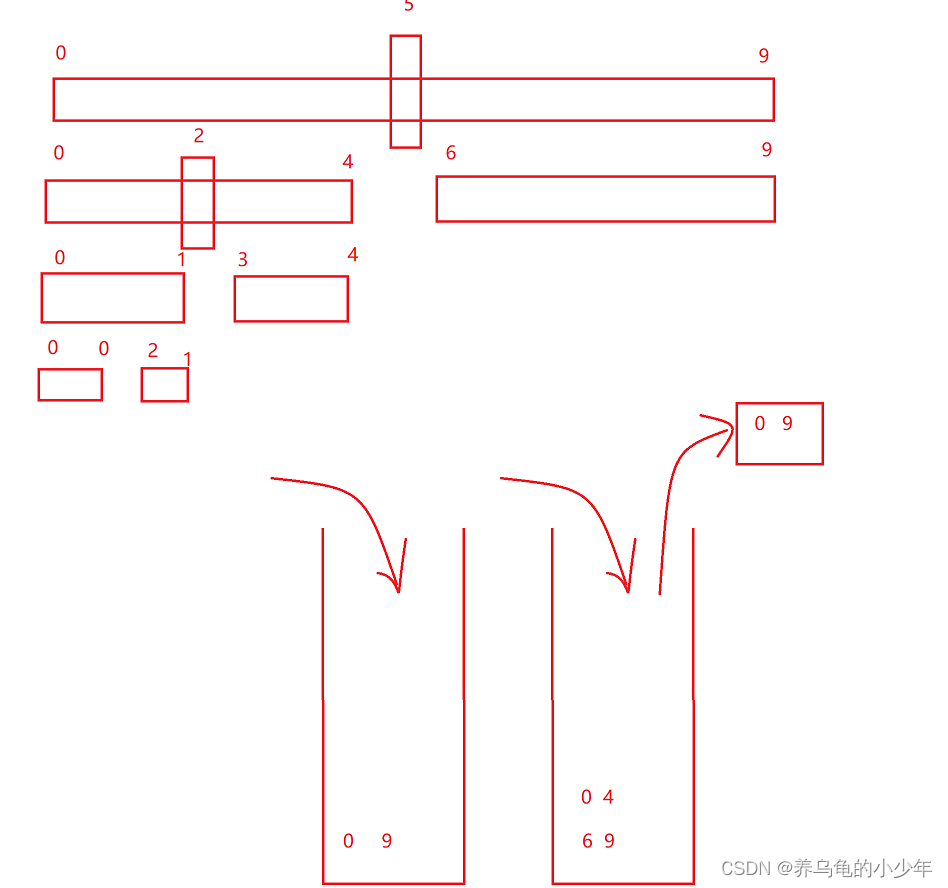
addCount 统计元素个数
private transient volatile long baseCount;
//初始化大小为2,如果竞争激烈,会扩容 2->4
private transient volatile CounterCell[] counterCells;
- 如果竞争不激烈的情况下，直接用cas (baseCount+1)
- 如果竞争激烈的情况下，采用数组的方式来进行计数。
原理如下图:
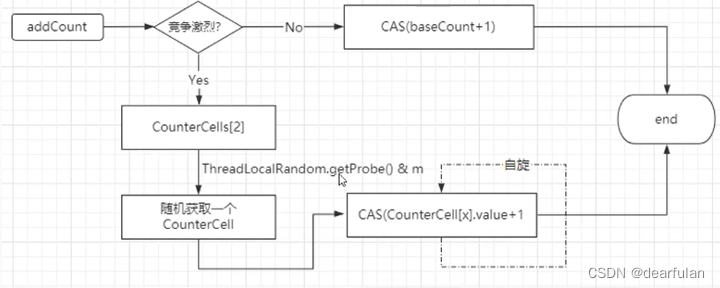
private final void addCount(long x, int check) {
CounterCell[] as; long b, s;
//统计元素个数。
if ((as = counterCells) != null ||
//CAS修改baseCount,失败则执行下述代码
!U.compareAndSwapLong(this, BASECOUNT, b = baseCount, s = b + x)) {
CounterCell a; long v; int m;
boolean uncontended = true;
if (as == null || (m = as.length - 1) < 0 ||
(a = as[ThreadLocalRandom.getProbe() & m]) == null ||
//a为获取的CounterCell里的随机一个位置的元素,尝试通过CAS更新size
!(uncontended =
U.compareAndSwapLong(a, CELLVALUE, v = a.value, v + x))) {
//完成CounterCell的初始化以及元素的累加，前面已经执行过两次CAS，执行到这里说明竞争很激烈(有很多线程操作这个map)
fullAddCount(x, uncontended);
return;
}
if (check <= 1)
return;
s = sumCount();
}
//是否要做扩容
if (check >= 0) {
Node<K,V>[] tab, nt; int n, sc;
//扩容
while (s >= (long)(sc = sizeCtl) && (tab = table) != null &&
(n = tab.length) < MAXIMUM_CAPACITY) {
int rs = resizeStamp(n);
if (sc < 0) {
if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 ||
sc == rs + MAX_RESIZERS || (nt = nextTable) == null ||
transferIndex <= 0)
break;
if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1))
transfer(tab, nt);
}
else if (U.compareAndSwapInt(this, SIZECTL, sc,
(rs << RESIZE_STAMP_SHIFT) + 2))
transfer(tab, null);
s = sumCount();
}
}
}
private final void fullAddCount(long x, boolean wasUncontended) {
int h;
if ((h = ThreadLocalRandom.getProbe()) == 0) {
ThreadLocalRandom.localInit(); // force initialization
h = ThreadLocalRandom.getProbe();
wasUncontended = true;
}
boolean collide = false; // True if last slot nonempty
//自旋
for (;;) {
CounterCell[] as; CounterCell a; int n; long v;
//counterCells已初始化
if ((as = counterCells) != null && (n = as.length) > 0) {
//如果当前位置CounterCell==null,则进行初始化
if ((a = as[(n - 1) & h]) == null) {
if (cellsBusy == 0) { // Try to attach new Cell
CounterCell r = new CounterCell(x); // Optimistic create
if (cellsBusy == 0 &&
U.compareAndSwapInt(this, CELLSBUSY, 0, 1)) {
boolean created = false;
try { // Recheck under lock
//针对已经初始化的数组的某个位置，去添加一个CounterCell。
CounterCell[] rs; int m, j;
if ((rs = counterCells) != null &&
(m = rs.length) > 0 &&
rs[j = (m - 1) & h] == null) {
rs[j] = r;
created = true;
}
} finally {
cellsBusy = 0;
}
if (created)
break;
continue; // Slot is now non-empty
}
}
collide = false;
}
else if (!wasUncontended) // CAS already known to fail
wasUncontended = true; // Continue after rehash
else if (U.compareAndSwapLong(a, CELLVALUE, v = a.value, v + x))
break;
else if (counterCells != as || n >= NCPU)
collide = false; // At max size or stale
else if (!collide)
collide = true;
//扩容部分.
else if (cellsBusy == 0 &&
U.compareAndSwapInt(this, CELLSBUSY, 0, 1)) { //获得锁
try {
if (counterCells == as) {// Expand table unless stale
CounterCell[] rs = new CounterCell[n << 1]; //扩容一倍
//迁移旧数据，遍历数组，添加到新的数组中。
for (int i = 0; i < n; ++i)
rs[i] = as[i];
counterCells = rs;
}
} finally {
cellsBusy = 0;
}
collide = false;
continue; // Retry with expanded table
}
h = ThreadLocalRandom.advanceProbe(h);
}
//第一次进入的时候会走到这个分支,如果CounterCell为空, 初始化CounterCell，需要保证在初始化过程的线程安全性。
else if (cellsBusy == 0 && counterCells == as &&
U.compareAndSwapInt(this, CELLSBUSY, 0, 1)) { //cas成功，说明当前线程抢到了锁。
boolean init = false;
try { // Initialize table
if (counterCells == as) {
//初始化长度为2的数组，
CounterCell[] rs = new CounterCell[2];
rs[h & 1] = new CounterCell(x); //把x保存到某个位置.
counterCells = rs; //复制给成员变量counterCells
init = true;
}
} finally {
cellsBusy = 0; //释放锁.
}
if (init)
break;
}
//如果前面的操作都失败，那么最后直接尝试通过CAS修改baseCount。
else if (U.compareAndSwapLong(this, BASECOUNT, v = baseCount, v + x))
break; // Fall back on using base
}
}
注意:CHM在获取当前size的时候并没有加锁,所以并不是线程安全的，如果其他线程在执行put方法时,将数据插入到CHM,但是还没有执行addCount更新size数，调用size()方法获取到的并不是最新的size大小
为什么size不用线程安全的实现呢？
实现线程安全是需要加锁的，有性能开销,目前的逻辑已经可以保证最终一致性,对业务来说，一般也不太需要在并发场景下去获取CHM的精确size
public int size() {
long n = sumCount();
return ((n < 0L) ? 0 :
(n > (long)Integer.MAX_VALUE) ? Integer.MAX_VALUE :
(int)n);
}
final long sumCount() {
CounterCell[] as = counterCells; CounterCell a;
long sum = baseCount;
if (as != null) {
for (int i = 0; i < as.length; ++i) {
if ((a = as[i]) != null)
sum += a.value;
}
}
return sum;
}
CHM的红黑树
红黑树是一种特殊的平衡二叉树，平衡二叉树具备的特征是：二叉树左子树和右子树的高度差的绝对值不超过1。
为了更好的理解平衡二叉树，我们先来了解一下二叉搜索树（Binary Search Tree)，下图就是一棵符合平衡二叉搜索树特征的二叉树。
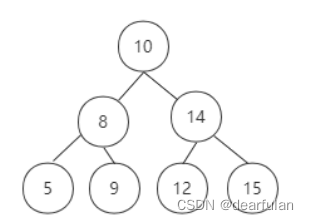
二叉搜索树从理论上来说，时间复杂度为O(logn)，但是在种极端情况下，如
果插入的元素都是符合大于根节点的值时，二叉树就变成了链表结构，这个时候对于数据的查询、插入、删除等操作，时间复杂度变成了O(n)
因此引入了平衡二叉树，平衡二叉树能够保证在极端的情况下，二叉树仍然能够保持绝对平衡，也就是左子树和右子树的高度差的绝对值不超过1。平衡二叉树为了满足绝对的平衡，在插入和删除元素的时候，只要存在不满足条件的情况，就需要通过旋转来保持平衡，而这个平衡过程比较耗时。
权衡了二叉树的平衡性以及性能，又引入了红黑树，它相当于适当放宽了平衡的要求，所以红黑树又称为特殊的平衡二叉树
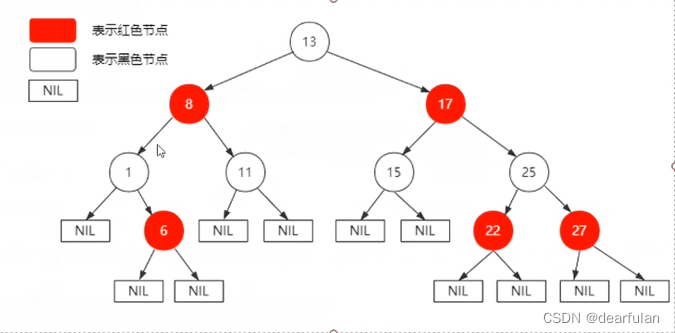
红黑树的平衡规则
- 红黑树的每个节点颜色只能是红色或者黑色。
- 根节点是黑色。
- 如果当前的节点是红色，那么它的子节点必须是黑色。
- 所有叶子节点（NIL节点，NIL节点表示叶子节点为空的节点）都是黑色。
- 从任一节点到其每个叶子节点的所有简单路径都包含相同数目的黑色节点。
下图就是一个红黑树
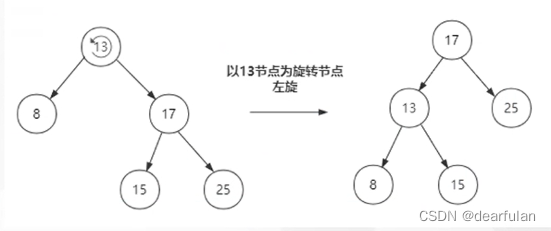
红黑树为了达到平衡，会进行左旋和右旋，如下图所示:
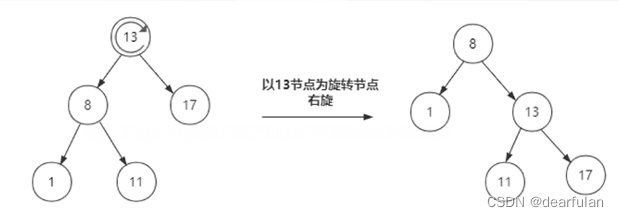所有节点在添加到红黑树的时候都是以红色节点来添加。
Why?
这是因为以红色节点来添加的话，破坏红黑树的平衡的可能性比较低(如果新加的节点的父节点是黑色的话，那么基本只要加入新节点就OK了，不需要进行旋转。)
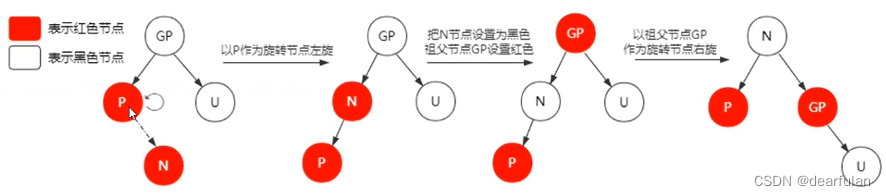
添加新节点后导致的平衡处理
- 当前是空树 没有其他变动
- 插入节点的父节点是黑色 直接插入即可
- 插入节点的父节点是红色 (说明这个节点一定不是父节点)
- 叔叔节点是红色 : 将父节点和叔叔节点都变为黑色，然后向前传递(直到根节点,根节点仍旧为黑色)
- 叔叔节点是黑色 参见下面的图片示例
- 当前新节点是左子树
- 新节点的父节点是左子节点
- 新节点的父节点是右子节点
- 当前新节点是右子树
- 新节点的父节点是左子节点
- 新节点的父节点是右子节点
- 当前新节点是左子树
tableSizeFor
tableSizeFor()方法是将任意设置的容量转换为2的n次方-1的值，将结果加一，就变成了 2 的整数幂形式。
/**
* Returns a power of two table size for the given desired capacity.
* See Hackers Delight, sec 3.2
*/
private static final int tableSizeFor(int c) {
int n = c - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
2的整数次幂的二进制形式为：2 -> 10，4 -> 100，8 -> 1000，依次类推。上面的代码就是把任意的整数转换为有效位数都是 1的二进制形式，例如 10 (二进制为 1010)，经过位运算就变成 15 -> 1111，此时把 n + 1，即 15 + 1 = 16，就得到了大于 10 的最小 2 的整数次幂的数 16。
这里先把 c 减一，是防止 c 本身就是 2 的整数次幂，经过位运算变成了原来的 2 倍。如果 c = 0，即 n = -1，经过位运算后 n 仍然是 -1。计算机使用补码存储数字，-1 的补码全是 1，所以无论怎么移位，与 -1 取或运算，其值仍是 -1。
证明：
假设存在一个正整数 n，其二进制形式为xxxx xxx1x xxxx xxxx，因为正整数的二进制形式至少存在一个 1。当执行n |= n >>> 1后，n 的二进制形式就变成 xxxx xx11 xxxx xxxx，因为 1 与任何位取或都是 1。就相当于在原来 1 的右边增加了一个 1。执行n |= n >>> 2后，n 的二进制形式变成xxxx xx11 11xx xxxx，依次类推，执行完所有的或运算后，n 的最高位的 1 右边的位全部变成 1
get源码分析
public V get(Object key) {
Node<K,V>[] tab; Node<K,V> e, p; int n, eh; K ek;
// 计算哈希值
int h = spread(key.hashCode());
// 判断tab是否已初始化，key计算后的hash值对应的位置是否有元素
if ((tab = table) != null && (n = tab.length) > 0 &&
(e = tabAt(tab, (n - 1) & h)) != null) {
// 该位置有元素,则判断链表头节点是否就是要找的节点
if ((eh = e.hash) == h) {
if ((ek = e.key) == key || (ek != null && key.equals(ek)))
return e.val;
}
//en<0表示此时处于扩容中,该节点已迁移到新table
else if (eh < 0)
return (p = e.find(h, key)) != null ? p.val : null;
// 如果链表的头节点不是要找的节点,则向下寻找
while ((e = e.next) != null) {
if (e.hash == h &&
((ek = e.key) == key || (ek != null && key.equals(ek))))
return e.val;
}
}
// 没找到相同key的节点
return null;
}
//这个操作是将 hash 值的低 16 位进行了第二次哈希计算，将低 16 位的值打散
static final int spread(int h) {
// 将hash值的低16位与高16位进行异或计算，而高16位保持不变。
// HASH_BITS=0x7fffffff，将hash值的符号位 置为0，其它位不变，确保hash值非负。
return (h ^ (h >>> 16)) & HASH_BITS;
}
CHM中计算下标的方式是(n - 1) & h，n 为 2 的整数幂，所以 n - 1的二进制形式为00…011…11，(n - 1) & h 其实就是将 hash 值的低若干位取出来作为位置下标，这就要求 hash 低位值要比较分散，这样才能尽可能的减少 hash 冲突
ConcurrentHashMap总结
- 保证线程安全 (保证添加元素的线程安全,但是不保证size()一定获取到最新的数据,最终是一致的)
- 实现原理
- put方法添加元素，创建数据
- 发生hash冲突 -> 链表，链式寻址
- 分段锁 仅在发生hash冲突的节点上加锁，锁的范围限制在单个节点上
- 扩容 -> 数组的扩容 ->
- 数据迁移
- 多线程并发协助数据迁移
- 高低位迁移: 把需要迁移的数据放在高位链，不需要迁移的放在低位链， 然后一次性把高位和地位链set到指定的新数组的下标位置。
- 元素的统计
- 使用数组，每个数组记录一部分size， 分片的设计思想。
- size, 数组之和+baseCount的值来完成数据累加
- 当链表长度大于等于8，并且数组长度大于64的时候，链表转化为红黑树
