1. 题目介绍（51. 数组中的逆序对）

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

在这里插入图片描述

【测试用例】：
示例 1:

输入: [7,5,6,4]
输出: 5

【条件约束】：

限制：

0 <= 数组长度 <= 50000

2. 题解

2.1 枚举 – O(n²)

时间复杂度O(n²)，空间复杂度O(1)

【解题思路】：
该题最直接的思路就是 枚举。顺序扫描整个数组，每扫描到一个数字，逐个比较该数字和它后面的数字的大小。如果后面的数字比它小，则这两个数字就组成一个逆序对。假设数组中含有 n 个数字。由于每个数字都要和 O(n) 个数字进行比较，因此这种算法的时间复杂度是 O(n²)。
……
【实现策略】：

定义变量 n，用来记录输入数组长度，然后以此进行无效输入判断；
定义变量 count，用来记录这个数组中逆序对的总数;
实现双重循环，让每个数字都与其后面的所有数字进行比较；
循环结束，返回 count.

class Solution {
    // Soultion1：枚举
    public int reversePairs(int[] nums) {
        // 定义变量 n，用来记录输入数组长度
        int n = nums.length;
        // 无效输入判断
        if (n <= 1) return 0;
        // 定义变量 count，用来记录这个数组中逆序对的总数
        int count = 0;
        // 双重循环，让每个数字都与其后面的所有数字进行比较
        for (int i = 0; i < n; i++) {
            for (int j = i+1; j < n; j++) {
                if (nums[i] > nums[j]) count++;
            }
        }
        // 循环结束，返回结果
        return count;
    }
}

在这里插入图片描述

2.2 归并排序 – O(nlogn)

时间复杂度O(nlogn)，空间复杂度O(n)

【解题思路】：
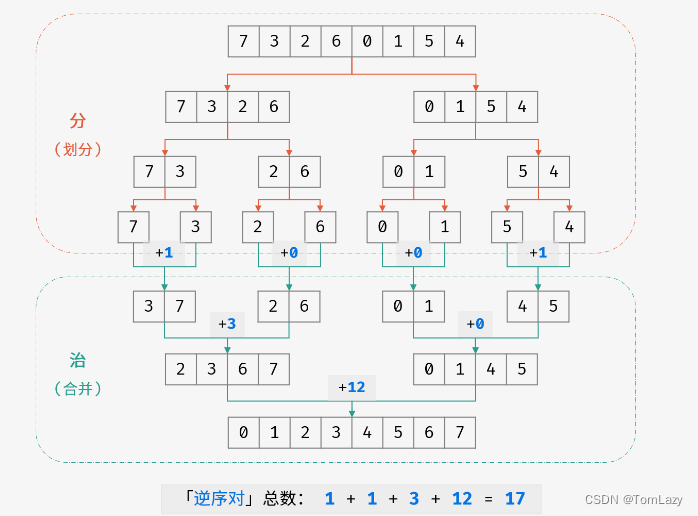
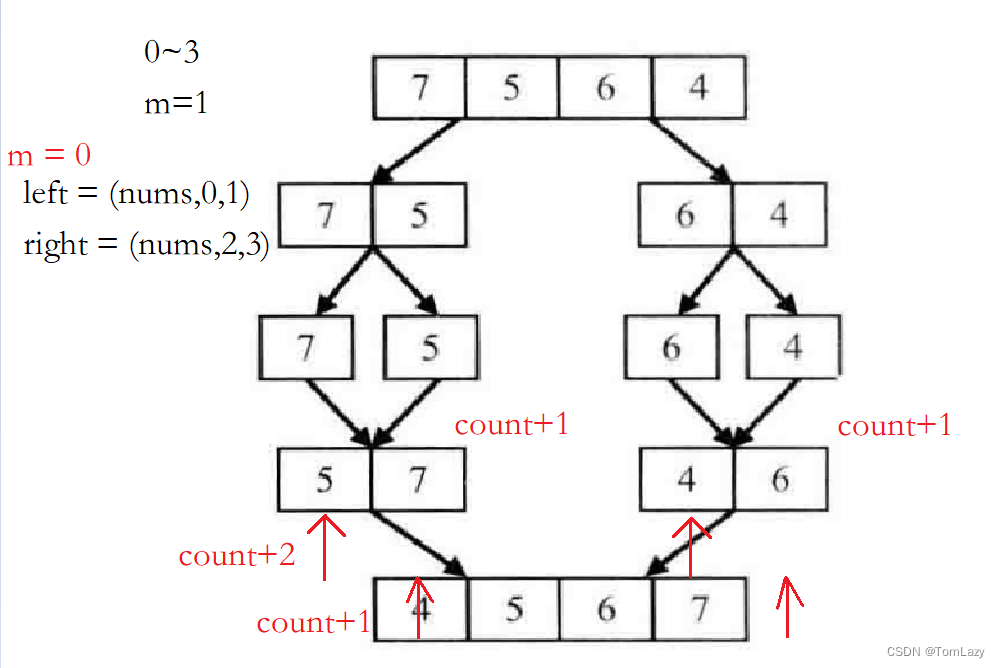
以数组 {7，5，6，4} 为例来分析统计逆序对的过程。每扫描到一个数字的时候，我们不能拿它和后面的每一个数字进行比较，否则时间复杂度就是
O(n²)，因此我们可以 考虑先比较两个相邻的数字。
……
依据这种思想，我们可以将数组进行以下四步的操作，即：

拆分
合并
统计
排序

其中合并和统计可以一块进行。
……
而这个排序的过程实际上就是 归并排序，归并排序可参考：【算法】排序算法之归并排序
……
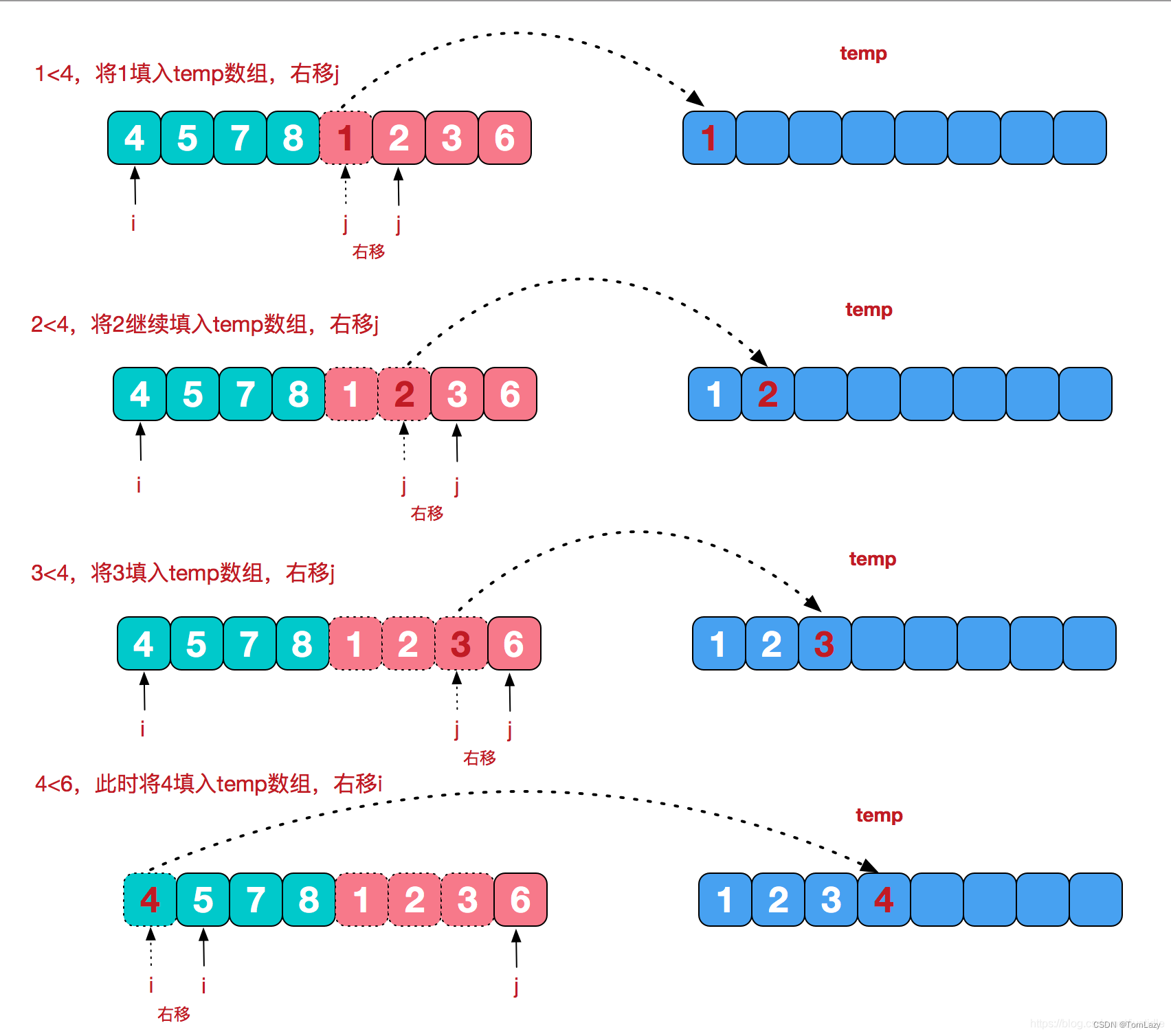
合并过程可参考：

合并阶段本质上是 合并两个排序数组 的过程，而每当遇到 左子数组当前元素 > 右子数组当前元素 时，意味着「左子数组当前元素至末尾元素」与「右子数组当前元素」构成了若干「逆序对」，同时，我们要将较小的那个元素存入临时数组中

……
【实现策略】：

利用数组长度 n 进行无效输入判断；
对数组 nums 进行归并排序；
递归划分左右区域；
合并、判断、排序；

在这里插入图片描述

class Solution {
    // Soultion2：归并排序
    int[] nums;
    public int reversePairs(int[] nums) {
        // 定义变量 n，用来记录输入数组长度
        int n = nums.length;
        // 无效输入判断
        if (n <= 1) return 0;
        // 初始化数组
        this.nums = nums;
        // 定义变量 count，用来记录这个数组中逆序对的总数
        int count = mergeSort(nums,0,n-1);
        // 循环结束，返回结果
        return count;
    }

    public int mergeSort(int[] nums,int l,int r){
        // 当只有一个节点的时候，直接返回，退出递归
        if(l >= r) return 0;
        // 递归划分
        int mid = l + (r - l) / 2;
        // 左拆分
        int left = mergeSort(nums,l,mid);
        // 右拆分
        int right = mergeSort(nums,mid+1,r);
        // 合并
        int count = merge(nums,l,mid,r);
        // 返回最终结果
        return left + right + count;
    }

    public int merge(int[] nums,int left,int mid,int right){
        int count = 0;
        // 定义一个临时数组
        int[] temp = new int[right-left+1];
        // 定义一个指针，指向第一个数组的第一个元素
        int i = left;
        // 定义一个指针，指向第二个数组的第一个元素
        int j = mid+1;
        // 定义一个指针，指向临时数组的第一个元素
        int t = 0;
        // 当两个数组都有元素的时候，遍历比较每个元素大小
        while(i <= mid && j <= right){
            // 比较两个数组的元素，取较小的元素加入到，临时数组中
            // 并将两个指针指向下一个元素
            if(nums[i] <= nums[j]){
                temp[t++] = nums[i++];
            }else{
                // 当左边数组的大与右边数组的元素时，就对当前元素以及后面的元素的个数进行统计，
                // 此时这个数就是，逆序数
                // 定义一个计数器，记下每次合并中存在的逆序数。
                count += mid-i+1;
                temp[t++] = nums[j++];
            }
        }
        // 当左边的数组没有遍历完成后，直接将剩余元素加入到临时数组中
        while(i <= mid){
            temp[t++] = nums[i++];
        }
        // 当右边的数组没有遍历完成后，直接将剩余元素加入到临时数组中
        while(j <= right){
            temp[t++] =nums[j++];
        }
        // 将新数组中的元素，覆盖nums旧数组中的元素。
        // 此时数组的元素已经是有序的
        for(int k =0; k< temp.length;k++){
            nums[left+k] = temp[k];
        }
        return count;
    }
}