目录
第一题:05.替换空格
第二题:06.从尾到头打印链表
第三题:11.旋转数组的最小数字编辑
第四题:17.打印从1到最大的n位数
第五题:29.顺时针打印矩阵
第六题:53.在排序数组中查找数字
第七题:57.和为s的两个数字
第八题:57.和为s的连续正数序列
第九题:58.翻转单词顺序
第十题:58.左旋字符串
第十一题:62.圆圈中最后剩下的数字
第十二题:61.扑克牌中的顺子
第一题:05.替换空格
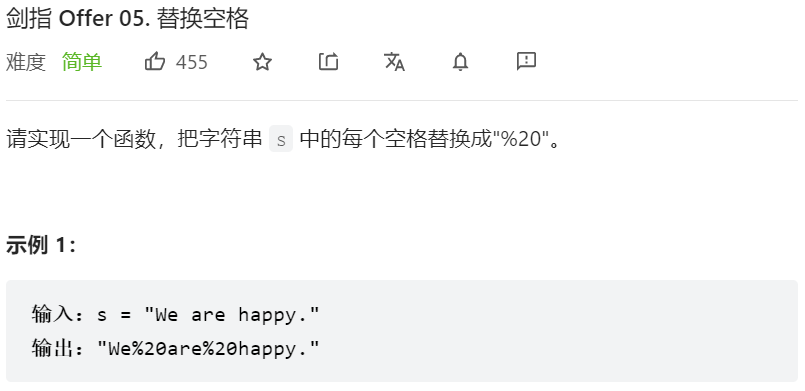
我的答案:replace方法
class Solution {
public String replaceSpace(String s) {
return s.replace(" ","%20");
}
}
官方答案:
法一:字符数组
class Solution {
public String replaceSpace(String s) {
int length = s.length();
char[] array = new char[length * 3];
int size = 0;//size表示替换后的字符串的长度
for (int i = 0; i < length; i++) {
char c = s.charAt(i);//获取s的当前字符
if (c == ' ') {
array[size++] = '%';
array[size++] = '2';
array[size++] = '0';
} else {
array[size++] = c;
}
}
String newStr = new String(array, 0, size);//把 array 的前 size 个字符转成字符串返回
return newStr;
}
}第二题:06.从尾到头打印链表
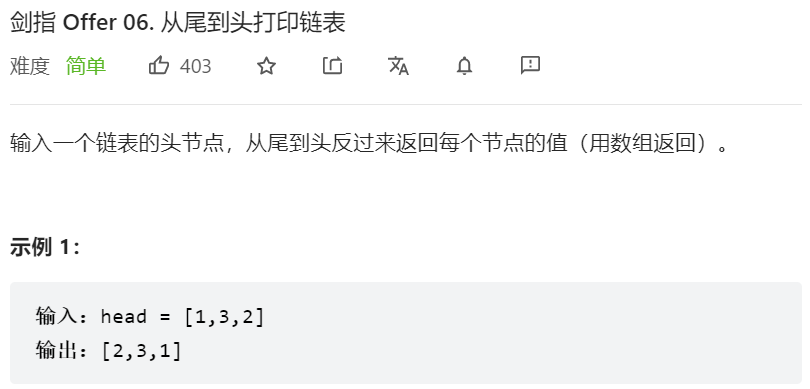
我的答案:
法一:栈
class Solution {
public int[] reversePrint(ListNode head) {
Stack<Integer> stack=new Stack<>();
int counts=0,len=0;//len是链表长度,counts是数组下标
ListNode tmp=head;
while(tmp!=null){//将链表里的数全部压入栈中,顺便得到链表的长度(用于下面创建数组)
stack.add(tmp.val);
len++;
tmp=tmp.next;
}
int[] arr=new int[len];
while(!stack.isEmpty()){//把栈里的值先进后出地存入数组中
arr[counts++]=stack.pop();
}
return arr;
}
}
法二:普通方法
class Solution {
public int[] reversePrint(ListNode head) {
int len=0;//链表长度
ListNode tmp=head;
while(tmp!=null){//
len++;
tmp=tmp.next;
}
int[] arr=new int[len];
for(int i=len-1;i>=0;i--){
arr[i]=head.val;
head=head.next;
}
return arr;
}
}
官方答案:
法一:栈
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public int[] reversePrint(ListNode head) {
Stack<ListNode> stack = new Stack<ListNode>();
ListNode temp = head;//注意这步,创建一个新指针用于遍历链表
//如果直接用head,遍历完后,head就指向链表尾部,再回头部很麻烦
while (temp != null) {
stack.push(temp);//将指针指向的节点压入栈内
temp = temp.next;//将指针移到当前节点的下一个节点
}
int size = stack.size();//获取栈的大小,用于创建数组
int[] print = new int[size];
for (int i = 0; i < size; i++) {//遍历栈,把节点的值存到数组中
print[i] = stack.pop().val;
}
return print;
}
}
网友答案:递归
class Solution {
ArrayList<Integer> tmp = new ArrayList<Integer>();
public int[] reversePrint(ListNode head) {
recur(head);//存储反转的链表
int[] res = new int[tmp.size()];
for(int i = 0; i < res.length; i++)//把列表里的值加入数组中返回
res[i] = tmp.get(i);
return res;
}
void recur(ListNode head) {
if(head == null) return;//递归到头了
recur(head.next);//递归入口
tmp.add(head.val);//将当前节点值加入列表
}
}
第三题:11.旋转数组的最小数字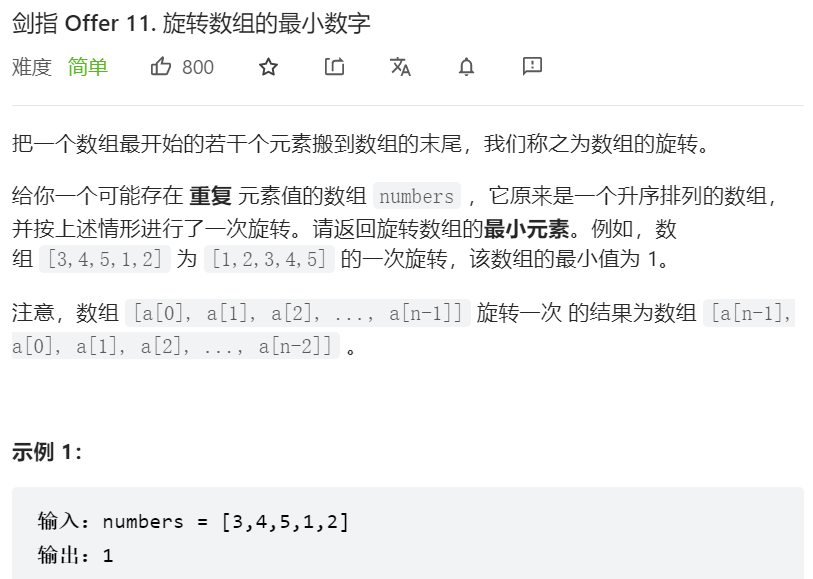
我的答案:
法一:排序函数
class Solution {
public int minArray(int[] numbers) {
Arrays.sort(numbers);
return numbers[0];
}
}
法二:普通方法
class Solution {
public int minArray(int[] numbers) {
for(int i=0;i<numbers.length-1;i++){
if(numbers[i]>numbers[i+1]){//旋转数组【2,2,2,0,1】
return numbers[i+1];
}
}
return numbers[0];//数组没有旋转,而且是长序数组,所以返回数组的第一个元素
}
}官方答案:
法一:二分查找
旋转后的数组性质:
数组中的最后一个元素 x:在最小值右侧的元素,它们的值一定都小于等于 x;而在最小值左侧的元素,它们的值一定都大于等于 x。如:[3,4,5,1,2]
class Solution {
public int minArray(int[] numbers) {
//左边界为 low,右边界为high,区间的中点为pivot
int low = 0;
int high = numbers.length - 1;
while (low < high) {
int pivot = low + (high - low) / 2;
if (numbers[pivot] < numbers[high]) {//中轴元素小于右边界值,说明中轴元素是最小值右侧的元素,此时忽略右半边数组
high = pivot;
} else if (numbers[pivot] > numbers[high]) {//中轴元素大于右边界值,说明中轴元素是最小值左侧的元素,此时忽略左半边数组
low = pivot + 1;
} else {//中轴元素等于右边界值,把右边界值删掉,同样的值留下一个即可,此时忽略十分查找区间的右端点
high -= 1;
}
}
return numbers[low];
}
}
注意:
为什么官方的二分法的题解多是写的
low + (high - low) // 2而不是(high + low) // 2?因为low+high在low和high特别大的时候可能会造成溢出,使用减法避免了溢出发生。
第四题:17.打印从1到最大的n位数
我的答案:
法一:
class Solution {
public int[] printNumbers(int n) {
int max=(int)Math.pow(10,n)-1;//10的n次方减1,在此是1000-1=999
int[] arr=new int[max];
for(int i=1,j=0;i<=max;i++){//从1遍历到999即可
arr[j++]=i;
}
return arr;
}
}
网友答案:全排列代码
class Solution {
int[] res;
int cnt = 0;
char[] num, NUM = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
void dfs(int x, int len) {//生成长度为len的数字,正在确定第 x 位
if (x == len) {
res[cnt++] = Integer.parseInt(String.valueOf(num).substring(0, len));
return ;
}
int start = x == 0 ? 1 : 0;//当 x=0 时表示左边第一位,不能为0
for (int i = start; i <= 9; ++ i) {
num[x] = NUM[i];
dfs(x + 1, len);
}
}
public int[] printNumbers(int n) {
res = new int[(int)Math.pow(10, n) - 1];
num = new char[n];
for (int i = 1; i <= n; ++ i) dfs(0, i);
return res;
}
}第五题:29.顺时针打印矩阵

我的答案:递归(运行失败)
class Solution {
int count=0;//递归次数
int counts=0;//新数组的下标
public int[] spiralOrder(int[][] matrix) {
int x=matrix[0].length;//原数组的列数
int y=matrix.length;//原数组的行数
int[] newarr=new int[x*y];
print(x,y,newarr,matrix);//递归打印数组
return newarr;
}
void print(int x,int y,int[] newarr,int[][] matrix){//打印数组的边缘一周为一次递归
for(int i=count;i<x-count;i++){
for(int j=count;j<y-count;j++){
if(i==count||i==(x-count-1)||j==count||j==(y-count-1)){
newarr[counts++]=matrix[i][j];
}
}
}
count++;
}
}官方答案:
法一:模拟
模拟打印矩阵的路径。初始位置是矩阵的左上角,初始方向是向右,当路径超出界限或者进入之前访问过的位置时,顺时针旋转,进入下一个方向。当路径的长度达到矩阵中的元素数量时即为完整路径,将该路径返回
class Solution {
public int[] spiralOrder(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {//二维数组为空,直接返回
return new int[0];
}
int rows = matrix.length, columns = matrix[0].length;//rows是原矩阵的行数,columns是原矩阵的列数
boolean[][] visited = new boolean[rows][columns];//新建二维矩阵用于存放已经访问过的数组元素,避免重复访问
int total = rows * columns;//原数组的总元素个数
int[] order = new int[total];//存放按路径访问到的元素
int row = 0, column = 0;//初始位置是矩阵的左上角,表示当前元素的坐标
int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};//用于指示下一步往哪个方向走
int directionIndex = 0;//初始方向是向右
for (int i = 0; i < total; i++) {
order[i] = matrix[row][column];
visited[row][column] = true;
int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];//表示下一个要访问的元素坐标
if (nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns || visited[nextRow][nextColumn]) {//表示走到数组的边界(分别表示上、下、左、右边界),
//或者即将访问到已经访问过的元素了,此时要变换方向
directionIndex = (directionIndex + 1) % 4;
}
row += directions[directionIndex][0];//更新变换方向后的第一个元素坐标
column += directions[directionIndex][1];
}
return order;
}
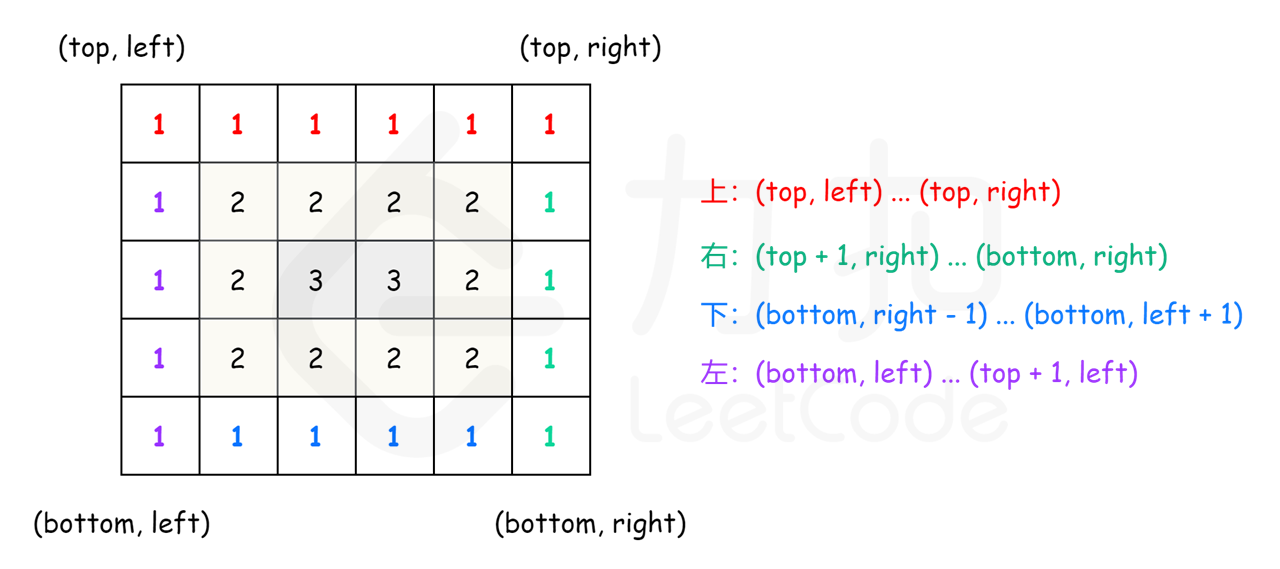
}法二:按层模拟
将矩阵看成若干层,首先打印最外层的元素,其次打印次外层的元素,直到打印最内层的元素。
class Solution {
public int[] spiralOrder(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {//二维数组为空,直接返回
return new int[0];
}
int rows = matrix.length, columns = matrix[0].length;//二维数组的行数和列数
int[] order = new int[rows * columns];//存放按路径访问的元素
int index = 0;
int left = 0, right = columns - 1, top = 0, bottom = rows - 1;//二维数组最外层的边界
while (left <= right && top <= bottom) {
for (int column = left; column <= right; column++) {//往右移
order[index++] = matrix[top][column];
}
for (int row = top + 1; row <= bottom; row++) {//往下移
order[index++] = matrix[row][right];
}
if (left < right && top < bottom) {
for (int column = right - 1; column > left; column--) {//往左移
order[index++] = matrix[bottom][column];
}
for (int row = bottom; row > top; row--) {//往上移
order[index++] = matrix[row][left];
}
}
left++;//上下左右都往里缩小一层,削掉二维数组的最外层
right--;
top++;
bottom--;
}
return order;
}
}第六题:53.在排序数组中查找数字
我的答案:
法一:普通for循环遍历
class Solution {
public int search(int[] nums, int target) {
int counts=0;//计数器
for(int i=0;i<nums.length;i++){
if(nums[i]==target)
counts++;
}
return counts;
}
}
法二:二分查找
class Solution {
public int search(int[] nums, int target) {
int lo=0,hi=nums.length-1;
int counts=0;//计数器
while(lo<=hi){
int mid=lo+(hi-lo>>1);
if(nums[mid]>target){//目标值在二分查找区间的左半部分
hi=mid-1;
}
if(nums[mid]<target){//目标值在二分查找区间的右半部分
lo=mid+1;
}
if(nums[mid]==target){//找到目标值
counts=counts+1;//这里加1,是因为中间值等于target
for(int i=mid;i<hi;){//往后找,这里不写i=mid+1,是因为怕溢出,比如数组[1],所以下面的i++放在for循环前面
i++;
if(nums[i]==target){
counts++;
}
}
for(int i=mid;i>lo;){//往前找
i--;
if(nums[i]==target){
counts++;
}
}
break;
}
}
return counts;
}
}
官方答案:
法一:二分查找
class Solution {
public int search(int[] nums, int target) {
int leftIdx = binarySearch(nums, target, true);//第一个等于target 的位置
int rightIdx = binarySearch(nums, target, false) - 1;//第一个大于target 的位置减一
if (leftIdx <= rightIdx && rightIdx < nums.length && nums[leftIdx] == target && nums[rightIdx] == target) {
return rightIdx - leftIdx + 1;//当 target 在数组中存在时,target 在数组中出现的次数为rightIdx−leftIdx+1
}
return 0;//没找到
}
public int binarySearch(int[] nums, int target, boolean lower) {
int left = 0, right = nums.length - 1, ans = nums.length;
while (left <= right) {
int mid = (left + right) / 2;
if (nums[mid] > target || (lower && nums[mid] >= target)) {
right = mid - 1;
ans = mid;
} else {
left = mid + 1;
}
}
return ans;
}
}
很经典的题,两次二分查找x,一次找到x元素最左边位置,一次找到x元素最右边的位置,最终返回的是右边的位置减左边的位置 + 1。当数组大小为零时候特殊处理,返回0。
第七题:57.和为s的两个数字
我的答案:
法一:二分查找
class Solution {
public int[] twoSum(int[] nums, int target) {
int[] arr=new int[2];//创建数组用于存储答案
for(int i=0;i<nums.length-1;i++){
int j=binarySearch(i,target,nums);//用二分查找法查找另一个元素
if(nums[i]+nums[j]==target){
arr[0]=nums[i];
arr[1]=nums[j];
return arr;
}
}
return arr;
}
public int binarySearch(int i,int target,int[] nums){
int x=i;//左边界
int y=nums.length-1;//右边界
int z=target-nums[x];//在区间[x,y]中要寻找的目标值
while(x<y){
if(nums[y]==z){//判断边界值
return y;
}
if(nums[x]==z){
return x;
}
int mid=x+(y-x>>1);//判断中间值
if(nums[mid]<z){//小了,往右边找大点
x=mid+1;
}else if(nums[mid]>z){//大了,往左边找小点
y=mid-1;
}else if(nums[mid]==z){//找到了,返回
return mid;
}
}
return 0;
}
}
法二:哈希集合
class Solution {
public int[] twoSum(int[] nums, int target) {
int[] arr=new int[2];
Map<Integer,Integer> map=new HashMap<>();
for(int i=0;i<nums.length;i++){//遍历数组,把数组里的元素都加入哈希集合
map.put(nums[i],i);//键是数组元素,值是元素下标
//数组中可能存在相同的值,但map中的键是唯一的,所以添加时,同样的值只能添加一次
}
for(int i=0;i<nums.length;i++){
int z=target-nums[i];//在map中寻找该差值
if(map.containsKey(z)){
int j=map.get(z);//获取该差值的下标
if(nums[i]+nums[j]==target){
arr[0]=nums[i];
arr[1]=nums[j];
return arr;
}
}
}
return arr;
}
}
网友答案:对撞指针
class Solution {
public int[] twoSum(int[] nums, int target) {
int i = 0, j = nums.length - 1;
while(i < j) {
int s = nums[i] + nums[j];//题目的限制条件为nums[i]小于10的六次方,不用担心相加会溢出
if(s < target) i++;//最小的加最大的都比target小,所以最小的舍弃
else if(s > target) j--;//最大的加最小的都比target大,所以最大的数舍弃
else return new int[] { nums[i], nums[j] };
}
return new int[0];
}
} 
第八题:57.和为s的连续正数序列

我的答案:普通遍历 (提交失败)
class Solution {
public int[][] findContinuousSequence(int target) {
int[][] arr=new int[target][target];
for(int i=0;i<target-1;i++){
int sum=i;
for(int j=i+1;sum<=target;j++){
sum+=j;
if(sum==target){
int x=i,count=0;
while(x<=j){
arr[i][count++]=x;
x++;
}
break;
}
}
}
return arr;
}
}输入:target = 15 应该输出:[[1,2,3,4,5],[4,5,6],[7,8]] 实际输出:[[0,1,2,3,4,5,0,0,0,0,0,0,0,0,0], [1,2,3,4,5,0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[4,5,6,0,0,0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[7,8,0,0,0,0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]]把0都输出来了,不知道咋办
官方答案:
法一:枚举+暴力
枚举每个正整数为起点,判断以它为起点的序列和 sum 是否等于 target 即可
特点在于:它创建了一个ArrayList链表,然后把一维数组当成元素灵活地存入链表中,解决了二维数组长度不能变的问题
class Solution {
public int[][] findContinuousSequence(int target) {
List<int[]> vec = new ArrayList<int[]>();//链表的元素就是一个个的一维数组
int sum = 0, limit = (target - 1) / 2; // (target - 1) / 2 等效于 target / 2 下取整
//由于题目要求序列长度至少大于2,所以枚举的上界为 ⌊target/2⌋
for (int i = 1; i <= limit; ++i) {
for (int j = i;; ++j) {
sum += j;
if (sum > target) {
sum = 0;
break;
} else if (sum == target) {
int[] res = new int[j - i + 1];//创建一维数组
for (int k = i; k <= j; ++k) {//把数组装满
res[k - i] = k;
}
vec.add(res);//再把数组装进链表
sum = 0;
break;//当前该正整数序列和刚好等于target,无须再加下去了
}
}
}
return vec.toArray(new int[vec.size()][]);
}
}法二:枚举+数学优化
class Solution {
public int[][] findContinuousSequence(int target) {
List<int[]> vec = new ArrayList<int[]>();
int sum = 0, limit = (target - 1) / 2; // (target - 1) / 2 等效于 target / 2 下取整
for (int x = 1; x <= limit; ++x) {
long delta = 1 - 4 * (x - (long) x * x - 2 * target);
if (delta < 0) {
continue;
}
int delta_sqrt = (int) Math.sqrt(delta + 0.5);
if ((long) delta_sqrt * delta_sqrt == delta && (delta_sqrt - 1) % 2 == 0) {
int y = (-1 + delta_sqrt) / 2; // 另一个解(-1-delta_sqrt)/2必然小于0,不用考虑
if (x < y) {
int[] res = new int[y - x + 1];
for (int i = x; i <= y; ++i) {
res[i - x] = i;
}
vec.add(res);
}
}
}
return vec.toArray(new int[vec.size()][]);
}
}
法三:双指针
class Solution {
public int[][] findContinuousSequence(int target) {
List<int[]> vec = new ArrayList<int[]>();
for (int l = 1, r = 2; l < r;) {
int sum = (l + r) * (r - l + 1) / 2;
if (sum == target) {
int[] res = new int[r - l + 1];
for (int i = l; i <= r; ++i) {
res[i - l] = i;
}
vec.add(res);
l++;
} else if (sum < target) {
r++;
} else {
l++;
}
}
return vec.toArray(new int[vec.size()][]);
}
}第九题:58.翻转单词顺序
我的答案:(运行失败)
class Solution {
public String reverseWords(String s) {
String[] s2=s.split(" ");
int len=s2.length;
StringBuilder s3=new StringBuilder(s2[len-1]);
for(int i=len-2;i>=0;i--){
s3.append(" ");
s3.append(s2[i]);
}
return s3.toString();
}
}官方答案:
法一:语言特性
class Solution {
public String reverseWords(String s) {
// 除去开头和末尾的空白字符
s = s.trim();
// 正则匹配连续的空白字符作为分隔符分割
List<String> wordList = Arrays.asList(s.split("\\s+"));
Collections.reverse(wordList);
return String.join(" ", wordList);
}
}法二:自行编写对应的函数
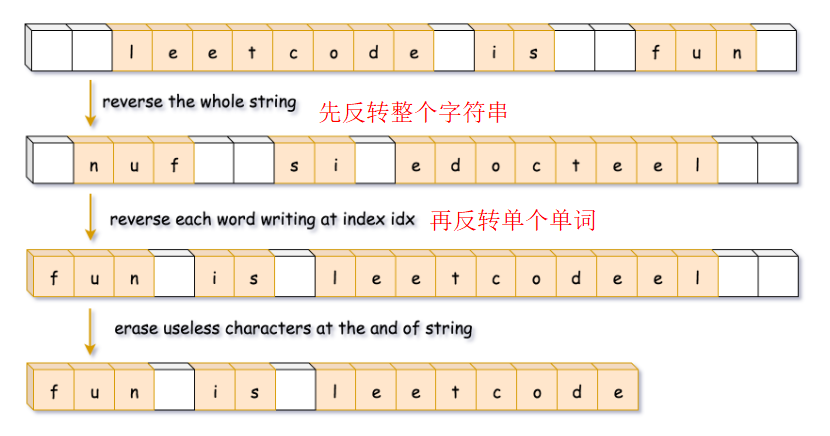
class Solution {
public String reverseWords(String s) {
StringBuilder sb = trimSpaces(s);
// 翻转字符串
reverse(sb, 0, sb.length() - 1);
// 翻转每个单词
reverseEachWord(sb);
return sb.toString();
}
public StringBuilder trimSpaces(String s) {
int left = 0, right = s.length() - 1;
// 去掉字符串开头的空白字符
while (left <= right && s.charAt(left) == ' ') {
++left;
}
// 去掉字符串末尾的空白字符
while (left <= right && s.charAt(right) == ' ') {
--right;
}
// 将字符串间多余的空白字符去除
StringBuilder sb = new StringBuilder();
while (left <= right) {
char c = s.charAt(left);
if (c != ' ') {
sb.append(c);
} else if (sb.charAt(sb.length() - 1) != ' ') {
sb.append(c);
}
++left;
}
return sb;
}
public void reverse(StringBuilder sb, int left, int right) {
while (left < right) {
char tmp = sb.charAt(left);
sb.setCharAt(left++, sb.charAt(right));
sb.setCharAt(right--, tmp);
}
}
public void reverseEachWord(StringBuilder sb) {
int n = sb.length();
int start = 0, end = 0;
while (start < n) {
// 循环至单词的末尾
while (end < n && sb.charAt(end) != ' ') {
++end;
}
// 翻转单词
reverse(sb, start, end - 1);
// 更新start,去找下一个单词
start = end + 1;
++end;
}
}
}法三:双端队列
class Solution {
public String reverseWords(String s) {
int left = 0, right = s.length() - 1;
// 去掉字符串开头的空白字符
while (left <= right && s.charAt(left) == ' ') {
++left;
}
// 去掉字符串末尾的空白字符
while (left <= right && s.charAt(right) == ' ') {
--right;
}
Deque<String> d = new ArrayDeque<String>();//把单词压入队列中
StringBuilder word = new StringBuilder();//StringBuilder的长度可变,更方便
while (left <= right) {
char c = s.charAt(left);
if ((word.length() != 0) && (c == ' ')) {
// 将单词 push 到队列的头部
d.offerFirst(word.toString());
word.setLength(0);
} else if (c != ' ') {
word.append(c);
}
++left;
}
d.offerFirst(word.toString());//把String类型的字符串转成StringBuilder类型的字符串,才能追加到StringBuilder类的
return String.join(" ", d);
}
}第十题:58.左旋字符串

我的答案:
法一:string的函数
(一)concat()函数
class Solution {
public String reverseLeftWords(String s, int n) {
int len=s.length();
String s2=new String();
s2="";
return s2.concat(s.substring(n,len)).concat(s.substring(0,n));
}
}
(二)replace()函数
class Solution {
public String reverseLeftWords(String s, int n) {
return s.replace(s,(s.substring(n,s.length())).concat(s.substring(0,n)));
}
}
网友答案:
法一:+运算符拼接
class Solution {
public String reverseLeftWords(String s, int n) {
return s.substring(n, s.length()) + s.substring(0, n);
}
}法二:append函数拼接
class Solution {
public String reverseLeftWords(String s, int n) {
StringBuilder res = new StringBuilder();
for(int i = n; i < n + s.length(); i++)
res.append(s.charAt(i % s.length()));
return res.toString();
}
}法三:遍历字符串
class Solution {
public String reverseLeftWords(String s, int n) {
String res = "";
for(int i = n; i < n + s.length(); i++)
res += s.charAt(i % s.length());
return res;
}
}第十一题:62.圆圈中最后剩下的数字
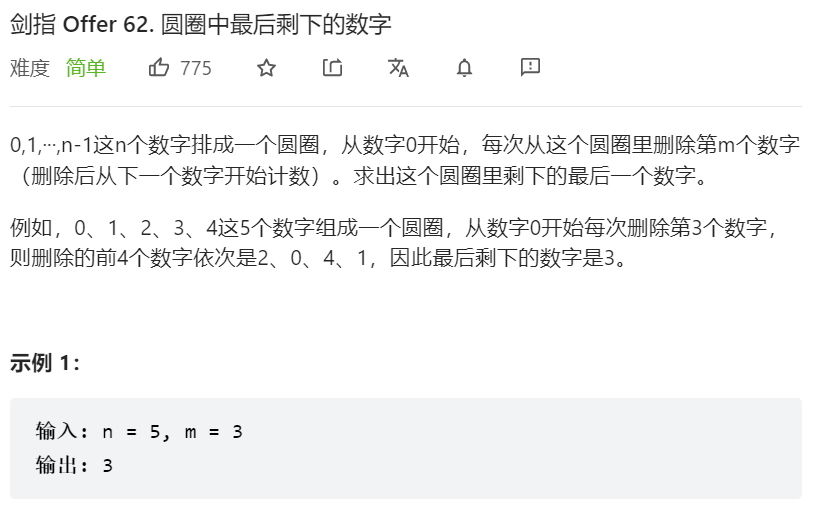
我的答案:队列(超出时间限制)
class Solution {
public int lastRemaining(int n, int m) {
Queue<Integer> queue=new LinkedList<>();
for(int i=0;i<n;i++){
queue.offer(i);
}
int counts=0;//计数器
int t=m;
while(queue.size()!=1){
if(counts==0){//新的一轮
t=m;
while(t>queue.size()){//省略前面重复的对队列的全部遍历,应该用取余更简洁
t=t-queue.size();
}
}
int tmp=queue.poll();//把队列里最早的元素弹出来
counts++;//统计当前元素是第几个元素
if(counts!=t){
queue.offer(tmp);//该元素不是第m个元素,又在队尾处压回队列里
}else{//弹出的元素算是删除了,不再入队
counts=0;//删掉元素后,重置计数器
}
}
return queue.poll();//队列里只剩下一个元素,直接返回
}
}官方答案:
法一:数学+递归
1、长度为
n的序列会先删除第m % n个元素,然后剩下一个长度为n - 1的序列2、取余是为了去掉重复的遍历,如n=10,m=17时,第一遍从0遍历到9是没有意义的,只有从第10到第17时才有意义。
class Solution {
public int lastRemaining(int n, int m) {
return f(n, m);//将问题建模为函数f(n, m),该函数的返回值为最终留下的元素序号
}
public int f(int n, int m) {
if (n == 1) {
return 0;
}
int x = f(n - 1, m);
return (m + x) % n;//(当前index + m) % 上一轮剩余数字的个数
}
}法二:数学+迭代
递归可以改写为迭代,避免递归使用栈空间
class Solution {
public int lastRemaining(int n, int m) {
int f = 0;
for (int i = 2; i != n + 1; ++i) {
f = (m + f) % i;
}
return f;
}
}第十二题:61.扑克牌中的顺子
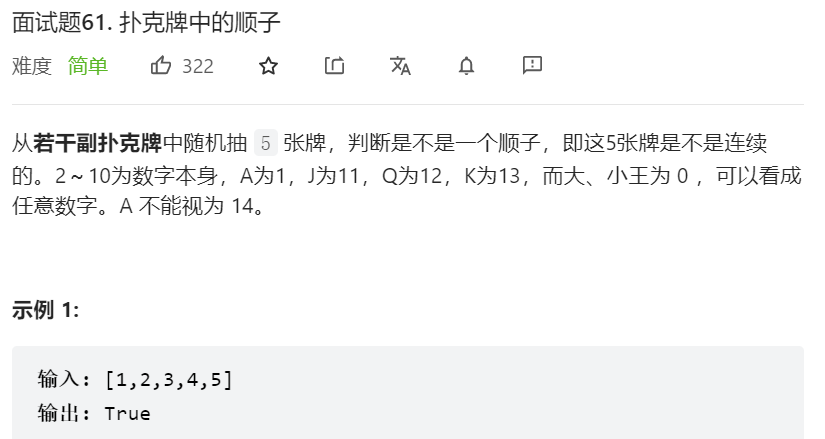
我的答案:排序+遍历
class Solution {
public boolean isStraight(int[] nums) {
int counts1=0;//统计0的个数
int counts2=0;//统计空缺的数字位置数量
Arrays.sort(nums);//将数组按升序排序
for(int i=0;i<4;i++){
if(nums[i]==0){//因为数组已经排序过,所以0的个数最先被统计完
counts1++;
continue;
}
if(nums[i+1]-nums[i]!=1){//判断两个数字是否是相邻数字
counts2+=nums[i+1]-nums[i]-1;
if(counts2>counts1){
return false;
}
}
if(nums[i+1]==nums[i]&&nums[i]!=0){//有两个相等,且不为0的数,这组数字一定不是顺子
return false;
}
}
if(counts1>=counts2) return true;//0的数量永远得比空缺的数字位置要多才行
return false;
}
}
//减少一个变量后
class Solution {
public boolean isStraight(int[] nums) {
int counts1=0;//统计0的个数
Arrays.sort(nums);//将数组按升序排序
for(int i=0;i<4;i++){
if(nums[i]==0){//因为数组已经排序过,所以0的个数最先被统计完
counts1++;
continue;
}else if(nums[i+1]==nums[i]){
return false;
}
if(nums[i+1]-nums[i]!=1){//判断两个数字是否是相邻数字
counts1-=nums[i+1]-nums[i]-1;//nums[i+1]-nums[i]-1统计的是空缺的数字位置数量,直接拿统计好的0的个数减
if(counts1<0){
return false;
}
}
}
if(counts1>=0) return true;//0的数量永远得比空缺的数字位置要多才行
return false;
}
}
网友答案:
顺子要满足两个条件:
1、无重复的牌(大小王除外)
2、最大牌 - 最小牌 < 5
法一:集合Set+遍历
class Solution {
public boolean isStraight(int[] nums) {
Set<Integer> repeat = new HashSet<>();
int max = 0, min = 14;
for(int num : nums) {
if(num == 0) continue; // 跳过大小王
max = Math.max(max, num); // 最大牌
min = Math.min(min, num); // 最小牌
if(repeat.contains(num)) return false; // 若有重复,提前返回 false
repeat.add(num); // 添加此牌至 Set
}
return max - min < 5; // 最大牌 - 最小牌 < 5 则可构成顺子
}
}
法二:排序+遍历
class Solution {
public boolean isStraight(int[] nums) {
int joker = 0;
Arrays.sort(nums); // 数组排序
for(int i = 0; i < 4; i++) {
if(nums[i] == 0) joker++; // 统计大小王数量
else if(nums[i] == nums[i + 1]) return false; // 若有重复,提前返回 false
}
return nums[4] - nums[joker] < 5; // 最大牌 - 最小牌 < 5 则可构成顺子
}
}