昨天是简单的了解了一下支持向量机要干什么以及线性可分支持向量机是怎么一回事,今年来看另一种:线性支持向量机:
我们昨天说的,线性可分支持向量机的目的就是找到一个超平面来吧一个数据集分成正负两个部分,但是实际上,这应该来说是一种理想情怀,因为实际的数据集中往往带有噪声,这就使得数据变成了线性不可分,这种情况之下,就要考虑线性支持向量机。
在前者的基础上,线性支持向量机引入了松弛变量,对于样本点,线性支持向量机是允许部分样本落入超平面H1或者H2的,而前者,要求样本集中的所有样本都要满足:
这个时候,H1和H2之间的距离被称为硬间距,而在线性支持向量机中,
我们允许部分样本越过超平面H1或者H2,这个时候,H1和H2之间的距离被称为软间距。
优化线性支持向量机的时候,目标是软间隔尽可能的大,同时希望越过两个超平面的样布不要远离这两个超平面,,这样的话,我们优化后的目标函数就是:
其中,C是惩罚系数,前者控制最小间隔应尽可能的大,后者求和则控制着越过超平面的样本点离超平面尽量近,C是对着二者关系的权衡,线性支持向量机的优化问题可以写为:
求解就类似于之前的线性可分支持向量机,
然后令lag函数对求偏导,并且令导数为0即可。
和线性可分支持向量机不同的是,线性支持向量机的支持限量并不一定就在H1或者H2上。
我们这里看个简单的示意图吧:

就是说,一个数据集合里面有这些元素,咱要做的,就是和上面图片中的那条黑线一样,找到超平面,然后对集合元素所属属性进行判别。
然后来看一下合页损失函数
对于一个变量下,合页损失函数的定义如下:
对于线性支持向量机,优化问题就相当于优化下式:
其中,前者是合页损失形式
在线性支持向量机中,上式和是等价的。
核函数,就不做过多讲解了,可以简单的立即成一个映射函数,把样本从输入空间映射到特征空间,这样的话,就比较好计算。
一般来说,常见的核函数有:
1、线性核函数,就是支持向量机中的形式:
2、多项式核函数,其中p是超参数
3、高斯核函数,又被称为径向基(RBF)函数,其中,sigma是超参数:
说白了,就是一些实际应用中,你会发现,数据集的混乱程度可谓令人发指,想要直接分类,太难了,太难了怎么办,换个战场呗,将数据集映射到一个比较容易进行分类的空间,然后在用支持向量机进行分类,这不就ok了,简单且实用,对吧。
然后我们最后来看一下二分类和多分类问题,就是说,我们之前这两张讨论的都是二分类,一正一负就没了,实际情况却是多类,那怎么办呢,我们在这里使用一种策略,叫拆解法,典型的拆解法有:一对一(OvO),一对多(OvM),多对多(MvM)。
OvO:我们把K哥类别两两配对,这就得到了K(K-1)/2个二分类任务,然后再测试阶段新样本将同时提交给所有的分类器,就得到了K(K-1)/2个分类结果,最终把预测最多的结果作为投票结果。
OvM:将每一个类别分别作为正类,其他类别作为反类,来训练,这样子的话,只需要K个训练器,说白了,就是每次找个正类,其他的,管你是啥,全是反类,就这么训练,就得到了多个分类结果。
MvM:这个,说实话,我看了很懵,扯到纠错输出码上去了,第一眼还以为是海明码,编码阶段,我们对K个类别进行M次划分,每次将一部分作为正类,另一部分作为反类,编码矩阵有两种形式,二元码,三元码,前者只有正反类,后者还包括了停用类,解码阶段,我们把各分类器的预测结果联合起来形成测试示例的编码,该编码域各类所对应的编码进行比较,将距离最近的编码所对应的类别作为预测结果。
最后,我们看一下,书上用SVM来实现的红葡萄酒分类:
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
if __name__=='__main__':
wine=load_wine()
x_train,x_test,y_train,y_test=train_test_split(wine.data,wine.target)
model=SVC(kernel='linear')
model.fit(x_train,y_train)
train_score=model.score(x_train,y_train)
test_score=model.score(x_test,y_test)
print("train_score:",train_score)
print("test_score:",test_score)这里的核函数kernel是可以更改的:
linear:线性核函数
poly:多项式核函数
rbf:高斯核函数
sigmod:sigmod核函数
precomputed:提前计算好的核函数矩阵
注意: The 'kernel' parameter of SVC must be a str among {'poly', 'sigmoid', 'precomputed', 'rbf', 'linear'} or a callable!!!
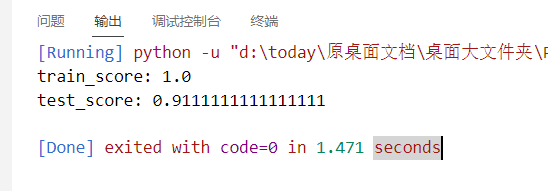
我们来看看不同的核函数效果都怎么样:
linear:
poly:
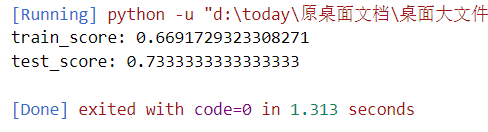
rbf:

sigmod:
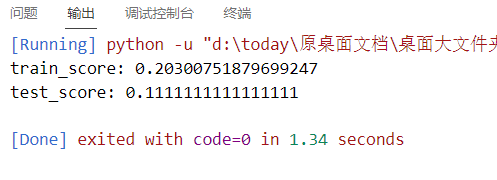
precomputed:
报错了,估计这个用不了
Precomputed matrix must be a square matrix。
不过从上面的四个核函数训练结果来看,红酒集应该是适用线性核函数的,因为,后面的三个,训练和测试得分,emm,实在是,emm,对吧。
好了,SVM就到这里了,基本上把涉及到的都写了,至于推公式,我觉得,这都不是重点了。





![[图神经网络]视觉图神经网络ViG(Vision GNN)--论文阅读](https://img-blog.csdnimg.cn/181c35f2d8cf4bc3b252f1eb9d3d1140.png)
![Docker快速搭建SkyWalking[ OAP UI[登录] Elasticsearch]](https://img-blog.csdnimg.cn/9c29e07ba0144fb6a772715540c6550f.png)