数据结构的加强甜点-序列1

news2024/11/19 10:46:02

尾递归

问题

介绍

特点

原理

答案

数组栈堆内存分配

前言

分析

再分析

所谓多维数组

程序局部性原理应用

尾递归

问题

在空间复杂度这块，有个O(n)示例如下：

void recur(int n) {
    if (n == 1) return;
    return recur(n - 1);
}

这很明显是个尾递归，未啥没优化成O(1)

介绍

在传统的递归中，典型的模型是首先执行递归调用，然后获取递归调用的返回值并计算结果
以这种方式，在每次递归调用返回之前，你不会得到计算结果
这样做的缺点有二：
效率低，占内存
如果递归链过长，可能会statck overflow
若函数在尾位置调用自身（或是一个尾调用本身的其他函数等等），则称这种情况为尾递归
尾递归也是递归的一种特殊情形
尾递归是一种特殊的尾调用，即在尾部直接调用自身的递归函数

特点

对尾递归的优化也是关注尾调用的主要原因
尾递归在普通尾调用的基础上，多出了2个特征：
在尾部调用的是函数自身（Self-called）；
可通过优化，使得计算仅占用常量栈空间 (Stack Space)

原理

当编译器检测到一个函数调用是尾递归的时候，它就覆盖当前的活动记录而不是在栈中去创建一个新的
编译器可以做到这点，因为递归调用是当前活跃期内最后一条待执行的语句，于是当这个调用返回时栈帧中并没有其他事情可做，因此也就没有保存栈帧的必要了
通过覆盖当前的栈帧而不是在其之上重新添加一个，这样所使用的栈空间就大大缩减了，这使得实际的运行效率会变得更高

答案

这段代码是尾递归，理论上可以将空间复杂度优化至O(1)
不过绝大多数编程语言（例如 Java, Python, C++, Go, C# 等）都不支持自动优化尾递归，因此在这里写O(n)

数组栈堆内存分配

前言

栈内存分配由编译器自动完成，而堆内存由程序员在代码中分配（请注意这里的栈和堆不是数据结构中的栈和堆）
1.栈不灵活，分配的内存大小不可更改；堆相对灵活，可以动态分配内存；
2.栈是一块比较小的内存，容易出现内存不足；堆内存很大，但是由于是动态分配，容易碎片化，管理堆内存的难度更大、成本更高；
3.访问栈比访问堆更快，因为栈内存较小、对缓存友好，堆帧分散在很大的空间内，会出现更多的缓存未命中；

分析

假设刚开始，堆、栈是空的
1---声明数组：
int[] array = null;
array只是声明而已，会在栈为其开辟一个空间，堆为开辟空间
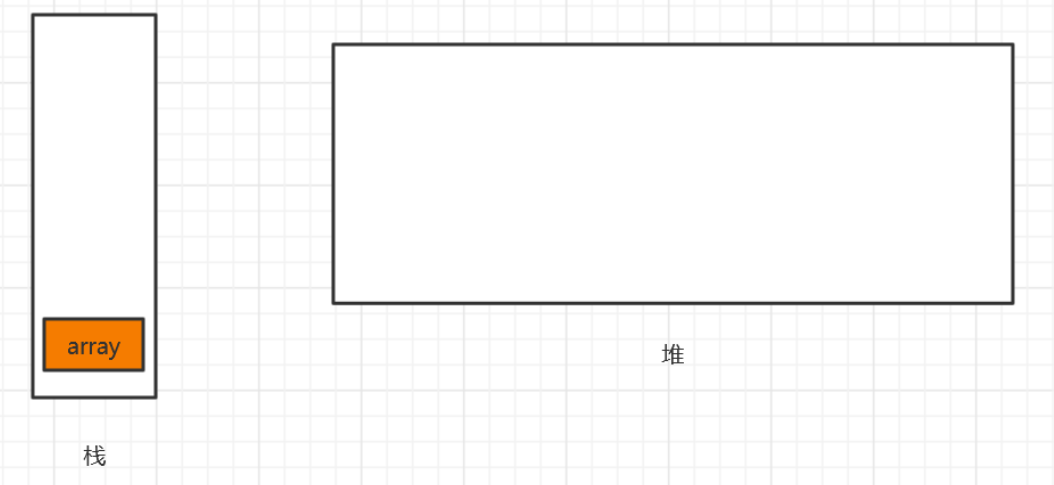
2---创建数组：
array = new int[10];
创建数组，在堆里面开辟空间储存数组，同时栈中的array指向该存储空间

3---给数组赋值：
for(int i = 0; i < 10; i++) array[i]=i+1;

再分析

int[] a = {2,3,4};
int[] b = new int[4];
b = a;

// 定义Person类
public class Person {                                                  
	public int age;
	public double height;
    public void info() {
            System.out.println("年龄：" + age + ",身高：" + height);
    }
}

// 测试类
public class ArrayTest {           
    public static void main(String[] args) {

        // 定义一个students数组变量，其类型是Person[]
        Person[] students = new Person[2];

        Person zhang = new Person();
        zhang.age = 10;
        zhang.height = 130;

        Person lee = new Person();
        lee.age = 20;
        lee.height = 180;

        //将zhang变量赋值给第一个数组元素
        students[0] = zhang;
        //将lee变量赋值给第二个数组元素
        students[1] = lee;

        //下面两行代码结果一样，因为lee和student[1]
        //指向的是同一个Person实例
        lee.info();
        students[1].info();
    }
}

Person[] students = new Person[2] 时

Person zhang = new Person();
zhang.age = 10;
zhang.height = 130;
Person lee = new Person();
lee.age = 20;
lee.height = 180; 时

将zhang变量赋值给第一个数组元素
students[0] = zhang;
将lee变量赋值给第二个数组元素
students[1] = lee; 时

所谓多维数组

先说结论：
Java语言里提供了支持多维数组的语法
如果从数组底层的运行机制上来看，没有多维数组！
开始讲解：
Java里数组是引用类型，因此数组变量其实是一个引用
什么是引用？
引用=起个别名；并不另外开辟内存单元；但占用内存的同一位置
什么是引用类型？
值类型直接存储其值，而引用类型存储对其值的引用
这个引用指向真实的数组内存，如果数组元素也是引用类型，也就是多维数组
那是不是最终都指向一维数组的内容
举例说明：
定义一个二维数组，当作一维数组遍历
结果为null null null null,
说明二维数组其实就是一维数组里元素的引用类型
即一个长度为2的数组

// 定义一个二维数组
int[][] a;
// 把a当作一维数组进行初始化，初始化a是一个长度为4的数组
// a数组的元素又是引用类型
a = new int[4][];
// 把a当作一维数组进行遍历，遍历a的每个元素
for (int i = 0; i < a.length; i++) {
    System.out.println(a[i]);// null null null null
}
// 初始化a的第一个元素
a[0] = new int[2];
// 访问a数组的第一个元素所指向数组的第二个元素
a[0][1] = 6;
// a数组的第一个元素是一个一维数组，遍历这个一维数组
for (int i = 0; i < a[0].length; i++) {
    System.out.println(a[0][i]);
}

int[][] a;
a = new int[4][]; 时
a[0] = new int[2];
a[0][1] = 6; 时
程序采用动态初始化a[0]数组，
因此系统将为a[0]所引用数组的每个元素默认分配0，
程序显示的将a[0]的第二个元素赋值为6
再举例：
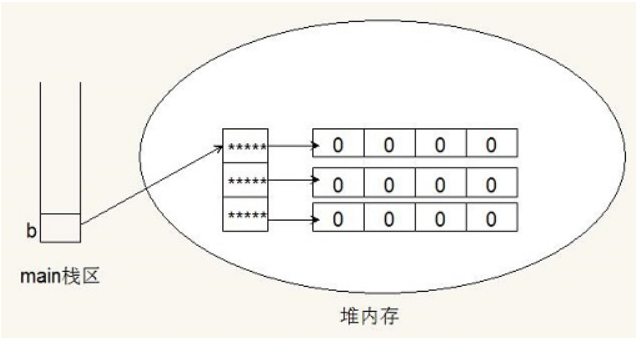
int[][] b = new int[3][4];
同时初始化二维数组的两个维数
该代码定义了一个b数组变量，这个数组变量指向一个长度为3的数组
这个数组的元素又是一个数组类型，它们各指向对应长度为4的int[]数组
每个数组元素的值为0

程序局部性原理应用

除了查找性能链表不如数组外
还有一个优势让数组的性能高于链表,即程序局部性原理
这里简介一下，这属于组成原理的内容
我们知道 CPU 运行速度是非常快的，如果 CPU 每次运算都要到内存里去取数据无疑是很耗时的
所以在 CPU 与内存之间往往集成了挺多层级的缓存，这些缓存越接近CPU，速度越快
所以如果能提前把内存中的数据加载到如下图中的 L1, L2, L3 缓存中，那么下一次 CPU 取数的话直接从这些缓存里取即可，能让CPU执行速度加快
那什么情况下内存中的数据会被提前加载到 L1,L2,L3 缓存中呢
答案是当某个元素被用到的时候，那么这个元素地址附近的的元素会被提前加载到缓存中
以整型数组 1，2，3，4为例
当程序用到了数组中的第一个元素（即 1）时
由于 CPU 认为既然 1 被用到了，那么紧邻它的元素 2，3，4 被用到的概率会很大，所以会提前把 2，3，4 加到 L1,L2,L3 缓存中去，这样 CPU 再次执行的时候如果用到 2，3，4，直接从 L1,L2,L3 缓存里取就行了，能提升不少性能