一、例程概述

本例程是使用节点编辑器建立一个 M/M/1 队列模型，同时对仿真收集到的统计数据进行数学分析。M/M/1 队列由先进先出的缓冲区组成，数据包的到达服从指数(泊松)分布，被称为服务台的处理机以设定的服务速率将数据包从缓冲区头部取出并进行处理。
M/M/1 队列的性能由以下几个参数决定：数据包到达速率；数据包大小；服务容量。
如果数据包的平均到达速率和平均大小结合起来超过了队列的服务容量，则队列将不再稳定。不稳定的队列在实际运用中是没有意义的。
M/M/1 队列输入过程：呼叫源无限，呼叫单个到来且相互独立，在一定时间内到达数服从泊松分布，到达过程是平稳的；
M/M/1 队列排队规则：单对列，队长不受限，先到先服务；
M/M/1 队列处理机构：单处理器，各呼叫处理时间相互独立，服从相同的指数分布。
M/M/1 队列的参数设置：
平均到达速率 $λ=\frac{1}{平均间隔时间}$ ，平均间隔时间= $\frac{1}{λ}$ ，本例程设置为1。
平均服务需求 $\frac{1}{μ}$ ，本例程中设置为9000。
服务容量 C = 9600
平均服务速率 μC ≈ 1.067
平均延时 $D=\frac{1}{μC-λ} ≈ 15$ s
平均队列长度 $L=\frac{λ}{μC(1-\frac{λ}{μC})} ≈ 15$
本文还会改变平均间隔时间进行对比；将无限长队列修改为有限长队列；在 M/M/1 队列的基础上进行 M/M/n 队列的建模和仿真。

二、模型构建

节点模型如下图所示。
在这里插入图片描述
src 的进程模型为 simple_source，如下图所示。

src 处理器的属性设置如下。

queue 的进程模型为 acb_fifo，如下图所示。

“a”表明它是活动(Active)的；“c”表明它可以将多个到来的数据包流集中到其唯一的排队资源上；“b”表明服务时间是数据包比特长度的函数；“fifo”表明服务次序是先进先出。
queue 队列的属性设置如下。
在这里插入图片描述
sink 的进程模型为 sink，如下图所示。

节点接口只选择固定节点，在网络模型中找到上面新建的节点模型放置在项目场景中即可。

三、仿真配置及结果

设置仿真时长为 7 小时，随机数种子为 431，然后就可以开始运行仿真了，仿真的结果以 time_average 显示结果。

1.M/M/1 队列

队列延时的时间平均曲线如下图。
在这里插入图片描述
由上图可以看到，仿真开始时曲线的变化比较剧烈，随着仿真时间的推进，平均延时趋近于一个稳定值15，这与前面理论计算的结果一致。
队列长度的时间平均曲线如下图。

队列长度曲线的走向与延时的走向大体一致，最终其平均值也稳定在15左右，与理论计算的结果吻合。
将队列长度与平均延时绘制在一起可以发现，随着队列长度的增加，平均延时也会跟着增加，如下图所示。
在这里插入图片描述
将队列的包容量设置为35，其结果如下图所示。

将队列的包容量设置为20，其结果如下图所示。

可以看到，随着无限长队列变为有限长队列，队列的平均延时也会跟着减小。

2.M/M/n 队列

队列无限长的情况下，将处理器的数量设置为 2(需要修改queue节点的进程模型)，其仿真结果如下图所示。
在这里插入图片描述
将处理器的数量设置为 5，其仿真结果如下图所示。

可以看到，对于无限长队列，增加处理器的数量也会使得平均延时减小。
平均间隔时间为1，即指数函数为 exponential(1) 的结果如下图所示。

平均间隔时间为2.5，即指数函数为 exponential(2.5) 的结果如下图所示。
在这里插入图片描述
以上两个曲线说明在其他条件不变的情况下，系统是稳定的，而且稳态下数据包平均延时和队列长度随着平均间隔时间的增加而降低。
平均间隔时间为 0.8 时的结果如下图所示。

可以看到，这种情况况下队列不再稳定，也就是超过了当前队列的服务容量，这时可以通过增加处理器的数量来改善。
平均间隔时间 0.8 的情况下，增加服务器的数量为 2 得到下图所示的结果。
在这里插入图片描述
平均间隔时间 0.8 的情况下，增加服务器的数量为 5 得到下图所示的结果。

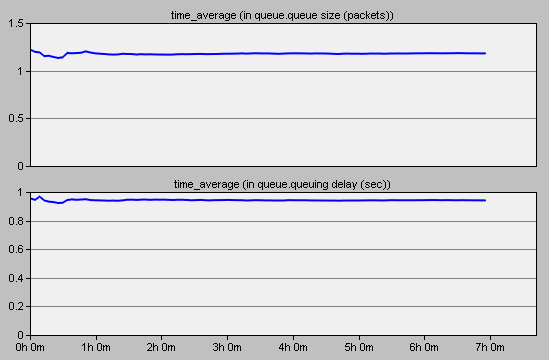
可以看到，增加服务器的数量可以使得队列快速达到稳定，而且随着服务器数量的增加，队列长度的平均和平均延时都会减小。