文章目录
- 1、何为后缀数组
- 2、暴力生成后缀数组
- 3、用DC3算法生成后缀数组的流程
- 4、DC3算法代码实现
- C++版
- Java版
- 5、DC3算法的地位
1、何为后缀数组
假设有一个字符串 “aabaabaa”,从每个位置开始往后到最后一个位置得到的所有的「后缀字符串」”
- 下标7开头:“a”
- 下标6开头:“aa”
- 下标5开头:“baa”
- 下标4开头:“abaa”
- 下标3开头:“aabaa”
- 下标2开头:“baabaa”
- 下标1开头:“abaabaa”
- 下标0开头:“aabaabaa”
将这些后缀字符串以字典序从小到大进行排序:
- 0:下标7开头——“a”
- 1:下标6开头——“aa”
- 2:下标3开头——“aabaa”
- 3:下标0开头——“aabaabaa”
- 4:下标4开头——“abaa”
- 5:下标1开头——“abaabaa”
- 6:下标5开头——“baa”
- 7:下标2开头——“baabaa”
将这些排好序的后缀字符串中以哪个下标位置做为起点的记录在数组中,依次就是:
数组:[7, 6, 3, 0, 4, 1, 5, 2]
下标: 0 1 2 3 4 5 6 7
这个数组就是「后缀数组」。
因为后缀字符串的长度都是不同的,所以不可能存在排名相同的情况。
2、暴力生成后缀数组
假设字符串 str 长度为 N。
- 要生成后缀字符串,得从字符串的最后一个位置开始,依次将每个位置下标到最后一个位置下标的字符串进行拷贝,即一个大字符串生成所有后缀字符串的代价为 O ( N 2 ) O(N^2) O(N2);
- 对所有的后缀字符串进行排序,后缀字符串的数量是 N N N,所以排序的时间复杂度为 O ( N l o g N ) O(NlogN) O(NlogN),而在排序过程中涉及到字符串的比较,这个比较的代价和字符串的长度有关,后缀串的平均长度为 N / 2 N/2 N/2,故比较任何两个后缀串的大小的代价或者说每次比较的代价是 O ( N ) O(N) O(N),也就是说排序过程总的时间复杂度为 O ( N l o g N ∗ N ) = O ( N 2 l o g N ) O(NlogN * N) = O(N^2logN) O(NlogN∗N)=O(N2logN)。
所以暴力生成后缀数组的代价为 O ( N 2 l o g N ) O(N^2logN) O(N2logN)。
而利用DC3算法,长度为N的字符串,生成后缀数组的复杂度为 O ( N ) O(N) O(N)。
3、用DC3算法生成后缀数组的流程
之所以叫做DC3是因为这个算法是根据下标模3来进行分组,做一个类似递归的事情,来解决问题。
举例: N N N 个样本( N N N可以巨大),每个样本中有三维数据(数据并不大),现在要对这 N N N个样本进行排序。排序的原则是先根据一维数据排序,小的在前面;如果一维数据一样,则根据二维数据排序,小的在前面;如果二维数据一样,根据三维数据排序,小的在前面。请问,这样的排序怎么做才最快?「基数排序」最快。
基数排序流程讲解
有如下5个样本:
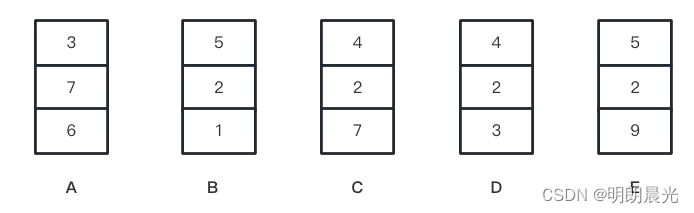
假设每个样本的三维数据值都是在0~9范围的,准备10个桶,编号为0 ~ 9。
-
先根据样本中的第三维数据选择进哪个桶:

从前往后按照桶的编号顺序地将桶中的数据倒出来,得到 [B, D, A, C, E],该顺序是经过第三维数据排序。 -
然后根据当前的[B, D, A, C, E]样本顺序的第二维数据进桶:

依次将桶中的数据倒出,先入先出,得到顺序为 [B, D, C, E, A],该顺序是经过第二维数据排序的。 -
最后根据当前的[B, D, C, E, A]样本顺序的第一维数据进桶:

依次将桶中的数据倒出,得到的顺序为 [A, D, C, B, E],该顺序即是最后的顺序。
由此,可以得到一个结论:N个样本,每个样本的维度不超过3,每个维度的值不太大的时候,可以做到时间复杂度为 O ( N ) O(N) O(N) 的排序,有几个维度就进出桶几次,这是不基于比较的排序。
后缀数组并不局限于字符串,数组也可以求后缀数组
比如整数数组 arr = [103, 56, 27, 103],它的所有后缀数组为:
- 下标0开头:[103, 56, 27, 103]
- 下标1开头:[56, 27, 103]
- 下标2开头:[27, 103]
- 下标3开头:[103]
根据数组中依次的数据大小进行排序得到从小到大为:
- 0:下标2开头——[27, 103] (第一个数是27,所有数组的第1个元素中最小)
- 1:下标1开头——[56, 27, 103]
- 2:下标3开头——[103]
- 3:下标0开头——[103, 56, 27, 103]
所以原数组arr的后缀数组为 [2, 1, 3, 0]。
DC3算法生成后缀数组的流程
首先,将数组/字符串的下标根据 %3 的结果分成三类,%3 结果为0的是 S0 类,结果为1的是 S1 类,结果为2的是 S2 类。
例如:
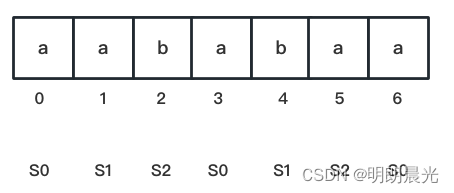
将属于S12类的后缀串选出来:
| 下标 | 后缀串 | 排名 |
|---|---|---|
| 1 | ababaa | 1 |
| 2 | babaa | 3 |
| 4 | baa | 2 |
| 5 | aa | 0(字典序最小) |
如果得到S12类的后缀串排名,就可以得到所有后缀串的总排名。怎么说?
来看S0类的后缀串:0下标开头的后缀串、3下标开头的后缀串、6下标开头的后缀串,现在不知道这三个后缀串的排名情况,但是有了S12类的后缀串排名,就可以得到S0类内部的排名了。
S0类的后缀串,用如下的两维数据表示:
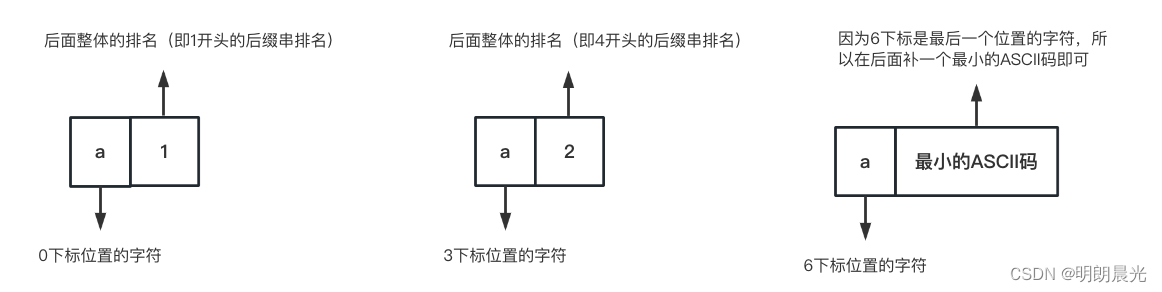
如此一来,0开头的、3开头的和6开头的就两维数据,可以用基数排序了。
所以当有了S12类的排名后,S0内部的排名可以通过一个基数排序直接决定。
可以得到S0类的排名:
| 下标 | 后缀串 | 排名 |
|---|---|---|
| 6 | a | 0(字典序最小) |
| 0 | aababaa | 1 |
| 3 | abaa | 2 |
此时,已经获得了S12类的排名和S0类的排名,要想得到总排名,即S012的排名,只需要像归并排序那样,进行合并操作。
整体逻辑就是:先得到S12类的精确排名,利用它得到S0内部的排名,利用merge 的方式得到总排名。
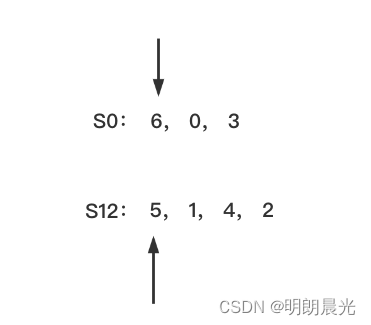
先比较 『6开头的』 VS 『5开头的后缀串』:
- 6开头的后缀串的第一位数据是 a a a,5开头的后缀串的第一位数据是 a a a,没分出大小;
- 但是6开头的后缀串除了 a a a,后面没有数据了;而5开头的后缀串除了 a a a,后面还有数据,说明 6 开头的比 5 开头的字典序小。
- 也就是说 6 开头的是全局最小。
将 6 开头的从S0类中去除:
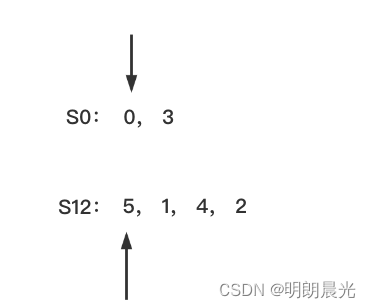
然后是 『0 开头的』 VS 『5开头的后缀串』:
- 0开头的第一位数据是字符 a a a,5开头的第一位数据是字符 a a a,没分出大小;
- 0开头的第二位数据是字符 a a a,5开头的第二位数据是字符 a a a,没分出大小;
- 0开头的后缀串的后面信息(即2开头的后缀串),用排名信息代替:即 a a 3 aa3 aa3;而5开头后面没有信息了,所以5开头的更小。
- 对于更普遍的情况:如果S0类的下标(0开头)和S2类的下标(5开头)后缀串比较大小。
- 比如6开头的要和5开头的后缀串比较大小:
- 首先是6开头的后缀串的第一个字符(即下标6位置的字符)和5开头的第一个字符(即下标5位置的字符)比较,如果比较出了大小,则直接merge;
- 没有比较出大小则继续看下标7位置的字符串 和 下标6位置的字符,如果比较出大小则直接merge;
- 否则后面直接比较 「8位置下标开头的」和 「7位置下标开头」的排名,因为下标7和8都属于S12类,此前已经得到了S12类的排名。
- 只需要比较三次,即进行三次基数排序,必能merge出结果。
- 比如6开头的要和5开头的后缀串比较大小:
- 也就是说:S0类和S2类相遇的时候,最多要比较三维。 (S0 S1 S2) VS (S2 S0 S1)
S0: x x () -> 6开头的: x x (8开头的后缀串排名)
下标类别: S0 S1 S2 下标: 6 7
S2: x x () -> 5开头的: x x (7开头的后缀串排名)
下标类别: S2 S0 S1 下标: 5 6
同理的,S0类和S1类相遇,最多比较两次,两位信息足以merge出来。
结论:如果有S12类的排名,可在 O ( N ) O(N) O(N) 的时间内得到S0内部的排名,再用 O ( N ) O(N) O(N) 的时间合并S0和S12类,得到S012的排名。也就是说只要S12类的排名一旦确定,这个算法就是 O ( N ) O(N) O(N)复杂度的。
问题的关键就变成了「如何得到S12类的排名」?
以字符串 mississippi 为例:
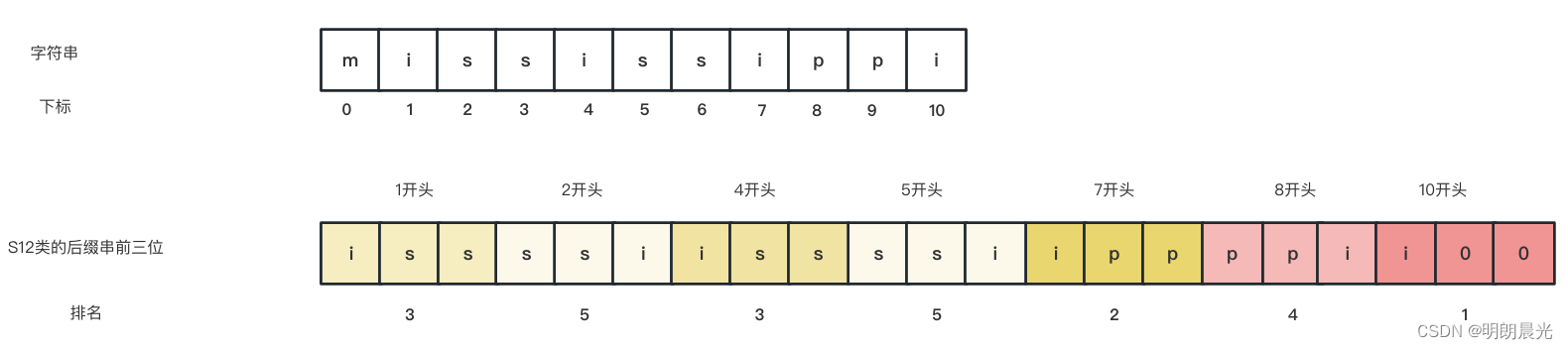
若只用前三维数据就能得到S12类的精准排名,即三次基数排序,则整个算法结束,然后得到S0内部的排名,合并S0、S12类;
但是本例不能用仅三维数据得到S12类的精准排名,因为存在相同排名。那么应该怎么求呢?组成一个新数组,规则是S1类放左边,S2类放右边:
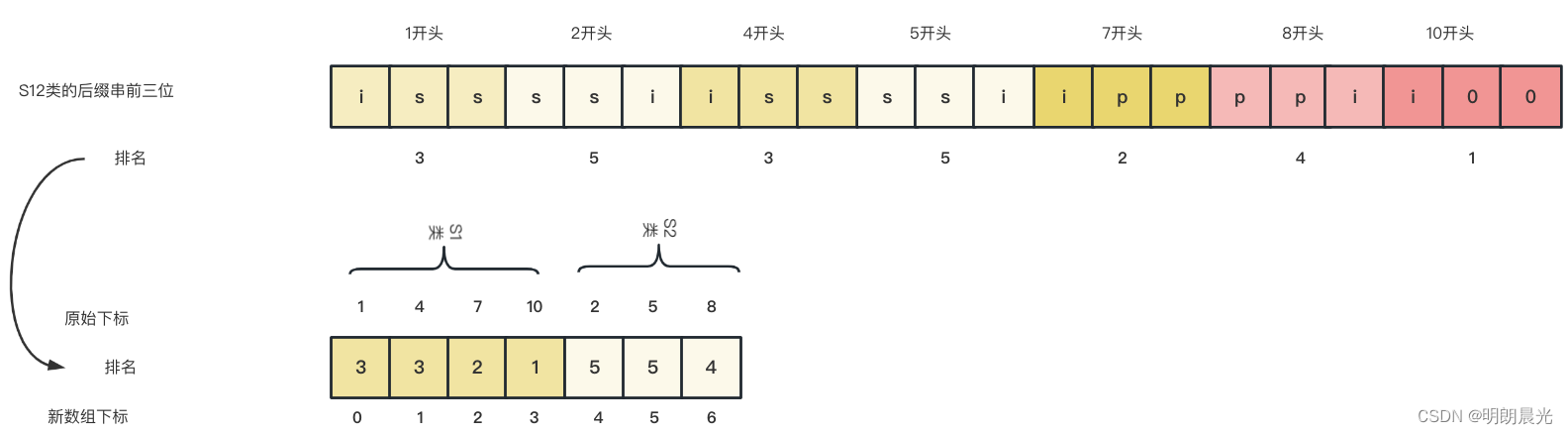
因为任何一个数组都可以求得其后缀数组,所以新数组可以递归调用函数求出其后缀数组,最终得到的「新数组0下标开头的后缀串的排名」就是「原数组1下标开头的后缀串的排名」,「新数组1下标开头的后缀串排名」就是「原数组4下标开头的后缀串排名」,以此类推。也就是「新数组的后缀串的排名」可以指导「原数组后缀串的排名」。

- 第0名是新数组 3 下标开头的,就代表原数组10下标开头的是第0名;
- 第1名是新数组 2 下标开头的,就代表原数组 7 下标开头的是第1名;
- 第2名是新数组 1 下标开头的,就代表原数组 4 下标开头的是第2名;
- 第3名是新数组 0 下标开头的,就代表原数组 1 下标开头的是第3名;
- 第4名是新数组 6 下标开头的,就代表原数组 8 下标开头的是第4名;
- 第5名是新数组 5 下标开头的,就代表原数组 5 下标开头的是第5名;
- 第6名是新数组 4 下标开头的,就代表原数组 2 下标开头的是第6名。
为什么S1类和S2类要分开放置到新数组中,为什么这种方式可以使得之前悬而未决的排名得到精确的结果?
首先,对于那些使用三维数据已经得到排名的数据来说,无论如何将其放置在新数组中,它的相对次序都不会改变,如「1开头的iss」和「5开头的ssi」大小已近分出来了,无论在新数组中这两个排名值如何摆放,相对次序都不会改变。
而将S1类整体放左边,S2类整体放右边,是为了解决相同排名的问题,即在三维数据排名后出现的相同排名问题,如「1开头的iss」和「4开头的iss」都排第3名。「1开头的iss」和「4开头的iss」之所以分不出大小,是因为前三维数据都一样(下标123 和 下标456对应的值),缺的是「4开头的整体排名」和「7开头的整体排名」,而S1类和S2类当前的这种摆放方式,刚好将缺的部分放在了一起,「4开头的整体排名」就用4开头的三维数据的排名3代替了,「7开头的整体排名」用7开头的三维数据排名2代替了,以此类推,这就是DC3算法最精髓的地方。
这种新数组的构建方式不仅可以解决S0类或S1类的内部排名相同问题,也可以解决S0类和S1类排名相同的问题。
举个例子:
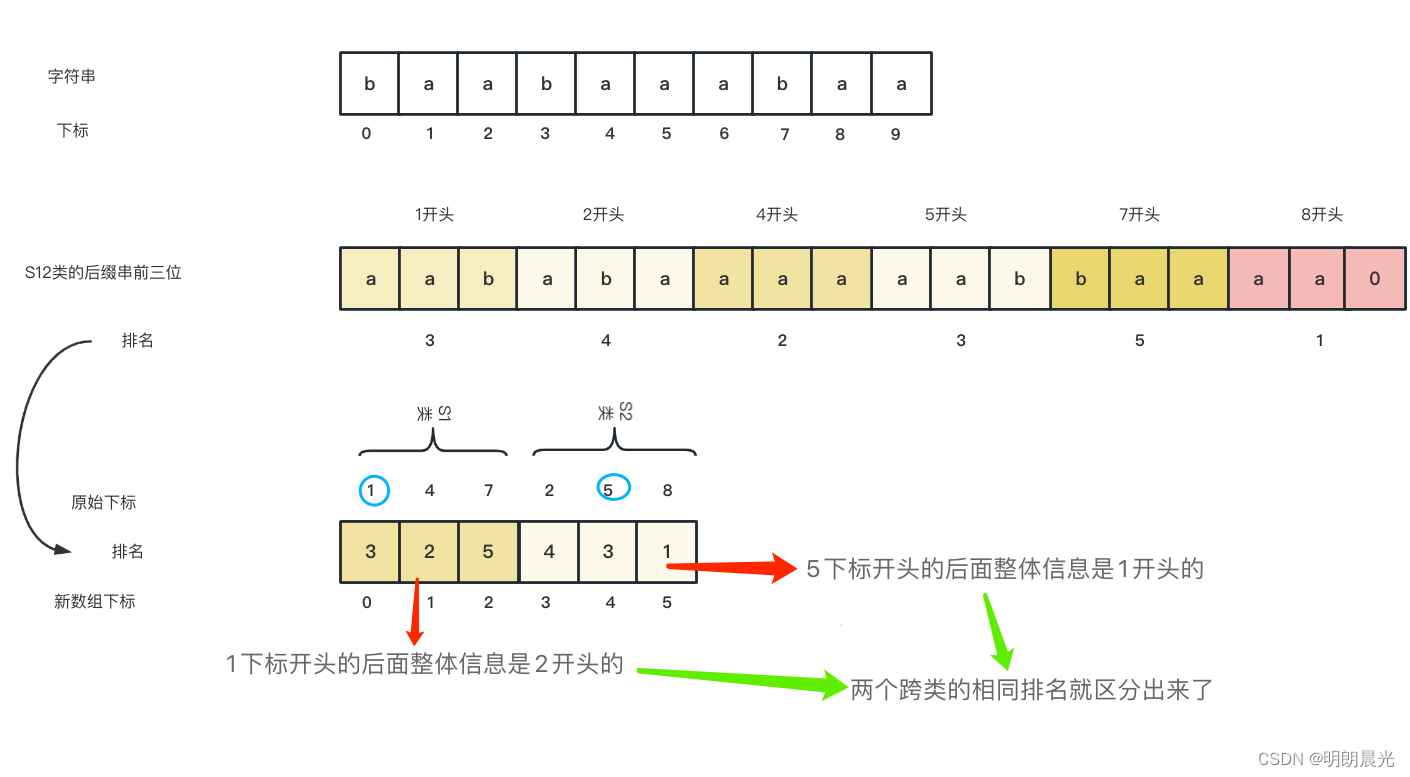
注意,新构造数组的S1类的最后一个位置后面跟的是S2类的第一个位置,就比如数组长度为9,下标0 ~ 8,则构造的新数组中原始下标7开头的后面贴着2开头的后缀串,而原数组中7开头的三维数据后面是没有数据的,而新数组的意思就是7开头的后缀串除了前三维数据后面还跟着2开头的后缀串的信息,对于这种边界问题,会适时地在两个类的分界线上补最小的ASCII码字符,分隔开两个类,以避免产生误解。
小结
- 首先找到S12类的后缀串的前三维数据,如果能通过前三维数据得到精确排名,算法结束;
- 如果不能则要生成新数组,因为只将S12类放在了数组中,假设原数组长度为 N N N,则新数组是原数组长度的 2 / 3 2/3 2/3,即 2 N / 3 2N/3 2N/3,而在这个数组中只放入了排名,排名不会超过 N N N,所以该数组的最大值为 N N N,于是递归调用DC3算法,准备 N N N个桶,进行三次基数排序,就能得到最终的结果。
整体的复杂度 T ( N ) = T ( 2 N / 3 ) + O ( N ) T(N) = T(2N/3) + O(N) T(N)=T(2N/3)+O(N),就是 O ( N ) O(N) O(N) 复杂度。
4、DC3算法代码实现
C++版
//论文源码
inline bool leq(int a1, int a2, int b1, int b2) { // lexicographic order
return(a1 < b1 || a1 == b1 && a2 <= b2);
} // for pairs
inline bool leq(int a1, int a2, int a3, int b1, int b2, int b3) {
return(a1 < b1 || a1 == b1 && leq(a2,a3, b2,b3));
} // and triples
// stably sort a[0..n-1] to b[0..n-1] with keys in 0..K from r
static void radixPass(int* a, int* b, int* r, int n, int K) {
// count occurrences
int* c = new int[K + 1]; // counter array
for (int i = 0; i <= K; i++)
c[i] = 0; // reset counters
for (int i = 0; i < n; i++)
c[r[a[i]]]++; // count occurrences
for (int i = 0, sum = 0; i <= K; i++) // exclusive prefix sums
{
int t = c[i];
c[i] = sum;
sum += t;
}
for (int i = 0; i < n; i++)
b[c[r[a[i]]]++] = a[i]; // sort
delete [] c;
}
// find the suffix array SA of s[0..n-1] in {1..K}ˆn
// require s[n]=s[n+1]=s[n+2]=0, n>=2
void suffixArray(int* s, int* SA, int n, int K) {
int n0=(n+2)/3, n1=(n+1)/3, n2=n/3, n02=n0+n2;
int* s12 = new int[n02 + 3];
s12[n02]= s12[n02+1]= s12[n02+2]=0;
int* SA12 = new int[n02 + 3];
SA12[n02]=SA12[n02+1]=SA12[n02+2]=0;
int* s0 = new int[n0];
int* SA0 = new int[n0];
// generate positions of mod 1 and mod 2 suffixes
// the "+(n0-n1)" adds a dummy mod 1 suffix if n%3 == 1
for (int i=0, j=0; i < n+(n0-n1); i++)
if (i%3 != 0)
s12[j++] = i;
// lsb radix sort the mod 1 and mod 2 triples
radixPass(s12 , SA12, s+2, n02, K);
radixPass(SA12, s12 , s+1, n02, K);
radixPass(s12 , SA12, s , n02, K);
// find lexicographic names of triples
int name = 0, c0 = -1, c1 = -1, c2 = -1;
for (int i = 0; i < n02; i++) {
if (s[SA12[i]] != c0 || s[SA12[i]+1] != c1 || s[SA12[i]+2] != c2) {
name++;
c0 = s[SA12[i]];
c1 = s[SA12[i]+1];
c2 = s[SA12[i]+2];
}
if (SA12[i] % 3 == 1) {
s12[SA12[i]/3] = name;
} // left half
else {
s12[SA12[i]/3 + n0] = name;
} // right half
}
// recurse if names are not yet unique
if (name < n02) {
suffixArray(s12, SA12, n02, name);
// store unique names in s12 using the suffix array
for (int i = 0; i < n02; i++)
s12[SA12[i]] = i + 1;
} else // generate the suffix array of s12 directly
for (int i = 0; i < n02; i++)
SA12[s12[i] - 1] = i;
// stably sort the mod 0 suffixes from SA12 by their first character
for (int i=0, j=0; i < n02; i++)
if (SA12[i] < n0)
s0[j++] = 3*SA12[i];
radixPass(s0, SA0, s, n0, K);
// merge sorted SA0 suffixes and sorted SA12 suffixes
for (int p=0, t=n0-n1, k=0; k < n; k++) {
#define GetI() (SA12[t] < n0 ? SA12[t]*3+1: (SA12[t] - n0) * 3 + 2)
int i = GetI(); // pos of current offset 12 suffix
int j = SA0[p]; // pos of current offset 0 suffix
if (SA12[t] < n0 ? // different compares for mod 1 and mod 2 suffixes
leq(s[i], s12[SA12[t] + n0], s[j], s12[j/3]) :
leq(s[i],s[i+1],s12[SA12[t]-n0+1], s[j],s[j+1],s12[j/3+n0]))
{
// suffix from SA12 is smaller
SA[k] = i; t++;
if (t == n02) // done --- only SA0 suffixes left
for (k++; p < n0; p++, k++) SA[k] = SA0[p];
} else {// suffix from SA0 is smaller
SA[k] = j; p++;
if (p == n0) // done --- only SA12 suffixes left
for (k++; t < n02; t++, k++) SA[k] = GetI();
}
}
delete [] s12;
delete [] SA12;
delete [] SA0;
delete [] s0;
}
Java版
//可作为模板使用
public class DC3 {
public int[] sa; //前文提到的所有后缀数组的排名,sa数组中下标代表排名,值代表每个后缀数组排名后的起始下标
public int[] rank;//每个位置开始的后缀串的排名,rank数组中下标代表原数组中的下标,值表示排名
//如[aaba]
// 1234
//sa:[3, 0, 1, 2] ->下标
// 0 1 2 3 ->排名
//rank:[1, 2, 3, 0] ->排名
// 0 1 2 3 ->下标
//通过sa数组加工得到rank数组的复杂度:O(N)
public int[] height;
// 构造方法的约定:
// 数组叫nums,如果你是字符串,请转成整型数组nums
// 数组中,最小值>=1,做这种限制是因为可能会需要补0
// 如果不满足,处理成满足的,也不会影响使用
// 对于负数数组:[-30, -17, 103]等同于每个数都+31,得到[1, 14, 134],后缀串的排名相同
// max是nums里面最大值,根据max准备桶的数量
public DC3(int[] nums, int max) {
sa = sa(nums, max);
rank = rank();
height = height(nums);
}
private int[] sa(int[] nums, int max) {
int n = nums.length;
int[] arr = new int[n + 3]; //可能会补空,所以多增加了三个长度
for (int i = 0; i < n; i++) {
arr[i] = nums[i];
}
return skew(arr, n, max);
}
private int[] skew(int[] nums, int n, int K) {
int n0 = (n + 2) / 3, n1 = (n + 1) / 3, n2 = n / 3, n02 = n0 + n2; //统计每个类型(S0/S1/S2)的数量,+2,+1 是因为可能会补空
int[] s12 = new int[n02 + 3], sa12 = new int[n02 + 3]; //S12类组成一个数组
for (int i = 0, j = 0; i < n + (n0 - n1); ++i) {
if (0 != i % 3) {
s12[j++] = i;
}
}
//最多三维数据,进行三次基数排序
radixPass(nums, s12, sa12, 2, n02, K);
radixPass(nums, sa12, s12, 1, n02, K);
radixPass(nums, s12, sa12, 0, n02, K);
int name = 0, c0 = -1, c1 = -1, c2 = -1;
for (int i = 0; i < n02; ++i) {
if (c0 != nums[sa12[i]] || c1 != nums[sa12[i] + 1] || c2 != nums[sa12[i] + 2]) {
name++;
c0 = nums[sa12[i]];
c1 = nums[sa12[i] + 1];
c2 = nums[sa12[i] + 2];
}
if (1 == sa12[i] % 3) {
s12[sa12[i] / 3] = name;
} else {
s12[sa12[i] / 3 + n0] = name;
}
}
if (name < n02) { //如果没有得到严格排名,则递归调用
sa12 = skew(s12, n02, name);
for (int i = 0; i < n02; i++) {
s12[sa12[i]] = i + 1;
}
} else {
for (int i = 0; i < n02; i++) {
sa12[s12[i] - 1] = i;
}
}
//此时已经得到S12类的准确排名
//先解决S0内部的排名
int[] s0 = new int[n0], sa0 = new int[n0];
for (int i = 0, j = 0; i < n02; i++) {
if (sa12[i] < n0) {
s0[j++] = 3 * sa12[i];
}
}
radixPass(nums, s0, sa0, 0, n0, K);
//再解决S0和S12类合并的问题
int[] sa = new int[n];
for (int p = 0, t = n0 - n1, k = 0; k < n; k++) {
int i = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
int j = sa0[p];
if (sa12[t] < n0 ? leq(nums[i], s12[sa12[t] + n0], nums[j], s12[j / 3])
: leq(nums[i], nums[i + 1], s12[sa12[t] - n0 + 1], nums[j], nums[j + 1], s12[j / 3 + n0])) {
sa[k] = i;
t++;
if (t == n02) {
for (k++; p < n0; p++, k++) {
sa[k] = sa0[p];
}
}
} else {
sa[k] = j;
p++;
if (p == n0) {
for (k++; t < n02; t++, k++) {
sa[k] = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
}
}
}
}
return sa;
}
private void radixPass(int[] nums, int[] input, int[] output, int offset, int n, int k) {
int[] cnt = new int[k + 1];
for (int i = 0; i < n; ++i) {
cnt[nums[input[i] + offset]]++;
}
for (int i = 0, sum = 0; i < cnt.length; ++i) {
int t = cnt[i];
cnt[i] = sum;
sum += t;
}
for (int i = 0; i < n; ++i) {
output[cnt[nums[input[i] + offset]]++] = input[i];
}
}
private boolean leq(int a1, int a2, int b1, int b2) {
return a1 < b1 || (a1 == b1 && a2 <= b2);
}
private boolean leq(int a1, int a2, int a3, int b1, int b2, int b3) {
return a1 < b1 || (a1 == b1 && leq(a2, a3, b2, b3));
}
private int[] rank() {
int n = sa.length;
int[] ans = new int[n];
for (int i = 0; i < n; i++) {
ans[sa[i]] = i;
}
return ans;
}
private int[] height(int[] s) {
int n = s.length;
int[] ans = new int[n];
for (int i = 0, k = 0; i < n; ++i) {
if (rank[i] != 0) {
if (k > 0) {
--k;
}
int j = sa[rank[i] - 1];
while (i + k < n && j + k < n && s[i + k] == s[j + k]) {
++k;
}
ans[rank[i]] = k;
}
}
return ans;
}
// 为了测试
public static int[] randomArray(int len, int maxValue) {
int[] arr = new int[len];
for (int i = 0; i < len; i++) {
arr[i] = (int) (Math.random() * maxValue) + 1;
}
return arr;
}
// 为了测试
public static void main(String[] args) {
int len = 100000;
int maxValue = 100;
long start = System.currentTimeMillis();
new DC3(randomArray(len, maxValue), maxValue);
long end = System.currentTimeMillis();
System.out.println("数据量 " + len + ", 运行时间 " + (end - start) + " ms");
}
}
5、DC3算法的地位
笔试的时候,通常会有根据算法有以下几种数据通过情况:
- 暴力解,不通过;
- 优化解,假设数据通过70%;
- 出题人给定的答案解,数据通过100%,是根据这个解设置的数据量
但是如果一个题目可以使用DC3算法,那它是碾压答案解的,但是因为DC3算法太难,导致笔试的时候设置的答案解都会选一个比DC3差一点儿的解,这就是DC3算法的地位。