机器学习:基于逻辑回归对优惠券使用情况预测分析
作者:i阿极
作者简介:Python领域新星作者、多项比赛获奖者:博主个人首页
😊😊😊如果觉得文章不错或能帮助到你学习,可以点赞👍收藏📁评论📒+关注哦!👍👍👍
📜📜📜如果有小伙伴需要数据集和学习交流,文章下方有交流学习区!一起学习进步!💪
| 订阅专栏案例:机器学习 |
|---|
| 机器学习:基于逻辑回归对某银行客户违约预测分析 |
| 机器学习:学习k-近邻(KNN)模型建立、使用和评价 |
| 机器学习:基于支持向量机(SVM)进行人脸识别预测 |
| 决策树算法分析天气、周末和促销活动对销量的影响 |
| 机器学习:线性回归分析女性身高与体重之间的关系 |
| 机器学习:基于主成分分析(PCA)对数据降维 |
| 机器学习:基于朴素贝叶斯对花瓣花萼的宽度和长度分类预测 |
| 机器学习:学习KMeans算法,了解模型创建、使用模型及模型评价 |
| 机器学习:基于神经网络对用户评论情感分析预测 |
| 机器学习:朴素贝叶斯模型算法原理(含实战案例) |
| 机器学习:逻辑回归模型算法原理(附案例实战) |
文章目录
- 机器学习:基于逻辑回归对优惠券使用情况预测分析
- 1、实验目的
- 2、实验原理
- 3、实验环境
- 4、数据预处理
- 5、查看特征值于目标值之间的相关关系
- 6、选取特征值
- 7、进行编码后目标值于特征值的相关关系
- 8、查看类别型变量的所有类别及类别分布概率情况
- 9、模型建立
- 10、模型评估
- 总结
1、实验目的
随着人工智能的不断发展,机器学习这门技术也越来越重要,很多人都开启了学习机器学习,本文就介绍了机器学习的基础内容。
在这个信息爆炸的时代,如何高效处理数据并利用数据推动决策显得尤为重要,这便是人们通常所说的“数据分析”。与数据分析相伴而生的机器学习(Machine Learning),有些人可能会感到陌生,然而说到战胜了众多人类围棋高手的智能机器人AlphaGo,想必大多数人都有所耳闻。AlphaGo背后的原理支撑就是机器学习,它通过模拟人类的学习行为,不停地分析海量的围棋数据,发现数据背后的规律,从而在已有条件下做出最为理性的决断,这个过程充满了机器美学。
2、实验原理
逻辑回归模型虽然名字中有回归两字,其本质却是分类模型。
分类模型与回归模型的区别在于其预测的变量不是连续的,而是离散的一些类别,以最常见的二分类模型为例,分类模型可以预测一个人是否会违约、客户是否会流失、肿瘤是属于良性肿瘤还是恶性肿瘤等
逻辑回归模型的算法原理中同样涉及了之前线性回归模型中学习到的线性回归方程:
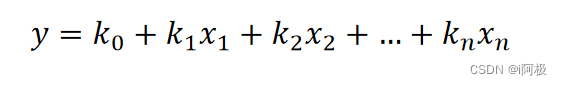
上面这个方程是预测连续变量的,其取值范围属为负无穷到正无穷,而逻辑回归模型是用来预测类别的,比如它预测某物品是属于A类还是B类,它本质预测的是属于A类或者B类的概率,而概率的取值范围是0-1,因此我们不能直接用线性回归方程来预测概率。
需要到用到下图所示的Sigmoid函数,该函数可以将取值为(-∞, +∞)的数转换到(0,1)之间,例如倘若y=3,那个通过Sigmoid函数转换后,f(y)就变成了1/(1+e^-3)=0.95了,这就可以作为一个概率值使用了。
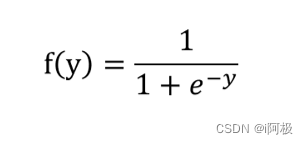
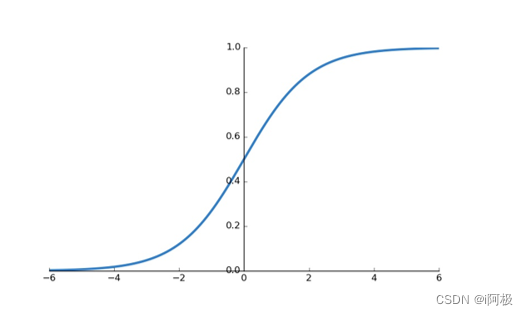
可以通过如下代码绘制Sigmoid函数:
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(-6, 6)
y = 1.0 / (1.0 + np.exp(-x))
plt.plot(x,y)
plt.show()
通过linspace()函数生成-6到6的等差数列,默认50个数.
Sigmoid函数计算公式,exp()函数表示指数函数

如果对Sigmoid函数还是感到有点困惑,则可以参考下图的一个推导过程,其中y就是之前提到的线性回归方程,其范围是(-∞, +∞),那么指数函数的范围便是(0, +∞),再做一次变换,的范围就变成(0, 1)了,然后分子分母同除以就获得了我们上面提到的Sigmoid函数了。
逻辑回归模型本质就是将线性回归模型通过Sigmoid()函数进行了一个非线性转换得到一个介于0到1之间的概率值,对于二分类问题(分类0和1)而言,其预测分类为1(或者说二分类中数值较大的分类)的概率如下图所示:
因为概率和为1,则分类为0(或说二分类中数值较小的那个分类)的概率为1-P:
3、实验环境
Python 3.9
Anaconda
Jupyter Notebook
4、数据预处理
4.1数据说明
| ID | 记录编码 |
|---|---|
| age | 年龄 |
| job | 职业 |
| marital | 婚姻状态 |
| default | 花呗是否有违约 |
| returned | 是否有过退货 |
| loan | 是否使用花呗结账 |
| coupon_used_in_last6_month | 过去六个月使用的优惠券数量 |
| coupon_used_in_last_month | 过去一个月使用的优惠券数量 |
| coupon_ind | 该次活动中是否有使用优惠券 |
4.2导入数据
data = pd.read_csv('/home/mw/L2_Week3.csv')
data.head()

4.3查看数据形状
data.shape

一共有25317行,10列数据
4.4查看数据是否为空值
data.isnull().sum()
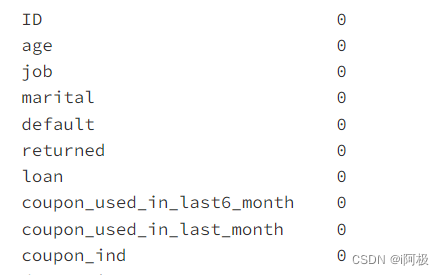
4.5coupon_ind为要预测的目标值,查看目标值的分布情况
data['coupon_ind'].value_counts(1)

5、查看特征值于目标值之间的相关关系
sns.heatmap(data.corr()[['coupon_ind']])
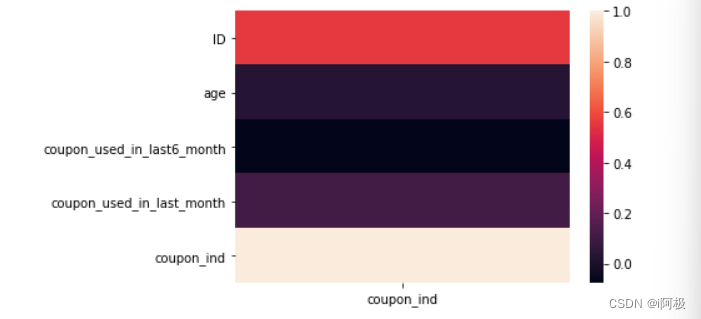
6、选取特征值
6.1选取特征值
X = data.iloc[:,0:9]
X.head()

6.2将类别型变量进行哑变量处理
marital = pd.get_dummies(X['marital'])
job = pd.get_dummies(X['job'])
default = pd.get_dummies(X['default'])
returned = pd.get_dummies(X['returned'])
loan = pd.get_dummies(X['loan'])
6.3将处理好的哑变量于原来的数据按列连接
XX = pd.concat([X,job,marital,default,returned,loan],axis=1)
7、进行编码后目标值于特征值的相关关系
XXX = pd.concat([XX,data['coupon_ind']],axis=1)
sns.heatmap(XXX.corr()[['coupon_ind']])
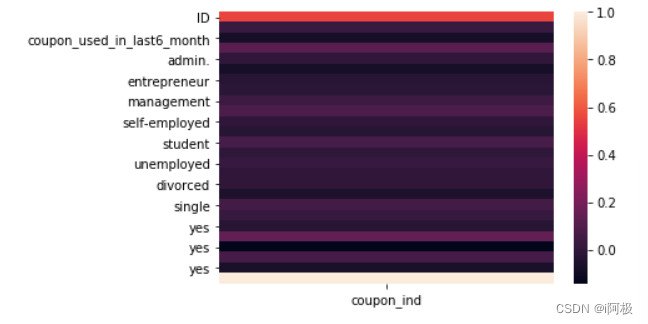
8、查看类别型变量的所有类别及类别分布概率情况
X['job'].unique()

X['marital'].unique()

X['default'].unique()

X['returned'].unique()

X['loan'].unique()
将未进行独热编码的特征删除
x = [2,3,4,5,6]
XX.drop(XX.columns[x], axis=1, inplace=True)
9、模型建立
9.1划分训练集和测试集
XX_train,XX_test,Y_train,Y_test = train_test_split(XX,data['coupon_ind'],train_size=0.75)
9.2训练逻辑回归模型,这里由于目标值样本不均衡,采用加权的方式建立模型
model = LogisticRegression(C=1e4,random_state=100,class_weight='balanced')
model.fit(XX_train, Y_train)
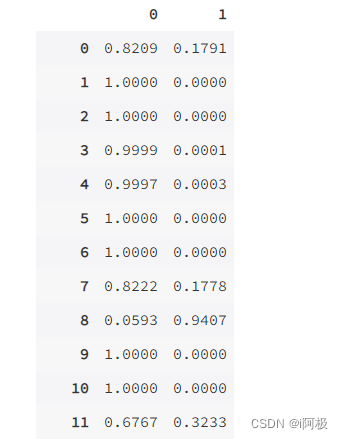
9.3查看训练集的概率
prob = model.predict_proba(XX_train)
pd.DataFrame(prob).apply(lambda x:round(x,4))
10、模型评估
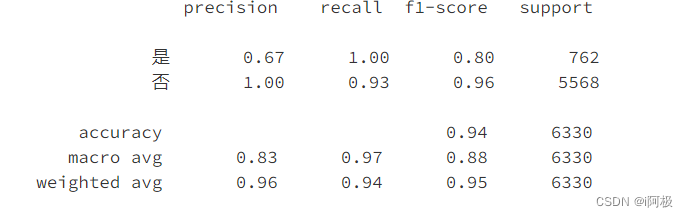
10.1查看预测结果的准确率、召回率、f1-score
pred = model.predict(XX_test)
print(classification_report(Y_test,pred,labels=[1,0],target_names=['是','否']))
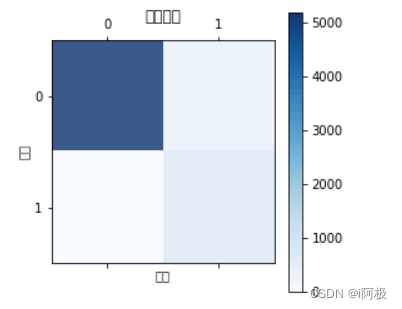
10.2混淆矩阵及可视化
confusion = confusion_matrix(Y_test,pred)
confusion

plt.matshow(confusion,cmap=plt.cm.Blues, alpha=0.8)
plt.title('混淆矩阵')
plt.colorbar()
plt.ylabel('预测')
plt.xlabel('实际')
plt.show()
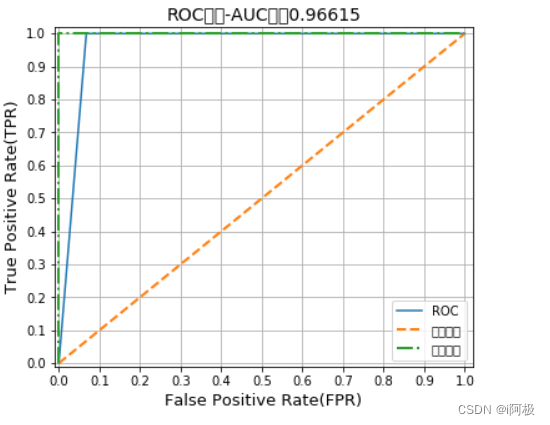
10.3计算ROC曲线AUC值并可视化
from sklearn.metrics import roc_curve,auc
fpr,tpr,threshold = roc_curve(Y_test,pred)
roc_auc = auc(fpr,tpr)
print('ROC曲线AUC值:',roc_auc)

plt.figure(figsize=(6, 5))
# 绘制ROC曲线。
plt.plot(fpr, tpr, label="ROC")
# 绘制(0, 0)与(1, 1)两个点的连线,该曲线(直线)为随机猜测的效果。
plt.plot([0,1], [0,1], lw=2, ls="--", label="随机猜测")
# 绘制(0, 0), (0, 1), (1, 1)三点的连线(两条线),这两条线构成完美的roc曲线(auc的值为1)。
plt.plot([0, 0, 1], [0, 1, 1], lw=2, ls="-.", label="完美预测")
plt.xlim(-0.01, 1.02)
plt.ylim(-0.01, 1.02)
plt.xticks(np.arange(0, 1.1, 0.1))
plt.yticks(np.arange(0, 1.1, 0.1))
plt.xlabel('False Positive Rate(FPR)', fontsize=13)
plt.ylabel('True Positive Rate(TPR)', fontsize=13)
plt.grid()
plt.title(f"ROC曲线-AUC值为{auc(fpr, tpr):.5f}", fontsize=14)
plt.legend()
plt.show()
总结
分类模型与回归模型的区别在于其预测的变量不是连续的,而是离散的一些类别,例如,最常见的二分类模型可以预测一个人是否会违约、客户是否会流失、肿瘤是良性还是恶性等。本章要学习的逻辑回归模型虽然名字中有“回归”二字,但其在本质上却是分类模型。
📢主页:博主个人首页
📢文章下方有交流学习区!一起学习进步!💪💪💪
📢创作不易,你的支持和鼓励是我创作的动力❗❗❗
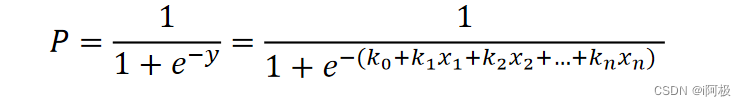
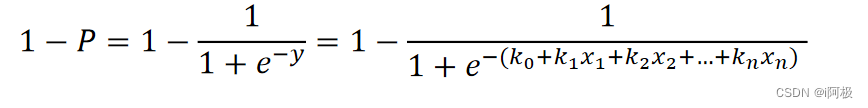




![[ 应急响应基础篇 ] 使用 Autoruns 启动项分析工具分析启动项(附Autoruns安装教程)](https://img-blog.csdnimg.cn/6c995927a42a4e7f972f5914e33f2050.png)