144. 二叉树的前序遍历

给你二叉树的根节点root，返回它节点值的前序遍历。
示例 1：

输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

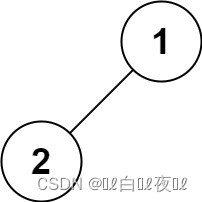
输入：root = [1,2]
输出：[1,2]

示例 5：

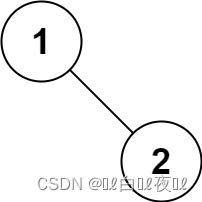
输入：root = [1,null,2]
输出：[1,2]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶：

递归算法很简单，你可以通过迭代算法完成吗？

原题链接：https://leetcode.cn/problems/binary-tree-preorder-traversal/

思路：
将一棵树分成左路节点和左路节点的右子树。

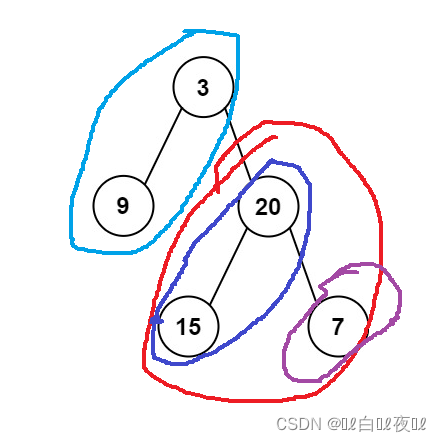
那么迭代如何实现呢？这需要一个栈来储存结点。

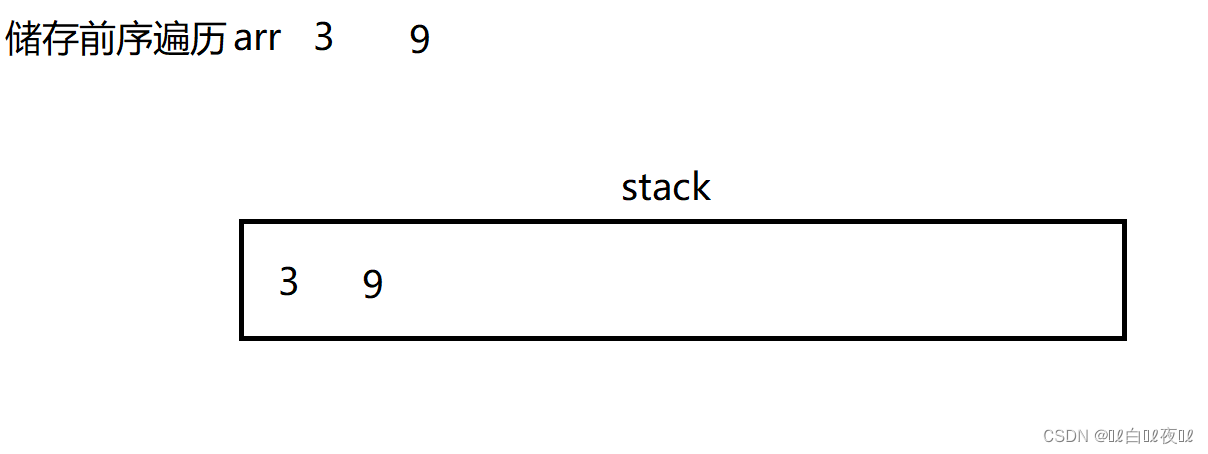
先从头结点，访问到左子树的空为止，但是再这个过程中要将经过的数放进一个数组中。



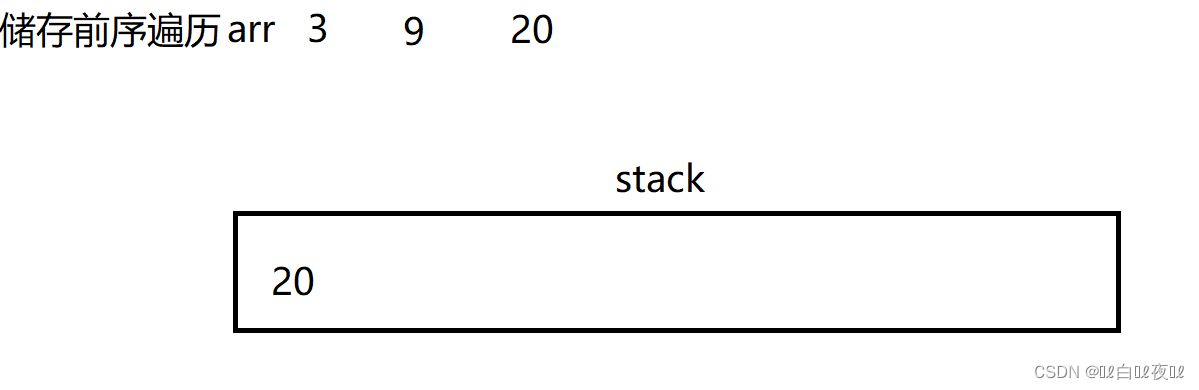
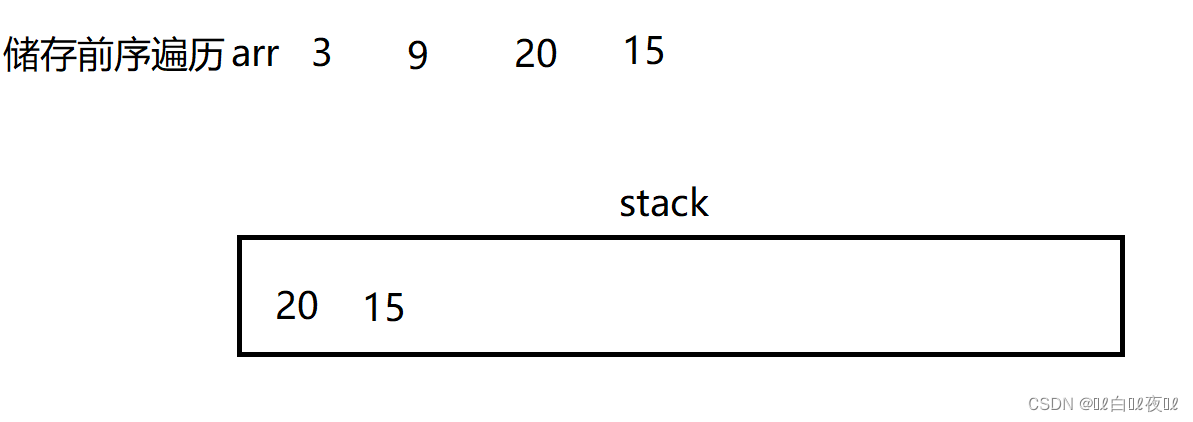
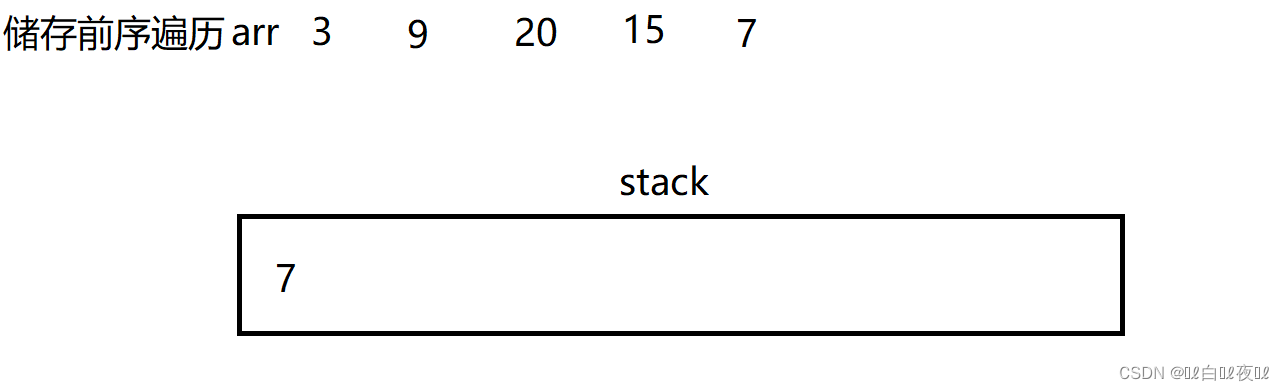
不停的去访问左子树，到空就取栈顶然后pop掉，让结点指针指向栈顶结点的右子树就可以了，以此循环。
代码：

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int>arr;//储存前序遍历的结果
        stack<TreeNode*>st;
        TreeNode* cur = root;
        while(!st.empty() || cur)//如果栈为空，并且cur指向了空，因为栈为空，cur指向的右子树说不定还有值
        {
            while(cur)
            {
                arr.push_back(cur->val);//将结点值添加到arr中
                st.push(cur);//入栈
                cur = cur->left;
            }
            TreeNode* top = st.top();//取栈顶结点
            st.pop();//出栈
            cur = top->right;//访问栈顶元素的右子树
        }
        return arr;
    }
};

94. 二叉树的中序遍历

给定一个二叉树的根节点 root ，返回它的中序遍历。
示例 1：

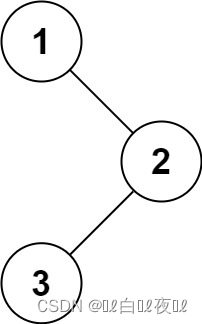
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶:

递归算法很简单，你可以通过迭代算法完成吗？

原题链接：https://leetcode.cn/problems/binary-tree-inorder-traversal/

思路：
中序遍历和前序遍历没什么太大差别，只是插入数据的位置不同而已，要在出栈的时候访问栈顶的元素。

代码：

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int>arr;//储存中序遍历的结果
        stack<TreeNode*>st;
        TreeNode* cur = root;
        while(!st.empty() || cur)
        {
            while(cur)
            {
                st.push(cur);//入栈
                cur = cur->left;
            }
            TreeNode* top = st.top();//取栈顶结点
            arr.push_back(top->val);//将结点值添加到arr中
            st.pop();//出栈
            cur = top->right;//访问栈顶元素的右子树
        }
        return arr;
    }
};

145. 二叉树的后序遍历

给你一棵二叉树的根节点 root ，返回其节点值的后序遍历。
示例 1：

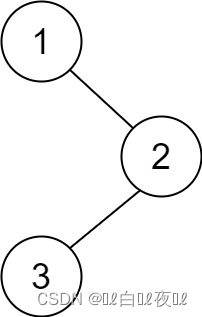
输入：root = [1,null,2,3]
输出：[3,2,1]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

树中节点的数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶：

递归算法很简单，你可以通过迭代算法完成吗？

原题链接：https://leetcode.cn/problems/binary-tree-postorder-traversal/

思路：
利用栈的基本思路是不变的，在弹出的时候，加一个判断条件，判断该节点的左子树和右子树是否全都访问完毕，如果访问完毕才能放进数组中。
这里只需要加一个结点指针指向栈最后一个弹出的结点就可以了：

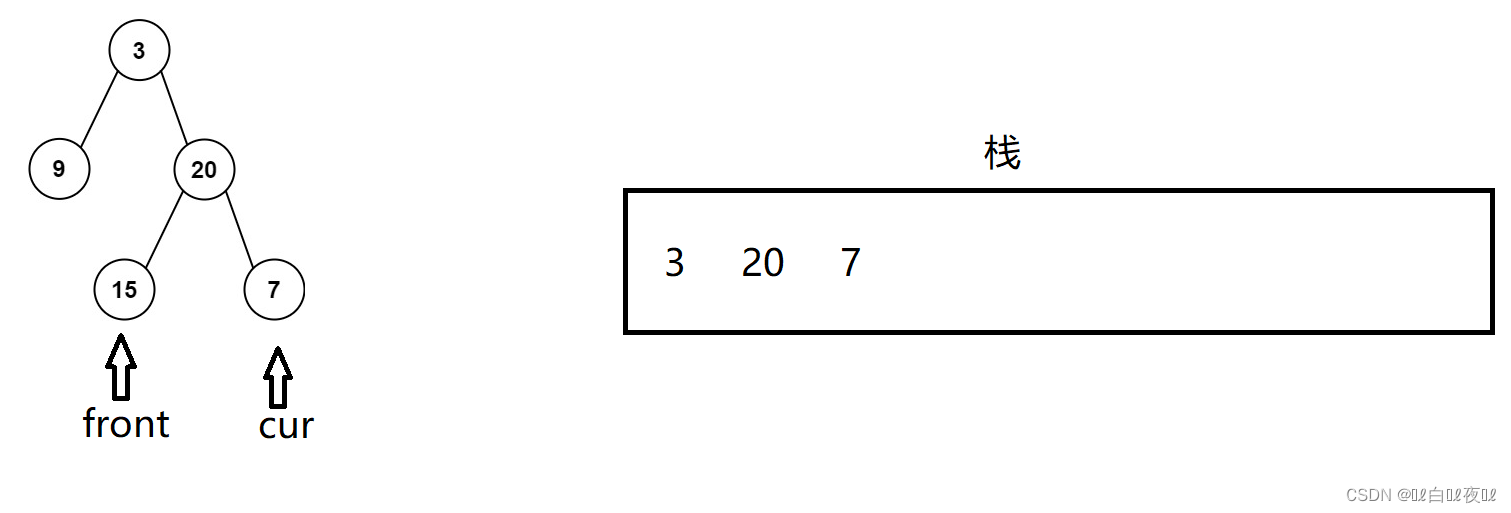
这里15结点已经从栈中弹出去了，然后是7也弹出去。
front就会指向cur的位置：

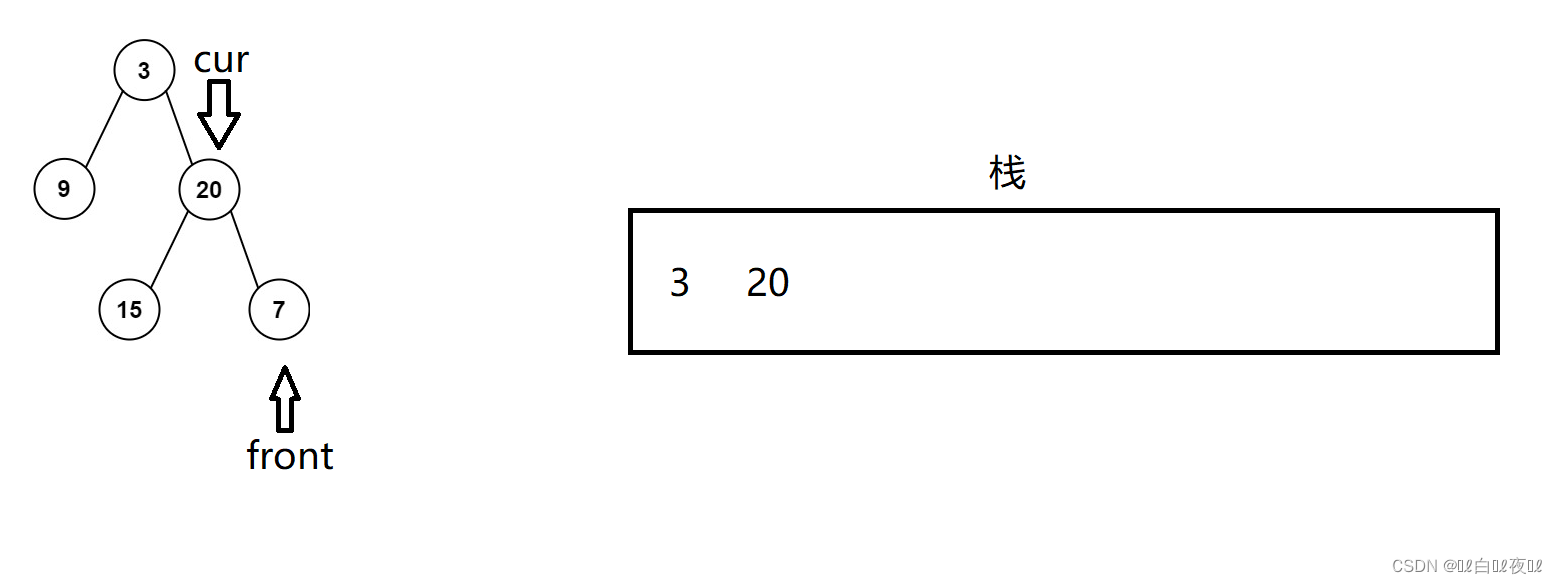
这个时候cur检测右子树是不是front就能知道右子树是不是已经被访问完毕了。

代码：

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int>arr;//储存后序遍历的结果
        stack<TreeNode*>st;
        TreeNode* cur = root;
        TreeNode* front = nullptr;//记录最后上一个出栈的结点位置
        while(cur || !st.empty())
        {
            while(cur)
            {
                st.push(cur);
                cur = cur -> left;
            }
            TreeNode* top = st.top();
            //如果栈顶节点右子树为空就说明该节点的左右子树都访问完毕了。
            //如果栈顶节点的右子树等于上个弹出的结点，那么也说明这该节点左右子树都访问完毕了。
            if(top->right == nullptr || top->right == front)
            {
                st.pop();
                arr.push_back(top->val);
                front = top;
            }
            else
            {
                cur = top -> right;
            }
        }
        return arr;
    }
};