文章目录
- 前言
- 一、预测建模
- 1.1 预测建模涉及的方面:
- 1.2 预测建模的几何理解
- 1.3 预测模型参数估计的基本策略
- 1.4 有监督学习算法与损失函数:
- 1.5 参数解空间和搜索策略
- 1.6 预测模型的评价
- 1.6.1 模型误差的评价指标
- 1.6.2 模型的图形化评价工具
- 1.6.3 训练误差和泛化误差
- 1.6.4 数据集的划分策略
- 二、预测模型的选择问题
- 2.1 预测模型的偏差和方差
- 三、综合应用:空气污染的分类预测
- 总结
前言
数据预测,简而言之就是基于已有数据集,归纳出输入变量和输出变量之间的数量关系。基于这种数量关系:
- 一方面,可发现对输出变量产生重要影响的输入变量;
- 另一方面,在数量关系具有普适性和未来不变的假设下,可用于对新数据输出变量取值的预测。
- 对数值型输出变量的预测称为回归。对分类型输出变量的预测称为分类
数据预测涉及的问题:
- 第一,预测建模
- 第二,模型评价
- 第三,模型选择
一、预测建模
1.1 预测建模涉及的方面:
- 第一,预测模型的形式
- 第二,预测模型的几何意义
- 第三,模型参数的估计
什么是预测模型?
- 预测模型一般以数学形式展现,以精确刻画和表述输入变量和输出变量取值之间的数量关系。可细分为回归预测模型和分类预测模型,分别适用于回归问题和分类问题
- 回归预测模型:
y = β 0 + β 1 X 1 + β 2 X 2 + . . . + β p X p + ε y = β_0+β_1X_1+β_2X_2+...+β_pX_p+\varepsilon y=β0+β1X1+β2X2+...+βpXp+ε - 分类预测模型:
l o g ( P 1 − P ) = β 0 + β 1 X 1 + β 2 X 2 + . . . + β p X p + ε log(\frac{P}{1-P})=β_0+β_1X_1+β_2X_2+...+β_pX_p+\varepsilon log(1−PP)=β0+β1X1+β2X2+...+βpXp+ε - 用于预测的回归方程:
y ^ = β 0 ^ + β 1 ^ X 1 + β 2 ^ X 2 + . . . + β p ^ X p \hat{y}=\hat{β_0}+\hat{β_1}X_1+\hat{β_2}X_2+...+\hat{β_p}X_p y^=β0^+β1^X1+β2^X2+...+βp^Xp
L o g i t P ^ = l o g ( P ^ 1 − P ^ ) = β 0 ^ + β 1 ^ X 1 + β 2 ^ X 2 + . . . + β p ^ X p Logit\hat{P}=log(\frac{\hat{P}}{1-\hat{P}})=\hat{β_0}+\hat{β_1}X_1+\hat{β_2}X_2+...+\hat{β_p}X_p LogitP^=log(1−P^P^)=β0^+β1^X1+β2^X2+...+βp^Xp
预测模型的其他形式:
- 推理规则:以逻辑判断的形式反映输入变量和输出变量之间的取值规律
- 推理规则集和图形化表示

1.2 预测建模的几何理解
-
预测建模的出发点,是将数据集中的N个样本观测数据,视为 p p p维实数空间 R p R^p Rp中的 N N N个点
-
回归预测模型::
- 回归直线
- 回归平面
-
分类预测模型:
- 分类直线
- 分类平面
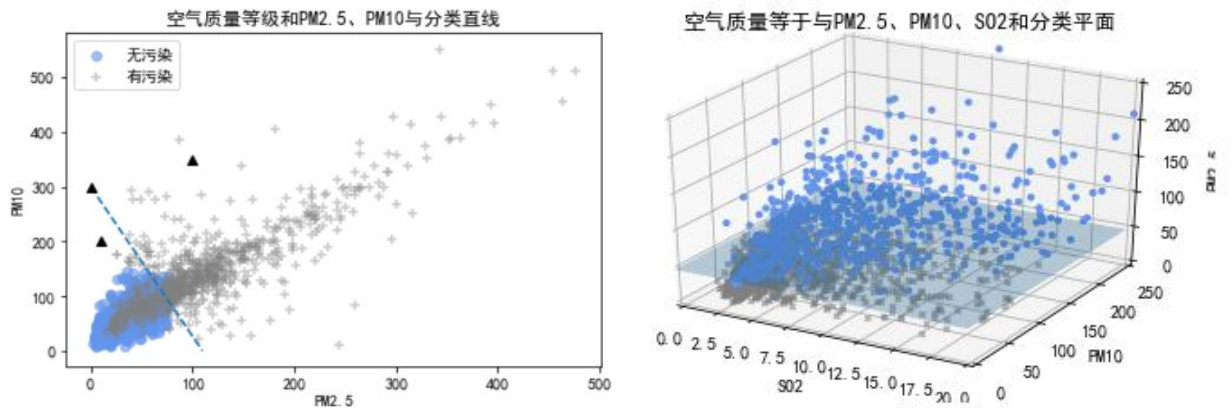
-
从直线到曲线,从平面到曲面

1.3 预测模型参数估计的基本策略
- 第一,预测建模参数估计以损失函数最小为目标,通常采用有监督学习算法。
- 第二,预测建模的参数估计通常借助特定的搜索策略进行。
1.4 有监督学习算法与损失函数:
损失函数L是误差e的函数
-
回归预测中的平方损失函数:
L ( e ) = L ( y i , y i ^ ) = ( y i − y i ^ ) 2 L(e)=L(y_i,\hat{y_i})=(y_i-\hat{y_i})^2 L(e)=L(yi,yi^)=(yi−yi^)2
∑ i = 1 N L ( y i , y i ^ ) = ∑ i = 1 N ( y i − y i ^ ) 2 \displaystyle \sum^{N}_{i=1}L(y_i,\hat{y_i})=\displaystyle \sum^{N}_{i=1}(y_i-\hat{y_i})^2 i=1∑NL(yi,yi^)=i=1∑N(yi−yi^)2 -
分类预测中的交互熵:
L ( y i , p k ^ ( X i ) ) = − ∑ k = 1 K I ( y i = k ) l o g ( P k ^ ( X i ) ) = − l o g P y i ^ ( X i ) L(y_i,\hat{p_k}(X_i))=-\displaystyle \sum^{K}_{k=1}I(y_i=k)log(\hat{P_k}(X_i))=-log\hat{P_{y_i}}(X_i) L(yi,pk^(Xi))=−k=1∑KI(yi=k)log(Pk^(Xi))=−logPyi^(Xi) -
二项偏差损失函数:
L ( y i , f ^ ( X i ) ) = − y i f ^ ( X i ) + l o g ( 1 + e x p ( f ^ ( X i ) ) ) L(y_i,\hat{f}(X_i))=-y_i\hat{f}(X_i)+log(1+exp(\hat{f}(X_i))) L(yi,f^(Xi))=−yif^(Xi)+log(1+exp(f^(Xi))) -
指数损失函数:
L ( y i , f ^ ( X i ) ) = e x p ( − y i f ^ ( X i ) ) L(y_i,\hat{f}(X_i))=exp(-y_i\hat{f}(X_i)) L(yi,f^(Xi))=exp(−yif^(Xi)) -
多分类下的损失函数:
L ( y i , f k ^ ( X i ) ) = − ∑ k = 1 K I ( y i = k ) l o g ( e x p ( f k ^ ( X i ) ) s u m l = 1 K e x p ( f l ^ ( X i ) ) ) L(y_i, \hat{f_k}(X_i))=-\displaystyle \sum^{K}_{k=1}I(y_i=k)log(\frac{exp(\hat{f_k}(X_i))}{\displaystyle sum^{K}_{l=1}exp(\hat{f_l}(X_i))}) L(yi,fk^(Xi))=−k=1∑KI(yi=k)log(suml=1Kexp(fl^(Xi))exp(fk^(Xi)))
1.5 参数解空间和搜索策略
- 参数的最小二乘估计:
∑ i = 1 N L ( y i , y i ^ ) = ∑ i = 1 N L ( y i , f ^ ( X i ) ) = ∑ i = 1 N ( y i − ( β 0 ^ + β 1 ^ X i 1 + β 2 ^ X i 2 + . . . + β p ^ X i p ) ) 2 \displaystyle \sum^{N}_{i=1}L(y_i,\hat{y_i})=\displaystyle \sum^{N}_{i=1} L(y_i,\hat{f}(X_i))=\displaystyle \sum^{N}_{i=1}(y_i-(\hat{\beta_0}+\hat{\beta_1}X_{i1}+\hat{\beta_2}X_{i2}+...+\hat{\beta_p}X_{ip}))^2 i=1∑NL(yi,yi^)=i=1∑NL(yi,f^(Xi))=i=1∑N(yi−(β0^+β1^Xi1+β2^Xi2+...+βp^Xip))2

-
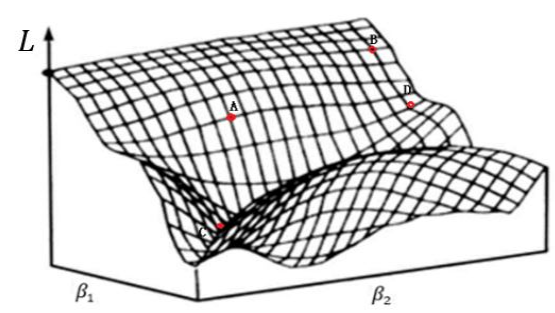
参数解空间和搜索策略:
- 在预测模型参数解空间中,采用一定的搜索策略估计参数

- 梯度下降法
1.6 预测模型的评价
- 两个重要概念
- 模型误差: 简称误差,是基于数据集,对模型预测值和实际值不一致程度的数值化度量。包括对每个样本观测的度量和对数据集整体的度量两个部分
- 预测误差或泛化误差: 是预测模型对新数据集进行预测时,给出的预测值和实际值不一致程度的数值化度量。预测误差测度模型在未来新数据集上的预测性能。若值较低,说明模型具有一般预测场景下的普适性和推广性,认为模型有较高的泛化能力
-
讨论的问题:
- 第一,模型误差的评价指标
- 第二,模型的图形化评价工具
- 第三,泛化误差的估计方法
1.6.1 模型误差的评价指标
(1)回归预测模型中的误差评价指标:均方误差(MSE)
M
S
E
=
1
N
∑
i
=
1
N
(
y
i
−
y
i
^
)
2
=
E
(
L
(
y
i
,
f
^
(
X
i
)
)
)
MSE=\frac{1}{N}\displaystyle \sum^{N}_{i=1}(y_i-\hat{y_i})^2=E(L(y_i,\hat{f}(X_i)))
MSE=N1i=1∑N(yi−yi^)2=E(L(yi,f^(Xi)))
(2)二分类预测模型中的误差评价指标

- 查准率(Precision):
P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} Precision=TP+FPTP - 查全率(Recall):
R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP - 准确率(Accuracy):
A c c u r a c y = T P + T N 样本总数 Accuracy = \frac{TP+TN}{样本总数} Accuracy=样本总数TP+TN - F1分数:
F 1 s c o r e = 2 × P × R P + R = 2 × T P N + T P − T N F1score=\frac{2\times P \times R}{P+R}=\frac{2\times TP}{N+TP-TN} F1score=P+R2×P×R=N+TP−TN2×TP - 真正率\灵敏度(TPR):
T P R = T P T P + F N TPR=\frac{TP}{TP+FN} TPR=TP+FNTP - 假正率\特异性(FPR):
F P R = T N T N + F P FPR=\frac{TN}{TN+FP} FPR=TN+FPTN
解释说明:
- TP:被模型预测为正类的正样本
- TN:被模型预测为负类的负样本
- FP:被模型预测为正类的负样本
- FN:被模型预测为负类的正样本
通俗理解
以西瓜数据集为例,我们来通俗理解一下什么是TP、TN、FP、FN。
- TP:被模型预测为好瓜的好瓜(是真正的好瓜,而且也被模型预测为好瓜)
- TN:被模型预测为坏瓜的坏瓜(是真正的坏瓜,而且也被模型预测为坏瓜)
- FP:被模型预测为好瓜的坏瓜(瓜是真正的坏瓜,但是被模型预测为了好瓜)
- FN:被模型预测为坏瓜的好瓜(瓜是真正的好瓜,但是被模型预测为了坏瓜)
(3)多分类预测模型中的误差评价指标:
- 微平均(Micro-averaged)意义下的评价指标;
- 宏平均(Macro-averaged)意义下的评价指标(如宏F1-分数)
1.6.2 模型的图形化评价工具
- ROC曲线和AUG值
- P-R曲线
# 代码实现ROC曲线和P-R曲线
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
#指定默认字体
plt.rcParams['font.sans-serif']=['FZHuaLi-M14S']
plt.rcParams['axes.unicode_minus'] = False
data = pd.read_csv('类别和概率.csv')
label=data['label']
prob=data['prob']
pos = np.sum(label == 1)
neg = np.sum(label == 0)
prob_sort = np.sort(prob)[::-1]
index = np.argsort(prob)[::-1]
label_sort = label[index]
Pre = []
Rec = []
tpr=[]
fpr=[]
for i, item in enumerate(prob_sort):
Rec.append(np.sum((label_sort[:(i+1)] == 1)) /pos)
Pre.append(np.sum((label_sort[:(i+1)] == 1))/(i+1))
tpr.append(np.sum((label_sort[:(i+1)] == 1))/pos)
fpr.append(np.sum((label_sort[:(i+1)] == 0)) /neg)
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,4))
axes[0].plot(fpr,tpr,'k')
axes[0].set_title('ROC曲线')
axes[0].set_xlabel('FPR')
axes[0].set_ylabel('TPR')
axes[0].plot([0, 1], [0, 1], 'r--')
axes[0].set_xlim([-0.01, 1.01])
axes[0].set_ylim([-0.01, 1.01])
axes[1].plot(Rec,Pre,'k')
axes[1].set_title('P-R曲线')
axes[1].set_xlabel('查全率R')
axes[1].set_ylabel('查准率P')
axes[1].plot([0,1],[1,pos/(pos+neg)], 'r--')
axes[1].set_xlim([-0.01, 1.01])
axes[1].set_ylim([pos/(pos+neg)-0.01, 1.01])
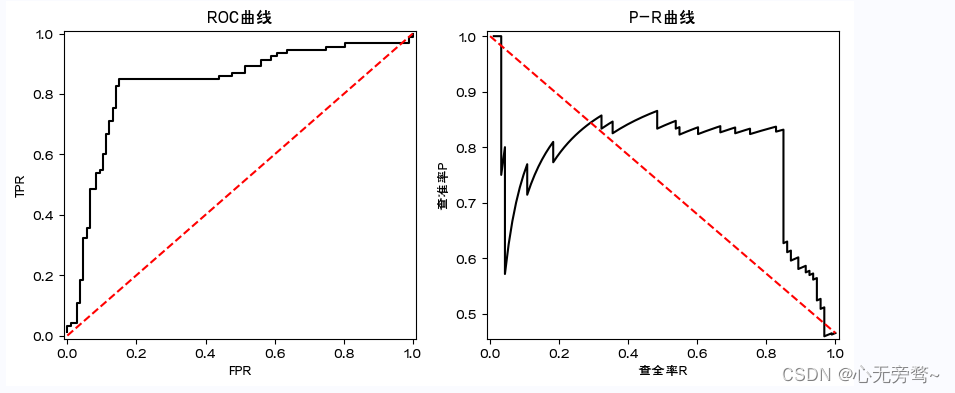
-
ROC曲线
在模型预测的时候,我们输出的预测结果是一堆[0,1]之间的数值,怎么把数值变成二分类?设置一个阈值,大于这个阈值的值分类为1,小于这个阈值的值分类为0。ROC曲线就是我们从[0,1]设置一堆阈值,每个阈值得到一个(TPR,FPR)对,纵轴为TPR,横轴为FPR,把所有的(TPR,FPR)对连起来就得到了ROC曲线。 -
PR曲线
同理ROC曲线。在模型预测的时候,我们输出的预测结果是一堆[0,1]之间的数值,怎么把数值变成二分类?设置一个阈值,大于这个阈值的值分类为1,小于这个阈值的值分类为0。ROC曲线就是我们从[0,1]设置一堆阈值,每个阈值得到一个(Precision,Recall)对,纵轴为Precision,横轴为Recall,把所有的(Precision,Recall)对对连起来就得到了PR曲线。
注意:AUC即为ROC曲线下的面积,而P-R曲线下的面积为AP值。mAP是多个类别AP的平均值,这个mean的意思是对每个类的AP再求平均,得到的就是mAP的值,mAP的大小一定在[0,1]区间,越大越好。该指标是目标检测算法中最重要的一个。
1.6.3 训练误差和泛化误差
-
训练误差:用于训练模型的数据集称为训练集,其中的样本观测为“袋内观测”。基于
训练集“袋内观测”,建立模型并计算得到的模型误差,称为训练误差或经验误差。
e r r ‾ = E ( L ( y i , f ^ ( X i ) ) ) = 1 N t r a i n i n g ∑ i = 1 N t r a i n i n g ( y i − y i ^ ) 2 \overline{err}=E(L(y_i, \hat{f}(X_i)))=\frac{1}{N_{training}}\displaystyle \sum^{N_{training}}_{i=1}(y_i-\hat{y_i})^2 err=E(L(yi,f^(Xi)))=Ntraining1i=1∑Ntraining(yi−yi^)2 -
训练误差的大小与模型复杂度和训练样本量有关

-
训练样本量和训练误差的理论关系

-
泛化误差的估计:泛化误差是无法直接计算的
-
泛化误差是基于“袋外观测”(OOB)的误差,而非训练误差
-
损失函数最小原则下的模型参数估计策略决定了:训练误差是基于“袋内观测”的当下最小值,对基于OOB误差来讲,它是个偏低的估计
-
预测建模时通常只抽取数据集中的部分样本观测组成训练集(这里记为 Τ )并训练模型。剩余的样本观测全体称为测试集。评价模型时将计算模型在测试集上的误差,该误差称为测试误差。因测试误差基于OOB计算,通常作为模型泛化误差的估计
E r r T = E [ L ( y i , h a t f ( X i ) ) ∣ T ] = 1 N t e s t ∑ i = 1 N t e s t ( y i − y i ^ ) 2 E r r = E [ L ( y i , f ^ ( X i ) ) ] = E [ E r r T ] Err_T=E[L(y_i,hat{f}(X_i))|T]=\frac{1}{N_{test}}\displaystyle \sum^{N_{test}}_{i=1}(y_i-\hat{y_i})^2 \\\ Err=E[L(y_i, \hat{f}(X_i))]=E[Err_T] ErrT=E[L(yi,hatf(Xi))∣T]=Ntest1i=1∑Ntest(yi−yi^)2 Err=E[L(yi,f^(Xi))]=E[ErrT] -
Err是对随机样本所有可能下的测试误差的平均,包括了训练集T随机变化导致的 f ^ \hat{f} f^的变化,Err是对一类预测模型 f f f泛化误差的理论估计
-
-
训练误差和测试误差的关系(单次随机划分和多次随机划分的情况)

- 训练误差和测试误差关系总结:
- 第一,训练误差是对泛化误差的偏低估计,应采用测试误差估计泛化误差。
- 第二,训练误差最小时候的测试误差不一定最小,也即训练误差最小下的预测模型,其泛化能力不一定最强。
- 第三,理想的预测模型应是泛化能力最强的模型,是测试误差最小下的模型。

代码实现如下:
# 导入所需模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
# 解决中文乱码问题
plt.rcParams['font.sans-serif']=['FZHuaLi-M14S']
plt.rcParams['axes.unicode_minus'] = False
import warnings
warnings.filterwarnings(action = 'ignore')
from sklearn.metrics import confusion_matrix,f1_score,roc_curve, auc, precision_recall_curve,accuracy_score
from sklearn.model_selection import train_test_split,KFold,LeaveOneOut,LeavePOut # 数据集划分方法
from sklearn.model_selection import cross_val_score,cross_validate # 计算交叉验证下的测试误差
from sklearn import preprocessing
import sklearn.linear_model as LM
from sklearn import neighbors
# 训练误差的大小与模型复杂度和训练样本量的关系图像
np.random.seed(123)
N=200
x=np.linspace(0.1,10, num=N)
y=[]
z=[]
for i in range(N):
tmp=10*np.math.sin(4*x[i])+10*x[i]+20*np.math.log(x[i])+30*np.math.cos(x[i])
y.append(tmp)
tmp=y[i]+np.random.normal(0,3)
z.append(tmp)
fig,axes=plt.subplots(nrows=1,ncols=3,figsize=(15,4))
axes[0].scatter(x,z,s=5)
axes[0].plot(x,y,'k-',label="真实关系")
modelLR=LM.LinearRegression()
X=x.reshape(N,1)
Y=np.array(z)
modelLR.fit(X,Y)
axes[0].plot(x,modelLR.predict(X),label="线性模型")
linestyle=['--','-.',':','-']
for i in np.arange(1,5):
tmp=pow(x,(i+1)).reshape(N,1)
X=np.hstack((X,tmp))
modelLR.fit(X,Y)
axes[0].plot(x,modelLR.predict(X),linestyle=linestyle[i-1],label=str(i+1)+"项式")
axes[0].legend()
axes[0].set_title("真实关系和不同复杂度模型的拟合情况")
axes[0].set_xlabel("输入变量")
axes[0].set_ylabel("输出变量")
X=x.reshape(N,1)
Y=np.array(z)
modelLR.fit(X,Y)
MSEtrain=[np.sum((Y-modelLR.predict(X))**2)/(N-2)]
for i in np.arange(1,9):
tmp=pow(x,(i+1)).reshape(N,1)
X=np.hstack((X,tmp))
modelLR.fit(X,Y)
MSEtrain.append(np.sum((Y-modelLR.predict(X))**2)/(N-(i+2)))
axes[1].plot(np.arange(1,10),MSEtrain,marker='o',label='训练误差')
axes[1].legend()
axes[1].set_title("不同复杂度模型的训练误差")
axes[1].set_xlabel("模型复杂度")
axes[1].set_ylabel("MSE")
X=x.reshape(N,1)
Y=np.array(z)
for i in np.arange(1,5): #采用5项式模型
tmp=pow(x,(i+1)).reshape(N,1)
X=np.hstack((X,tmp))
np.random.seed(0)
size=np.linspace(0.2,0.99,100)
MSEtrain=[]
for i in range(len(size)):
Ntraining=int(N*size[i])
id=np.random.choice(N,Ntraining,replace=False)
X_train=X[id]
y_train=Y[id]
modelLR.fit(X_train,y_train)
MSEtrain.append(np.sum((y_train-modelLR.predict(X_train))**2)/(Ntraining-6))
tmpx=np.linspace(1,len(size), num=len(size)).reshape(len(size),1) #拟合MSE
tmpX=np.hstack((tmpx,tmpx**2))
tmpX=np.hstack((tmpX,tmpx**3))
modelLR.fit(tmpX,MSEtrain)
axes[2].plot(size,MSEtrain,linewidth=1.5,linestyle='-',label='MSE')
axes[2].plot(size,modelLR.predict(tmpX),linewidth=1.5,linestyle='--',label='MSE趋势线')
axes[2].set_title("训练样本量和训练MSE")
axes[2].set_xlabel("训练样本量水平")
axes[2].set_ylabel("MSE")
axes[2].legend()
plt.show()
结果如下:
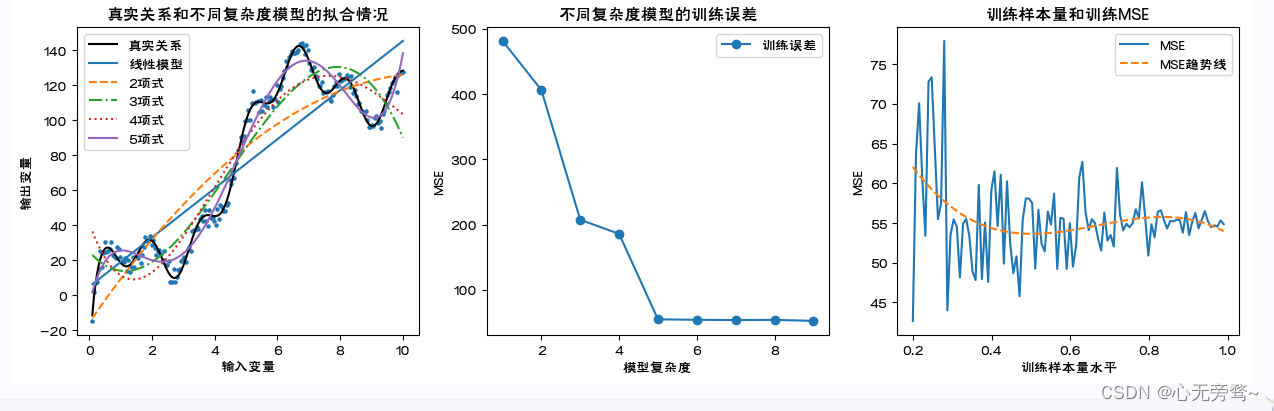
说明:
1、这里通过数据模拟直观展示模型复杂度和训练误差的关系。随模型复杂度的提高,训练误差单调下降。
2、首先设定输入变量和输出变量的真实关系,并通过加上服从正态分布的随机数模拟其他随机因素对输出变量的影响。这里,设定的真实关系函数可以被泰勒展开,因此一定是次数越高的多项式模型越贴近真实观测值。 到达一定阶数(这里为9)后继续增加阶数对参数估计结果的影响很小可以忽略,无需再增加阶数。
3、分别建立各个多项式模型。这里消除了模型复杂度本身导致对MSE计算结果的影响,MSE计算时分母为自由度:样本量-(输入变量个数+1)。
4、考察训练集样本量对对于特定模型(这里为五项式)学习充分性的影响。样本量依次为原数据集的20%至99%。这里消除了样本量本身对MSE计算结果的影响,MSE计算时分母为自由度:样本量-(输入变量个数+1)。对不同样本量下的MSE进行三次曲线拟合。
# 训练误差和测试误差的关系图像
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,4))
modelLR=LM.LinearRegression()
np.random.seed(123)
Ntraining=int(N*0.7)
Ntest=int(N*0.3)
id=np.random.choice(N,Ntraining,replace=False)
X_train=x[id].reshape(Ntraining,1)
y_train=np.array(z)[id].reshape(Ntraining,1)
modelLR.fit(X_train,y_train)
MSEtrain=[np.sum((y_train-modelLR.predict(X_train))**2)/(Ntraining-2)]
xtest= np.delete(x, id).reshape(Ntest,1)
X_test= np.delete(x, id).reshape(Ntest,1)
y_test=np.delete(z,id).reshape(Ntest,1)
MSEtest=[np.sum((y_test-modelLR.predict(X_test))**2)/(Ntest-2)]
for i in np.arange(1,9):
tmp=pow(x[id],(i+1)).reshape(Ntraining,1)
X_train=np.hstack((X_train,tmp))
modelLR.fit(X_train,y_train)
MSEtrain.append(np.sum((y_train-modelLR.predict(X_train))**2)/(Ntraining-(i+2)))
tmp=pow(xtest,(i+1)).reshape(Ntest,1)
X_test=np.hstack((X_test,tmp))
MSEtest.append(np.sum((y_test-modelLR.predict(X_test))**2)/(Ntest-(i+2)))
axes[0].plot(np.arange(1,10,1),MSEtrain,marker='o',label='训练误差')
axes[0].plot(np.arange(1,10,1),MSEtest,marker='*',label='测试误差')
axes[0].legend()
axes[0].set_title("不同复杂度模型的训练误差和测试误差")
axes[0].set_xlabel("模型复杂度")
axes[0].set_ylabel("MSE")
MSEtrain=[]
MSEtest=[]
for j in range(20):
x=np.linspace(0.1,10, num=N)
id=np.random.choice(N,Ntraining,replace=False)
X_train=x[id].reshape(Ntraining,1)
y_train=np.array(z)[id].reshape(Ntraining,1)
modelLR.fit(X_train,y_train)
mse_train=[np.sum((y_train-modelLR.predict(X_train))**2)/(Ntraining-2)]
xtest= np.delete(x, id).reshape(Ntest,1)
X_test= np.delete(x, id).reshape(Ntest,1)
y_test=np.delete(z,id).reshape(Ntest,1)
mse_test=[np.sum((y_test-modelLR.predict(X_test))**2)/(Ntest-2)]
for i in np.arange(1,9):
tmp=pow(x[id],(i+1)).reshape(Ntraining,1)
X_train=np.hstack((X_train,tmp))
modelLR.fit(X_train,y_train)
mse_train.append(np.sum((y_train-modelLR.predict(X_train))**2)/(Ntraining-(i+2)))
tmp=pow(xtest,(i+1)).reshape(Ntest,1)
X_test=np.hstack((X_test,tmp))
mse_test.append(np.sum((y_test-modelLR.predict(X_test))**2)/(Ntest-(i+2)))
plt.plot(np.arange(1,10),mse_train,marker='o',linewidth=0.8,c='lightcoral',linestyle='-')
plt.plot(np.arange(1,10),mse_test,marker='*',linewidth=0.8,c='lightsteelblue',linestyle='-.')
MSEtrain.append(mse_train)
MSEtest.append(mse_test)
MSETrain=pd.DataFrame(MSEtrain)
MSETest=pd.DataFrame(MSEtest)
axes[1].plot(np.arange(1,10),MSETrain.mean(),marker='o',linewidth=1.5,c='red',linestyle='-',label="训练误差的期望")
axes[1].plot(np.arange(1,10),MSETest.mean(),marker='*',linewidth=1.5,c='blue',linestyle='-',label="测试误差的期望")
axes[1].set_title("不同复杂度模型的训练误差和测试误差及其期望")
axes[1].set_xlabel("模型复杂度")
axes[1].set_ylabel("MSE")
axes[1].legend()
plt.show()
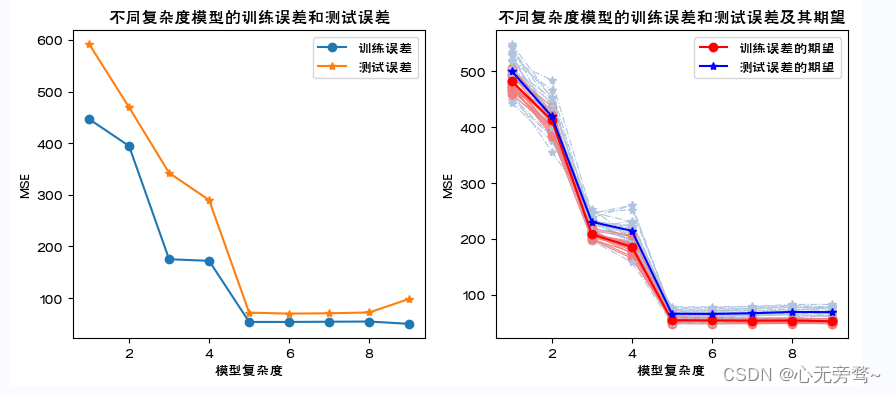
说明:
1、这里通过数据模拟直观展示不同复杂度模型下训练误差和测试误差的关系。随模型复杂度的提高,训练误差单调下降,测试误差呈先下降后来上升的U字形。
2、从数据集中随机抽取一定比例的样本观测组成训练集训练模型,剩余的样本观测组成测试集计算测试误差。这里进行了20次。
3、样本观测的随机抽取必然导致20个训练集包含可能不同的样本观测,由此模型的参数估计值会有差别,从而使得20个训练误差和测试误差的数值结果不尽相等。带圆点的浅红色和浅灰色分别对应20次抽样的训练误差和测试误差,它们各自的均值对应带星号的红色和蓝色线。
1.6.4 数据集的划分策略
-
训练误差可表述为:
C V ( f ^ , α ) = 1 N ∑ i = 1 N L ( y i , f ^ − k ( i ) ( X i , α ) ) CV(\hat{f}, \alpha)=\frac{1}{N}\displaystyle \sum^{N}_{i=1}L(y_i,\hat{f}^{-k(i)}(X_i,\alpha)) CV(f^,α)=N1i=1∑NL(yi,f^−k(i)(Xi,α))- α \alpha α表示人为指定的数据集划分策略。 α \alpha α不同所导致的训练集不同将最终体现在预测模型上,因此将预测模型记为: f ^ − k ( X , α ) \hat{f}^{-k}(X,\alpha) f^−k(X,α),表示第 α \alpha α个预测模型(基于删去 k k k部分数据之外的数据)
-
数据集的划分:
- 旁置法(Hold out)
- 留一法(Leave One Out, LOO)
- K折交叉验证法(K Cross-validation,CV)
-
旁置法
旁置法,将整个样本集随机划分为两个集合。一个集合称为训练样本集,通常包含60%至70% 的观测,用于训练预测模型。另一个集合称为测试样本集,用于估计预测误差。即利用建立在训练样本集上的预测模型对测试样本集做预测并计算其预测误差。该预测误差也称为测试误差,将作为模型预测误差的估计。

- 留一法
用 N - 1 N-1 N-1个样本观测作为训练集训练模型,用剩余的一个样本观测作为测试集计算模型的测试误差
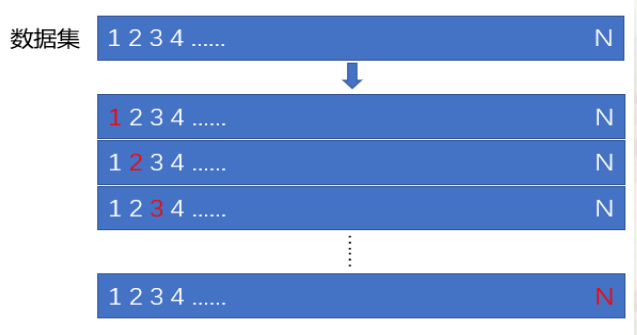
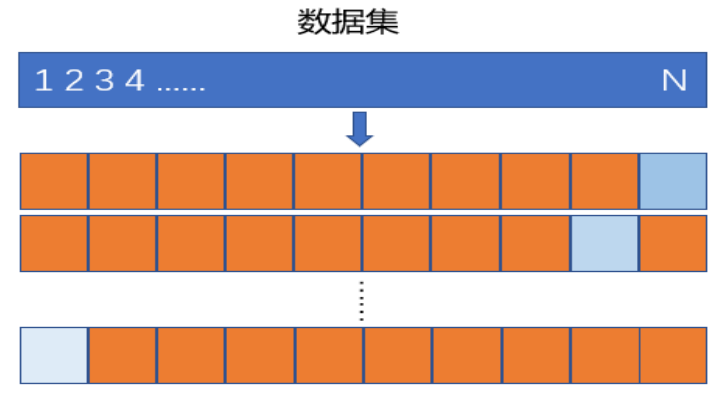
- K折交叉验证
首先将数据集随机近似等分为不相交的 K K K份,称为 K K K折;然后,令其中的 K - 1 K-1 K-1份为训练集训练模型,剩余的1份为测试集计算测试误差
# 旁置法和留一法
np.random.seed(123)
N=200
x=np.linspace(0.1,10, num=N)
y=[]
z=[]
for i in range(N):
tmp=10*np.math.sin(4*x[i])+10*x[i]+20*np.math.log(x[i])+30*np.math.cos(x[i])
y.append(tmp)
tmp=y[i]+np.random.normal(0,3)
z.append(tmp)
X=x.reshape(N,1)
Y=np.array(z)
for i in np.arange(1,5): #采用5项式模型
tmp=pow(x,(i+1)).reshape(N,1)
X=np.hstack((X,tmp))
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,train_size=0.70, random_state=123) #旁置法
print("旁置法的训练集:%s ;测试集:%s" % (X_train.shape,X_test.shape))
loo = LeaveOneOut() #留一法
for train_index, test_index in loo.split(X):
print("留一法训练集的样本量:%s;测试集的样本量: %s" % (len(train_index), len(test_index)))
break
lpo = LeavePOut(p=3) # 留p法
for train_index, test_index in lpo.split(X):
print("留p法训练集的样本量:%s;测试集的样本量: %s" % (len(train_index),len(test_index)))
break
kf = KFold(n_splits=5,shuffle=True,random_state=123) # K折交叉验证法
for train_index, test_index in kf.split(X): #给出索引
print("5折交叉验证法的训练集:",train_index,"\n测试集:",test_index)
break
# 结果如下:
旁置法的训练集:(140, 5) ;测试集:(60, 5)
留一法训练集的样本量:199;测试集的样本量: 1
留p法训练集的样本量:197;测试集的样本量: 3
5折交叉验证法的训练集: [ 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 16 17 18
21 22 23 24 25 27 28 29 30 32 33 34 35 36 38 39 40 41
42 43 44 45 46 47 48 49 51 54 55 56 57 58 59 60 61 62
63 64 65 66 67 68 69 70 71 73 74 75 76 77 78 80 81 83
84 86 87 89 90 91 92 94 96 97 98 99 100 101 102 103 105 106
107 109 110 111 112 113 114 115 116 117 118 120 122 123 124 125 126 129
130 131 132 134 135 136 137 138 141 142 143 145 146 147 148 150 151 152
153 154 155 156 157 159 160 161 163 164 165 167 168 169 171 173 174 175
176 177 181 186 187 188 190 191 192 193 194 195 196 197 198 199]
测试集: [ 4 19 20 26 31 37 50 52 53 72 79 82 85 88 93 95 104 108
119 121 127 128 133 139 140 144 149 158 162 166 170 172 178 179 180 182
183 184 185 189]
说明:
1、这里利用前述模拟数据,考察三种数据集划分及其测试误差的计算结果。需要引用sklearn.model_selection中的相关函数。
2、train_test_split(X,Y,train_size=0.70, random_state=123)实现数据集(X为输入变量矩阵,包含5个输入变量。输出变量为Y)划分的旁置法,这里指定训练集占原数据集(样本量为200)的70%,剩余30%为测试集。可指定random_state为任意整数以确保数据集的随机划分结果可以重现。函数依次返回训练集和测试集的输入变量和输出变量。可以看到划分结果为:训练集:(140, 5) ;测试集:(60, 5)。
3、LeaveOneOut()实现留一法,可利用结果对象的split方法,浏览数据集的划分结果,即训练集和测试集的样本观测索引(编号)。因原数据集样本量为200,留一法将做200次训练集和测试集的轮换,可利用循环浏览每次的划分结果。这里利用break跳出循环,只看第1次的划分结果。LeavePOut(p=3)是对留一法的拓展,为留p法。例如这里测试集的样本量为3。
4、KFold(n_splits=5,shuffle=True,random_state=123)实现K折交叉验证法,这里为k=5。指定shuffle=True表示将数据顺序随机打乱后再做K折划分。这里仅显示了1次划分的结果(样本观测索引)。
# K折交叉验证
modelLR=LM.LinearRegression()
k=10
CVscore=cross_val_score(modelLR,X,Y,cv=k,scoring='neg_mean_squared_error') #sklearn.metrics.SCORERS.keys()
print("k=10折交叉验证的MSE:",-1*CVscore.mean())
scores = cross_validate(modelLR,X,Y, scoring='neg_mean_squared_error',cv=k, return_train_score=True)
print("k=10折交叉验证的MSE:",-1*scores['test_score'].mean()) # scores为字典
#N折交叉验证:LOO
CVscore=cross_val_score(modelLR,X,Y,cv=N,scoring='neg_mean_squared_error')
print("LOO的MSE:",-1*CVscore.mean())
# 运行结果如下:
k=10折交叉验证的MSE: 103.51193551457445
k=10折交叉验证的MSE: 103.51193551457445
LOO的MSE: 56.84058776221936
说明:cross_val_score()和cross_validate()都可自动给出模型在K折交叉验证法下的测试误差,cross_validate还可给出训练误差。这里,模型为一般线性回归模型(五项式模型),计算10折交叉验证法下的测试误差。参数scoring为模型预测精度的度量,指定特定字符串,计算相应评价指标的结果。例如:'neg_mean_squared_error’表示计算负的MSE。可通过sklearn.metrics.SCORERS.keys()浏览其他的评价指标。若指定参数cv等于样本量,可得到N折交叉验证法(即留一法LOO)下的测试误差。
二、预测模型的选择问题
-
模型选择的基本原则
- 预测模型选择的理论依据是“奥克姆剃刀(Occam‘s Razor)”原则
- 通常简单模型的训练误差高于复杂模型,但若其泛化误差低于复杂模型,则应选择简单模型
-
预测模型中的“佼佼者”应具有两个重要特征:
- 第一,训练误差在可接受的范围内
- 第二,具有一定的预测稳健性
-
选择复杂模型将导致怎样的后果?
- 第一,模型过拟合(Over-Fitting)而导致的高泛化误差
- 第二,模型过拟合而导致的低稳健性
-
模型过拟合
- 在以训练误差最小原则下可能出现的,预测模型远远偏离输入变量和输出变量的真实关系,从而在新数据集上有较大预测误差的现象
- 预测模型的训练误差较小但测试误差较大,是模型过拟和的重要表现之一
# 各种情况下的拟合
np.random.seed(123)
N=100
x=np.linspace(-10,10, num=N)
y=14+5.5*x+4.8*x**2+0.5*x**3
z=[]
for i in range(N):
z.append(y[i]+np.random.normal(0,50))
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,4))
axes[0].scatter(x,z,s=10)
axes[0].plot(x,y,'k-',label="真实关系")
modelLR=LM.LinearRegression()
X=x.reshape(N,1)
Y=np.array(z)
modelLR.fit(X,Y)
axes[0].plot(x,modelLR.predict(X),linestyle='--',label="线性模型")
linestyle=[':','-.']
degree=[2,3]
for i in range(len(degree)):
tmp=pow(x,degree[i]).reshape(N,1)
X=np.hstack((X,tmp))
modelLR.fit(X,Y)
axes[0].plot(x,modelLR.predict(X),linestyle=linestyle[i],label=str(degree[i])+"项式模型")
KNNregr=neighbors.KNeighborsRegressor(n_neighbors=5)
X=x.reshape(N,1)
KNNregr.fit(X,Y)
axes[0].plot(X,KNNregr.predict(X),linestyle='-',label="复杂模型")
axes[0].legend()
axes[0].set_title("真实关系和不同复杂度模型的拟合情况")
axes[0].set_xlabel("输入变量")
axes[0].set_ylabel("输出变量")
X=x.reshape(N,1)
Y=np.array(z)
modelLR.fit(X,Y)
np.random.seed(123)
k=10
scores = cross_validate(modelLR,X,Y, scoring='neg_mean_squared_error',cv=k, return_train_score=True)
MSEtrain=[-1*scores['train_score'].mean()]
MSEtest=[-1*scores['test_score'].mean()]
degree=[2,3]
for i in range(len(degree)):
tmp=pow(x,degree[i]).reshape(N,1)
X=np.hstack((X,tmp))
modelLR.fit(X,Y)
scores = cross_validate(modelLR,X,Y, scoring='neg_mean_squared_error',cv=k, return_train_score=True)
MSEtrain.append((-1*scores['train_score']).mean())
MSEtest.append((-1*scores['test_score']).mean())
KNNregr=neighbors.KNeighborsRegressor(n_neighbors=5)
X=x.reshape(N,1)
KNNregr.fit(X,Y)
scores = cross_validate(KNNregr,X,Y, scoring='neg_mean_squared_error',cv=k, return_train_score=True)
MSEtrain.append((-1*scores['train_score']).mean())
MSEtest.append((-1*scores['test_score']).mean())
axes[1].plot(np.arange(1,len(degree)+3),MSEtrain,marker='o',label='训练误差(10折交叉验证法)',linestyle='--')
axes[1].plot(np.arange(1,len(degree)+3),MSEtest,marker='*',label='测试误差(10折交叉验证法)')
axes[1].legend()
axes[1].set_title("不同复杂度模型的训练误差和测试误差(Err)")
axes[1].set_xlabel("模型复杂度")
axes[1].set_ylabel("MSE")
fig.show()
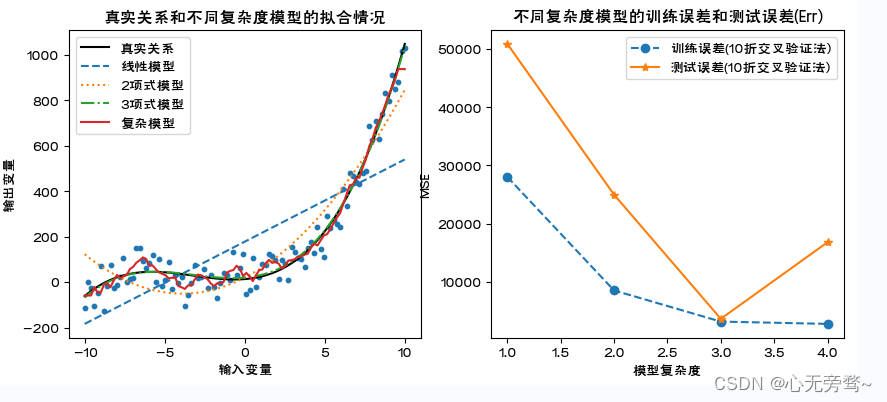
说明:
1、利用通过数据模拟,直观展示模型的过拟合,以及过拟合模型下的训练误差和测试误差的特点。
2、这里,复杂模型为K近邻法建立的预测模型,是一种典型的非线性模型。具体内容详见第4章。
3、对不同复杂度模型,利用cross_validate()计算10折交叉验证下的训练误差和测试误差。随模型复杂度的提高,训练误差单调下降,测试误差呈先下降后来上升的U字形。显然,复杂模型的训练误差最小但测试误差并非最小,出现了模型的过拟合。
4、scores[‘train_score’]为训练误差,scores[‘test_score’]为测试误差。
# 4个模型10折交叉验证下各折测试误差的分布特征
fig,axes = plt.subplots(1,2,figsize=(10,4))
modelLR=LM.LinearRegression()
X=x.reshape(N,1)
Y=np.array(z)
modelLR.fit(X,Y)
np.random.seed(123)
k=10
scores = cross_validate(modelLR,X,Y, scoring='neg_mean_squared_error',cv=k, return_train_score=True)
fdata=pd.Series(-1*scores['test_score'])
axes[0].boxplot(x=fdata,sym='rd',patch_artist=True,boxprops={'color':'blue','facecolor':'pink'},labels ={"线性模型"},showfliers=False)
MSEMedian=[np.median(-1*scores['test_score'])]
MSEVar=[(-1*scores['test_score']).var()]
MSEMean=[(-1*scores['test_score']).mean()]
degree=[2,3]
lab=['二项式模型','三项式项模型']
for i in range(len(degree)):
tmp=pow(x,degree[i]).reshape(N,1)
X=np.hstack((X,tmp))
modelLR.fit(X,Y)
scores = cross_validate(modelLR,X,Y, scoring='neg_mean_squared_error',cv=k, return_train_score=True)
fdata=pd.Series(-1*scores['test_score'])
axes[0].boxplot(x=fdata,sym='rd',positions=[i+2],patch_artist=True,boxprops={'color':'blue','facecolor':'pink'},labels ={lab[i]},
showfliers=False)
MSEMedian.append(np.median(-1*scores['test_score']))
MSEVar.append((-1*scores['test_score']).var())
MSEMean.append((-1*scores['test_score']).mean())
KNNregr=neighbors.KNeighborsRegressor(n_neighbors=5)
X=x.reshape(N,1)
KNNregr.fit(X,Y)
scores = cross_validate(KNNregr,X,Y, scoring='neg_mean_squared_error',cv=k, return_train_score=True)
fdata=pd.Series(-1*scores['test_score'])
axes[0].boxplot(x=fdata,sym='rd',positions=[4],patch_artist=True,boxprops={'color':'blue','facecolor':'pink'},labels ={"复杂模型"},
showfliers=False)
MSEMedian.append(np.median(-1*scores['test_score']))
MSEVar.append((-1*scores['test_score']).var())
MSEMean.append((-1*scores['test_score']).mean())
axes[0].plot(np.arange(1,5),MSEMedian,marker='o',linestyle='--')
axes[0].set_ylabel('MSE')
axes[0].set_xlabel('复杂度')
axes[0].set_title('不同复杂度模型下的Err(10折交叉验证法)')
axes[0].grid(linestyle="--", alpha=0.3)
axes[1].plot(np.arange(1,5),preprocessing.scale(MSEMean),marker='o',linestyle='-',label="Err")
axes[1].plot(np.arange(1,5),preprocessing.scale(MSEVar),marker='o',linestyle='--',label="方差")
axes[1].grid(linestyle="--", alpha=0.3)
axes[1].set_title('不同复杂度模型测试误差的期望(Err)与方差变化趋势图')
axes[1].set_xlabel('复杂度')
axes[1].set_ylabel('标准化值')
plt.legend(loc='best', bbox_to_anchor=(1, 1))
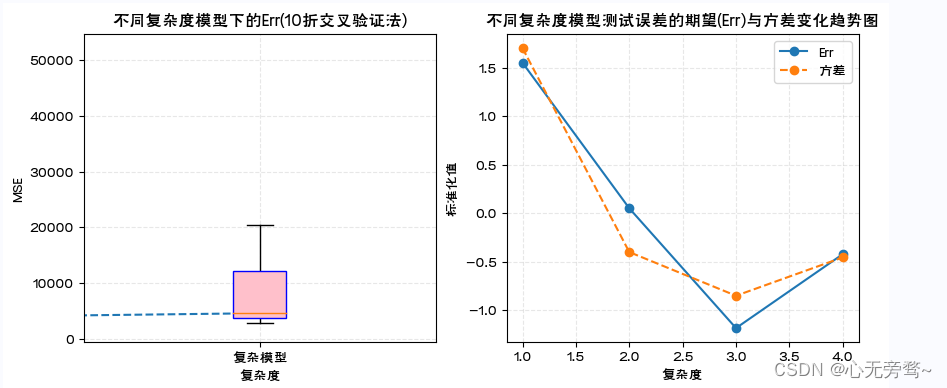
说明:
1、对于上述模拟数据和四种复杂度模型,利用箱线图展示了10折交叉验证下各折测试误差的统计分布。简单模型预测误差大,表现出测试误差箱线图的中位数线偏高,均值大,且箱体宽方差较大。随着复杂度增加情况相应发生改变。
2、boxplot()画箱线图时可以指定多个箱体在图中的位置(positions),箱体是否填充色(patch_artist=True),并以数据字典方式指定箱体边框颜色(‘color’:‘blue’)填充色(‘facecolor’:‘pink’),箱体标签(labels)以及是否显示数据中的异常点(showfliers)等。
3、preprocessing.scale()是对数据进行标准化处理,即数据减去均值除以标准差。处理后的数据均值等于0标准差等于1。通过标准化处理实现将不同数量级的数据变动趋势画在同一幅图中。
2.1 预测模型的偏差和方差
-
预测模型的偏差:
- 指对新数据集中的样本观测 X 0 X_0 X0(是模型的OOB观测),模型给出的多个预测值 y 0 i ^ \hat{y^{i}_0} y0i^(i=1,2,…)的期望 E ( y 0 i ^ ) E(\hat{y^{i}_0}) E(y0i^),与其实际值 y 0 y^0 y0的差,测度了预测值和实际值不一致程度的大小。
- 理论上,预测模型的偏差越小越好,表名模型的泛化误差小,泛化能力强。
-
预测模型的方差:
- 指对新数据集中的样本观测 X 0 X_0 X0,模型给出的多个预测值 y 0 i ^ \hat{y^{i}_0} y0i^的方差,测度了多个预测值波动程度的大小。
- 理论上,预测模型的方差越小越好,表明模型具有鲁棒性,泛化误差的估计可靠

-
预测模型的偏差-方差分解:
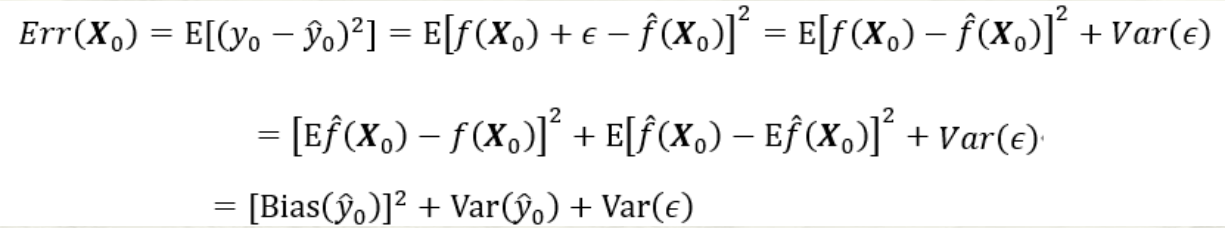
第三项为随机误差项的方差。无论怎样调整模型,第三项都不可能消失除非 σ ε 2 = 0 \sigma^{2}_{\varepsilon}=0 σε2=0;第一项为上述的偏差的平方,度量了预测值的平均值与真实值的差;第二项为上述的方差,度量了预测值与其期望间的平均性平方差异
- 预测模型的偏差和方差的关系:
模型复杂度增加带来 [ B i a s ( y 0 ^ ) ] 2 [Bias(\hat{y_0})]^2 [Bias(y0^)]2减少的同时,方差 V a r ( y 0 ^ ) Var(\hat{y_0}) Var(y0^)会随之增加。如果偏差的减少可以抵消方差的增加, E r r ( X 0 ) Err(X_0) Err(X0)会继续降低。但如果偏差的减少无法抵消方差的增加, E r r ( X 0 ) Err(X_0) Err(X0)则会增加。

# 预测模型的偏差和方差的变化趋势图
x0=np.array([x.mean(),x.mean()**2,x.mean()**3])
y0=14+5.5*x0[0]+4.8*x0[1]+0.5*x0[2]
X=x.reshape(N,1)
Y=np.array(z)
degree=[2,3]
for i in range(len(degree)):
tmp=pow(x,degree[i]).reshape(N,1)
X=np.hstack((X,tmp))
modelLR=LM.LinearRegression()
KNNregr=neighbors.KNeighborsRegressor(n_neighbors=5)
model1,model2,model3,model4=[],[],[],[]
kf = KFold(n_splits=10,shuffle=True,random_state=123)
for train_index, test_index in kf.split(X):
Ntrain=len(train_index)
XKtrain=X[train_index,]
YKtrain=Y[train_index,]
modelLR.fit(XKtrain[:,0].reshape(Ntrain,1),YKtrain)
model1.append(modelLR.predict(x0[0].reshape(1,1)))
modelLR.fit(XKtrain[:,0:2].reshape(Ntrain,2),YKtrain)
model2.append(modelLR.predict(x0[0:2].reshape(1,2)))
modelLR.fit(XKtrain[:,0:3].reshape(Ntrain,3),YKtrain)
model3.append(modelLR.predict(x0[0:3].reshape(1,3)))
KNNregr.fit(XKtrain[:,0].reshape(Ntrain,1),YKtrain)
model4.append(KNNregr.predict(x0[0].reshape(1,1)))
fig,axes = plt.subplots(1,1,figsize=(6,4))
VI=[np.var(model1)/np.mean(model1),np.var(model2)/np.mean(model2),np.var(model3)/np.mean(model3),np.var(model4)//np.mean(model4)]
Err=[np.mean(model1)-y0,np.mean(model2)-y0,np.mean(model3)-y0,np.mean(model4)-y0]
Err=pow(np.array(Err),2)
axes.plot(np.arange(1,5),preprocessing.scale(VI),marker='o',linestyle='-',label='方差')
axes.plot(np.arange(1,5),preprocessing.scale(Err),marker='o',linestyle='--',label='偏差')
axes.plot(np.arange(1,5),preprocessing.scale(MSEMean),marker='o',linestyle='-.',label="Err")
axes.set_ylabel('标准化值')
axes.set_xlabel('复杂度')
axes.set_title('不同复杂度模型的Err以及偏差和方差的变化趋势图')
axes.grid(linestyle="--", alpha=0.3)
plt.legend(loc='center',bbox_to_anchor=(0.5,0.8))
fig.show()
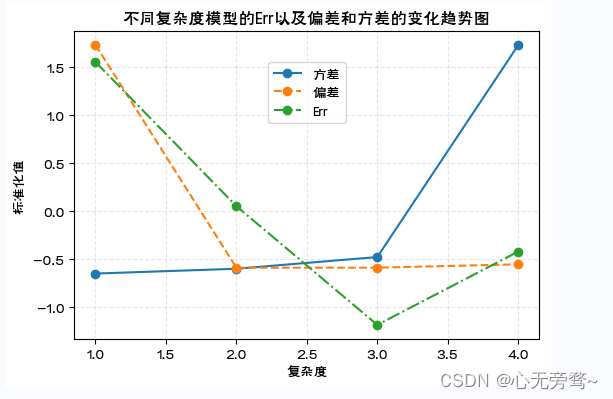
三、综合应用:空气污染的分类预测
- 建立空气污染预测的Logistic回归模型
data=pd.read_excel('北京市空气质量数据.xlsx')
data=data.replace(0,np.NaN)
data=data.dropna()
data['有无污染']=data['质量等级'].map({'优':0,'良':0,'轻度污染':1,'中度污染':1,'重度污染':1,'严重污染':1})
print(data['有无污染'].value_counts())
fig = plt.figure()
ax = fig.add_subplot(111)
flag=(data['有无污染']==0)
ax.scatter(data.loc[flag,'PM2.5'],data.loc[flag,'PM10'],c='cornflowerblue',marker='o',label='无污染',alpha=0.6)
flag=data['有无污染']==1
ax.scatter(data.loc[flag,'PM2.5'],data.loc[flag,'PM10'],c='grey',marker='+',label='有污染',alpha=0.4)
ax.set_xlabel('PM2.5')
ax.set_ylabel('PM10')
plt.legend()
##Logistic回归
X=data[['PM2.5','PM10']]
y=data['有无污染']
modelLR=LM.LogisticRegression()
modelLR.fit(X,y)
print("截距项:%f"%modelLR.intercept_)
print("回归系数:",modelLR.coef_)
print("优势比{0}".format(np.exp(modelLR.coef_)))
yhat=modelLR.predict(X)
print("预测结果:",yhat)
print("总的错判率:%f"%(1-modelLR.score(X,y)))
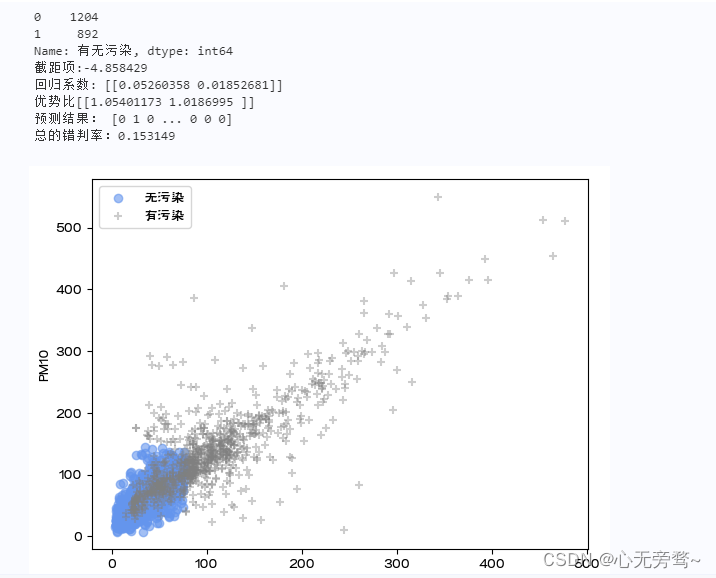
说明:
1、这里以空气质量监测数据为例,对是否有污染(二分类输出变量)进行预测。首先对数据进行预处理,将质量等级是优和良的合并为0类(无污染)共计1204天。其余合并为1类(有污染)共计892天。这里只考虑PM2.5和PM10对有无污染的影响,作为输入变量,只有0和1两个取值的有无污染作为输出变量。建立Logistic回归模型。
2、首先,modelLR=LM.LogisticRegression()定义modelLR对象为Logistic回归模型;然后,modelLR.fit(X,y)表示基于给出的X和y估计模型参数。其中,X为输入变量(矩阵形式),y为输出变量。
3、模型参数的估计值存储在intercept_和.coef_属性中,依次为截距项和回归系数。从回归系数估计值看,PM2.5(系数为0.05)对是否有污染的作用比PM10(系数为0.02)更大。
4、modelLR.predict(X)表示将X带入回归方程计算y的预测值。
- 优化模型及评价
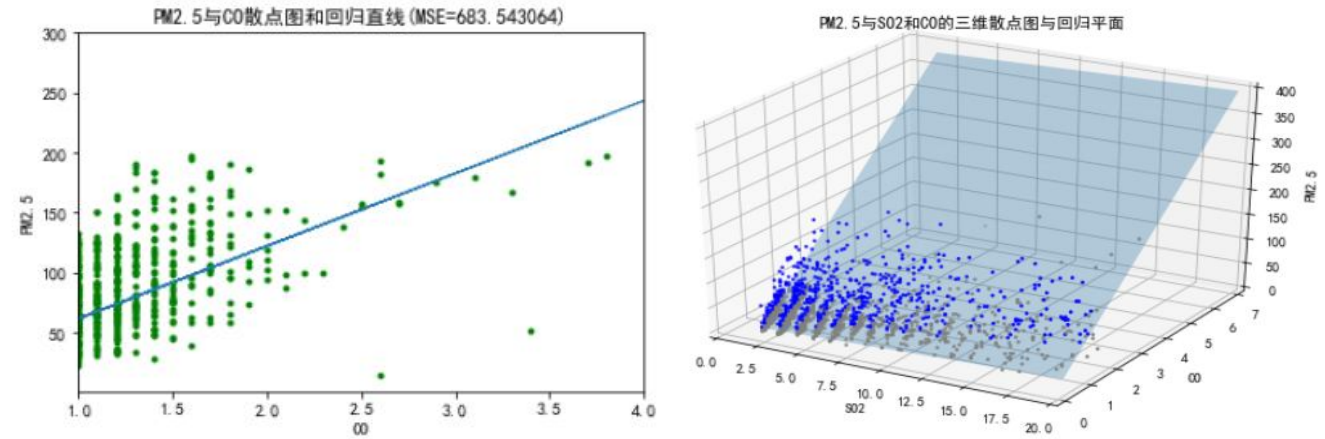
X=data.loc[:,['PM2.5','PM10','SO2','CO','NO2','O3']]
Y=data.loc[:,'有无污染']
modelLR=LM.LogisticRegression()
modelLR.fit(X,Y)
print('训练误差:',1-modelLR.score(X,Y)) #print(accuracy_score(Y,modelLR.predict(X)))
print('混淆矩阵:\n',confusion_matrix(Y,modelLR.predict(X)))
print('F1-score:',f1_score(Y,modelLR.predict(X),pos_label=1))
fpr,tpr,thresholds = roc_curve(Y,modelLR.predict_proba(X)[:,1],pos_label=1) ###计算fpr和tpr
roc_auc = auc(fpr,tpr) ###计算auc的值
print('AUC:',roc_auc)
print('总正确率',accuracy_score(Y,modelLR.predict(X)))
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,4))
axes[0].plot(fpr, tpr, color='r',linewidth=2, label='ROC curve (area = %0.5f)' % roc_auc)
axes[0].plot([0, 1], [0, 1], color='navy', linewidth=2, linestyle='--')
axes[0].set_xlim([-0.01, 1.01])
axes[0].set_ylim([-0.01, 1.01])
axes[0].set_xlabel('FPR')
axes[0].set_ylabel('TPR')
axes[0].set_title('ROC曲线')
axes[0].legend(loc="lower right")
pre, rec, thresholds = precision_recall_curve(Y,modelLR.predict_proba(X)[:,1],pos_label=1)
axes[1].plot(rec, pre, color='r',linewidth=2, label='总正确率 = %0.3f)' % accuracy_score(Y,modelLR.predict(X)))
axes[1].plot([0,1],[1,pre.min()],color='navy', linewidth=2, linestyle='--')
axes[1].set_xlim([-0.01, 1.01])
axes[1].set_ylim([pre.min()-0.01, 1.01])
axes[1].set_xlabel('查全率R')
axes[1].set_ylabel('查准率P')
axes[1].set_title('P-R曲线')
axes[1].legend(loc='lower left')
plt.show()
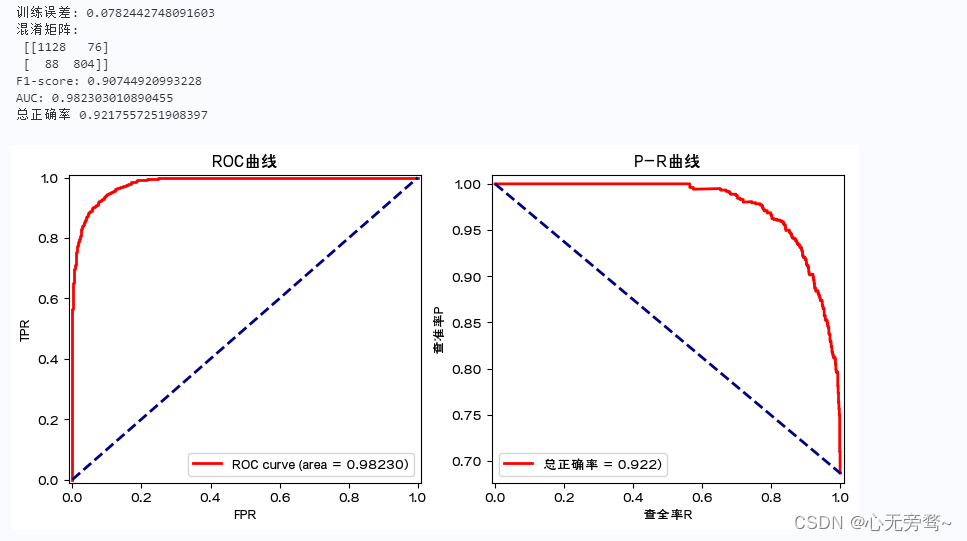
说明:
1、这里利用空气质量监测数据,建立Logistic回归模型对是否有污染进行分类预测。其中的输入变量包括PM2.5,PM10,SO2,CO,NO2,O3污染物浓度,是否有污染为二分类的输出变量(1为有污染,0为无污染)。进一步,对模型进行评价,涉及ROC曲线、AUC值以及F1分数等。需引用sklearn.metrics中的confusion_matrix,f1_score,roc_curve, auc,以及import accuracy_score等。
2、modelLR.score(X,Y)为预测模型的精度得分(基于训练集的)。分类预测的精度得分为总的预测正确率。也可通过accuracy_score函数得到同样结果。
3、confusion_matrix(Y,modelLR.predict(X)):计算模型的混淆矩阵。
4、f1_score(Y,modelLR.predict(X),pos_label=1):针对1类计算F1得分。
5、modelLR.predict_proba(X)中存储模型预测为0类和1类的概率,这里关心预测为1类的概率。
6、roc_curve:计算预测为1类的概率从大到小过程中的TPR和FPR。auc(fpr,tpr) 计算ROC曲线下的面积。
7、precision_recall_curve:计算预测为1类的概率从大到小过程中的查准率P和查全率R.
8、ROC曲线和AUC值,以及P-R曲线均表明,该预测模型的预测误差(训练误差)很小。
总结
在机器学习中,预测建模是十分关键的一步,特别是模型选择。模型选择在机器学习预测建模中具有非常重要的地位。模型选择的正确与否直接关系到预测的准确度和效果。在模型选择过程中,需要考虑多个因素,如模型的性能、泛化能力、计算成本、数据量等。
在选择模型时,需要考虑模型的性能指标,如准确率、精度、召回率、F1分数等。准确率是评估模型预测能力的重要指标,精度则可以衡量模型预测结果与实际结果之间的差异程度,召回率和F1分数则可以综合考虑模型的预测精度和召回能力。
此外,模型选择还需要考虑模型的计算成本和数据量的要求。对于大规模数据集,通常选择基于深度学习的模型,因为深度学习模型具有更好的计算能力和泛化能力。而对于小规模数据集,则可以选择基于机器学习的模型,因为这些模型可以更快地训练和解码数据。
最后,需要根据具体的应用场景和需求来选择合适的模型。不同的预测任务和数据特征需要选择不同的模型,例如在预测股票价格时,需要选择基于技术分析的模型,而在预测电影票房时,需要选择基于内容分析的模型。
因此,在机器学习预测建模中,模型选择是一个非常重要的环节,需要综合考虑多个因素,并根据实际情况进行选择。