文章目录
- 一，回归
- 1.1回归分析的基本概念
- 1.2线性回归
- 1.3最小二乘法
- 1.4一元(简单)线性回归模型
- 1.4.1随机误差项(线性回归模型)的假定条件
- 1.4.2参数的普通最小二乘估计(0LS)
- 1.5葡萄酒数据集的最小二乘法线性回归实例
一，回归
1.1回归分析的基本概念
回归分析（regression analysis)指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
- 确定变量之间是否存在相关关系，若存在，则找出数学表达式
- 根据一个或几个变量的值，预测或控制另一个或几个变量的值，且估计这种控制或预测可以达到何种精确度。
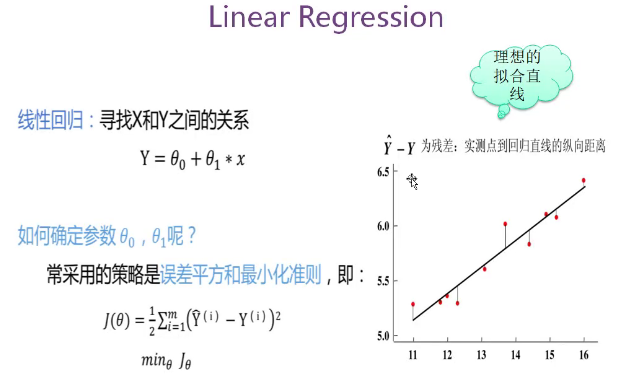
1.2线性回归
线性回归：线性模型就是对输入特征加权求和，再加上一个我们称为偏置项（也称为截距项)的常数，以此进行预测。
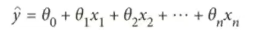
1.3最小二乘法
最小二乘法是一种在误差估计、不确定度、系统辨识及预测、预报等数据处理诸多学科领域得到广泛应用的数学工具。
最小二乘法是解决曲线拟合问题最常用的方法。其基本思路是：令
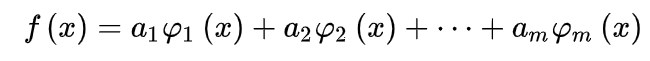
现在问题就转化为求J。的最小值问题。
具体的做法是:
1)对目标函数求导
2)零其导数为0,求得极值如果函数是凸函数,极值点就是最值点。这即是著名方法一最小二乘的基本思想。
1.4一元(简单)线性回归模型
建立两个变量之间的数学模型:
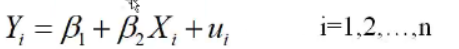
Y表示销售价格，称作被解释变量，X表示房屋面积，称作解释变量，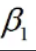
与
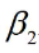为回归系数(待估参数)，u为随机误差项（也称随机扰动项)。
上式只含一个解释变量,变量间的关系是线性的,称为一元线性回归模型(简单线性回归模型)
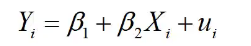
简单线性回归模型引入随机误差项，主要有以下几方面的原因：
1)作为未知影响因素的代表；
2)作为无法取得数据的己知因素的代表；
3)作为众多细小影响因素的综合代表；
4)模型的设定误差；
5)变量的观测误差；
6)经济现象的内在随机性。
1.4.1随机误差项(线性回归模型)的假定条件
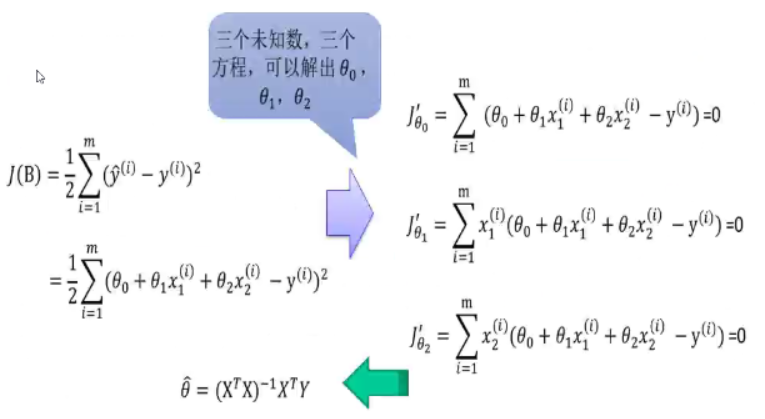
1.4.2参数的普通最小二乘估计(0LS)
为求总体参数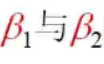
的估计值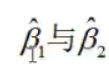
,使用普通最小二乘法。
普通最小二乘法(Ordinary least squares,.OLS)给出的判断标准是：拟合直线的残差平方和达到最小。
称为OLS估计量的离差形式(deviation form)。
由于参数的估计结果是通过最小二乘法得到的,故称为普通最小二乘估计量(ordinary leastsquares estimators)。
1.5葡萄酒数据集的最小二乘法线性回归实例
1.导入葡萄酒数据集
from sklearn.datasets import load_wine
wine = load_wine()
X = wine.data
y = wine.target
2.使用最小二乘法线性回归：
from sklearn import linear_model
linear = linear_model.LinearRegression()
3.对其进行预测：
import numpy as np
linear.fit(X[:,:1],y)
y_predicted = np.dot(X[:,:1],linear.coef_)+linear.intercept_
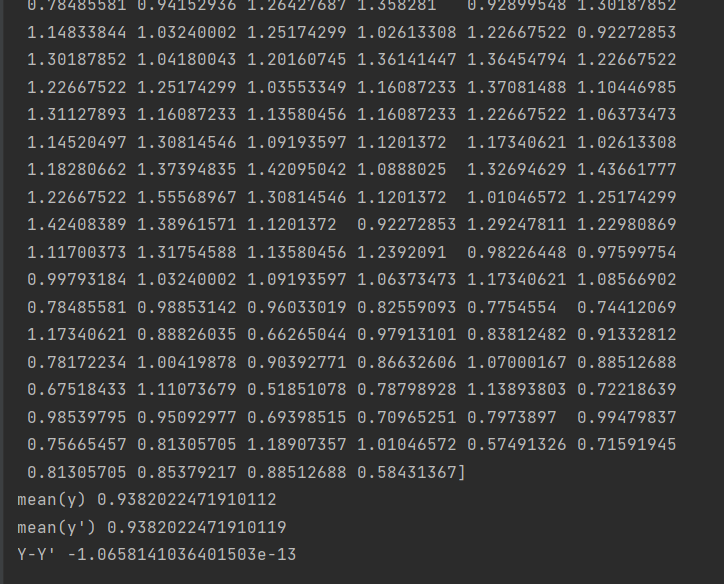
4.将预测值和，原本的值进行输出，和原本值减去预测值得到结果如下：
print("y",y_predicted)
print("mean(y)",np.mean(y))
print("mean(y')",np.mean(y_predicted))
print("Y-Y'",np.sum(y-y_predicted))
输出如下：
- 对13个特征进行俩俩组合，并且不重复：
linear = linear_model.LinearRegression()
x_list = []
for j in range(0, 13):
for i in range(j+1, 13):
6.输出13个特征进行俩俩组合的预测得分最大值：
if j != i:
print(j, i)
x_local = X[:, [j, i]]
linear.fit(x_local, y)
print("score", linear.score(x_local, y))
x_list.append(linear.score(x_local, y))
print(linear.coef_)
print(linear.intercept_)
print(x_list)
print("最大值为", max(x_list))
结果如下：
- 切分数据集：测试集 30%：
wine_X_train, wine_X_test, wine_y_train, wine_y_test = train_test_split(X, y, test_size=0.1*i, random_state=0)
8.线性回归进行训练得分：
from sklearn import linear_model
model = linear_model.LinearRegression()
model.fit(wine_X_train,wine_y_train)
train_score.append(model.score(wine_X_train,wine_y_train)*100)
test_score.append(model.score(wine_X_test,wine_y_test)*100)
print("train:",model.score(wine_X_train,wine_y_train))
print("test:",model.score(wine_X_test,wine_y_test))
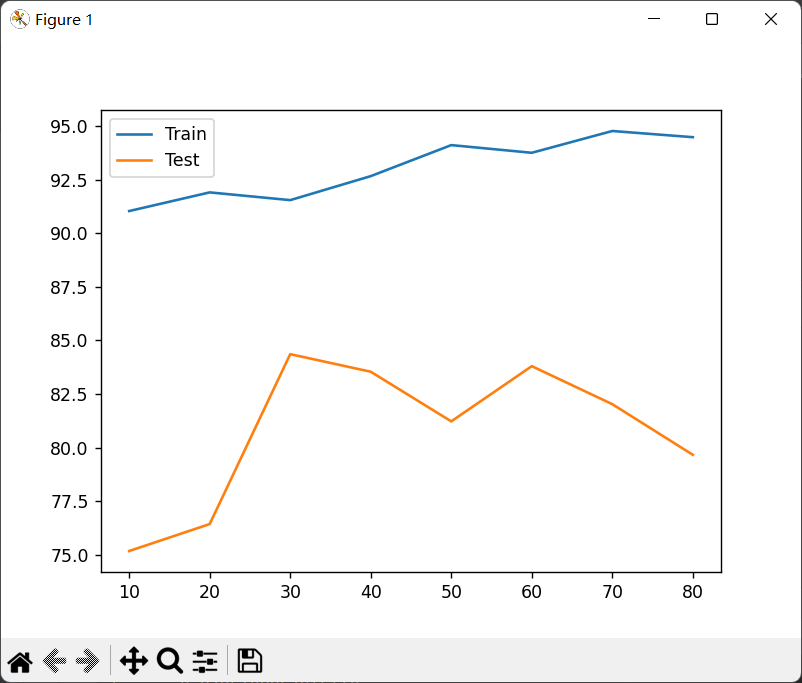
9.画图，可视化观察
plt.plot(x,train_score,label="Train")
plt.plot(x,test_score,label="Test")
plt.legend(loc='best')
plt.show()
输出如下：
train_score: [91.03676416293968, 91.9071553176753, 91.54585590997156, 92.66522947292925, 94.11247607913444, 93.75429953765662, 94.77044261319818, 94.48210580122965]
test_score: [75.18096058648021, 76.43759153956302, 84.36193575843113, 83.54234051618413, 81.22672208926059, 83.80201986070868, 82.0291448284772, 79.66827225108624]
结果如下：
