目录
分治策略
1.分治法可以解决的问题特征
2.分治法解题步骤
3.分治法编程举例
递归求阶乘
求斐波那契数列
小练习:给出一个数n,打印其每一位
分治策略
1.分治法可以解决的问题特征
(1)问题规模缩小到一定程度就可以轻易解决
(2)问题可以分解为若干个规模较小的相同类型问题
(3)使用小规模的解可以合并成该问题原规模的解
(4)该问题分解出的各个子问题相互独立
2.分治法解题步骤
(1)分解:将原问题划分为与原问题形式相同的子问题,只是规模减小。
(2)解决:递归求解子问题,如果子问题规模足够小则停止递归,直接求解。
(3)合并:将小规模的解合并为原规模问题的解。
3.分治法编程举例
递归求阶乘

(1)思想:不断缩小问题规模(要求n的阶乘,先求n-1的阶乘;要求n-1的阶乘,先求n-2的阶乘......)直至规模为1~求1的阶乘,再逐层返回合并解。
递归定义式如图: 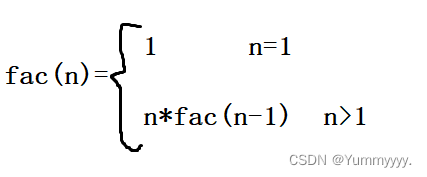
(2)代码实现(循环实现):
int fac(int n)
{
if (n <= 1) return 1;
int sum = 1;
for (int i = 2; i <= n; ++i)
{
sum *= i;
}
return sum;
}
int main()
{
int n = 0;
cin >> n;
cout << fac(n) << endl;
return 0;
}时间复杂度:O(n) 空间复杂度:S(1)
(3)代码实现(递归实现):
int fac(int n)
{
if (n <= 1) return 1;
return n * fac(n - 1);
}
int main()
{
int n = 0;
cin >> n;
cout << fac(n) << endl;
return 0;
}时间复杂度:O(n) 空间复杂度:S(n)
由于递归会开辟栈帧,故有额外空间开辟:空间复杂度S(n)
(4)补充:没有无限递归!!栈的空间是有限的,栈满会溢出。
求斐波那契数列
(1)思想:斐波那契数列(1 1 2 3 5 8 12 21.....),递归求解。当n>2时,fib(n)=fib(n-1)+fib(n-2);
递归定义式如图: 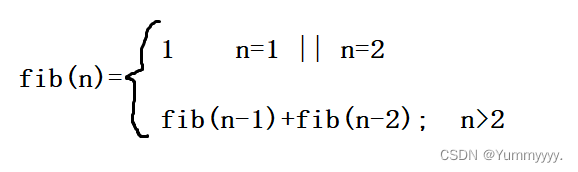
(2)代码实现(循环实现):

int fib(int n)
{
int a = 1, b = 1, c = 1;//c初值为1,避免写n==1||n=2时return 1
//if(n==1||n==2) return 1;
for (int i = 3; i <= n; ++i)
{
c = a + b;
a = b;
b = c;
}
return c;
}
int main()
{
int n = 0;
cin >> n;
cout << fib(n) << endl;
return 0;
}(3)代码实现(递归实现):
int fib(int n)
{
if (n == 1 || n == 2) return 1;
return fib(n - 1) + fib(n - 2);
}
int main()
{
int n = 0;
cin >> n;
cout << fib(n) << endl;
return 0;
}时间复杂度:O(n) 空间复杂度:S(n)
小练习:给出一个数n,打印其每一位
(1)代码实现(循环实现):
void PrintInt(int n)
{
if (n < 0) return;
while (n != 0)
{
printf("%d ", n % 10);
n /= 10;
}
}
int main()
{
int n = 0;
cin >> n;
PrintInt(n);
return 0;
}(2)代码实现(递归实现):
void PrintInt(int n)
{
if (n <= 0) return;
printf("%d ", n % 10);
PrintInt(n / 10);
}
int main()
{
int n = 0;
cin >> n;
PrintInt(n);
return 0;
}