💥💥💥💞💞💞欢迎来到本博客❤️❤️❤️💥💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现+数据+文章讲解
💥1 概述
在过去二十年中,光学频率梳的发明使得能够在电磁光谱1-3的大部分范围内对多个原子和分子跃迁的能量值进行高度精确的测量。精确的绝对频率校准在基础物理中起着关键作用的领域之一是分子氢及其同位素的光谱研究,其跃迁频率可以通过理论精确预测4。理论与实验之间的比较代表了分子量子电动力学5(QED)的试验台,也是探索标准模型6–8之外的物理或确定基本量(如核子-电子质量比)的有力方法9。
频率梳彻底改变了光学频率计量,允许 确定大量分子的高精度跃迁频率 物种。尽管人们公认了科学兴趣,但这些进展只有 边际受益的红外非活动跃迁,因为它们固有的 弱截面。在这里,我们通过引入 受激拉曼散射计量,其中利用频率梳 校准泵浦和斯托克斯激发激光器之间的频率失谐。 我们将这种方法应用于分子氢来测试量子电动力学。 我们测量 H 的 Q(1) 基本线的跃迁频率2约 4155 厘米−1不确定性只有十亿分之一,即 与从头算的理论基准相当,超过 比实验技术状态好十年。我们的梳状校准 受激拉曼散射光谱仪扩展了光学工具箱 频率计量,因为它可以通过简单的技术更改应用于 许多其他红外非活动跃迁,超过50-5000厘米。−1范围 也覆盖。
📚2 运行结果





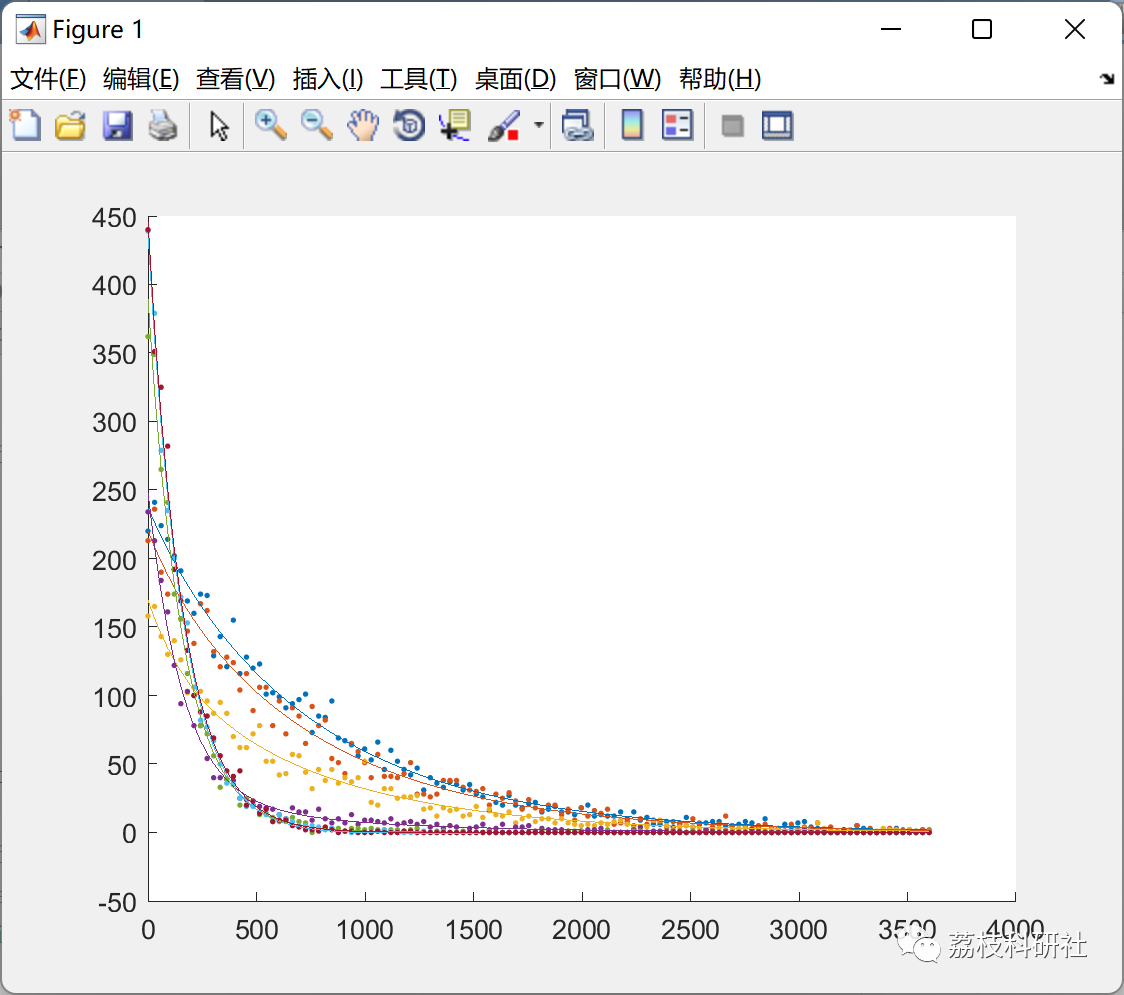



部分代码:
% Example for the global fit class (GlobalFitSimple)
% Consider multiple datasets with a linear dependence on the independent
% variable, all with the same slope but different vertical positions.
% Perform a global fit of the parameters of the linear function.
clear all
close all
rng(1) % Set a seed for the random number generation (for reproducibility)
model = @(x, p) p(1)*x + p(2); % Linear function
% Parameters for the simulated datasets
% Four datasets (one row per dataset): shifted lines
pars = [0.3, -0.2;
0.3, 2;
0.3, 3.4;
0.3, 1.7];
N = 20; % Points per line
noise = 0.05; % Absolute noise level
% Generate and plot data
figure()
hold on
for i=1:size(pars, 1)
xData{i} = linspace(-2, 5, N);
yData{i} = model(xData{i}, pars(i,:)) + noise*randn(size(xData{i}));
plot(xData{i}, yData{i}, '.')
end
hold off
gf = GlobalFitSimple(); % Instantiate the class
gf.setData(xData, yData); % Set the data to fit
% 2 -> number of parameters. The last array tells whether a parameter is local or global
gf.setModel(model, 2, [1 0])
gf.setStart(pars) % Set start point (for all data)
gf.fit() % Run the fit!
fit_pars = gf.getFittedParameters() % Retrieve the fitted parameters...
fit_errs = gf.getParamersErrors() % ...and their errors
% Evaluate and plot the fit
hold on
for i=1:size(pars, 1)
yData{i} = model(xData{i}, fit_pars(i,:));
plot(xData{i}, yData{i}, '-')
end
hold off
🎉3 参考文献