💥💥💥💞💞💞欢迎来到本博客❤️❤️❤️💥💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
目录
💥1 概述
1.1 Copula函数定义
1.2 Copula函数类型
📚2 运行结果
2.1 方案1
2.2 方案2
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
1.1 Copula函数定义
Copula最早由Sklar在1959年提出,即Sklar定理。
以二维变量为例,F(x)与G(y)分别为变量X与Y的边缘分布函数,由式(1)可知,若H(x,y)为F(x)与G(y)的联合分布函数,那么存在唯一的Copula函数C,可以将联合分布函数与边缘分布函数进行连接。
Sklar定理认为[19]一个联合分布函数的相关性性质完全由其Copula函数所确定。换言之,变量的随机性可用其各自的边缘分布进行描述,而变量之间的耦合特性需由Copula函数进行表示。N个随机变量的联合分布可分解为N个变量各自的边缘分布以及一个Copula函数,将变量的随机性和耦合性分离,达到减少联合分布函数求解难度的目的。
1.2 Copula函数类型
常用的Copula函数分为椭圆族Copula函数与阿基米德Copula函数两类。椭圆族Copula函数包括正态Copula函数与t-Copula函数,两者均有对称的尾部相关性,在中心区域差别不大。阿基米德Copula函数具有统一的分布函数表达式:
式中: u1,u2,…,UN——随机变量边缘分布; ——阿基米德Copula函数生成元。
根据不同的生成元函数能得到不同的阿基米德Copula函数,常见的有Frank Copula(Fr-Copula)函数、Clayton Copula(Clay-Copula)函数以及Gumbel Copula(Gum-Copula)函数,3种阿基米德Copula函数生成元如表1所示。

不同类型的Copula函数具有不同的特性,因而对于相关性的描述也有所不同。其中椭圆族Copula函数与Fr-Copula函数侧重于刻画对称的尾部相关性,而Clay-Copula函数与Gum-Copula函数则更适合描述非对称的上尾特性和非对称的下尾特性。如果只应用某种单一Copula函数进行数据拟合分析相关性,容易出现失真状况,导致相关性分析不准确。因此可选择将几种Copula函数组合,构造混合Copula函数模型进行数据相关性的分析。
📚2 运行结果
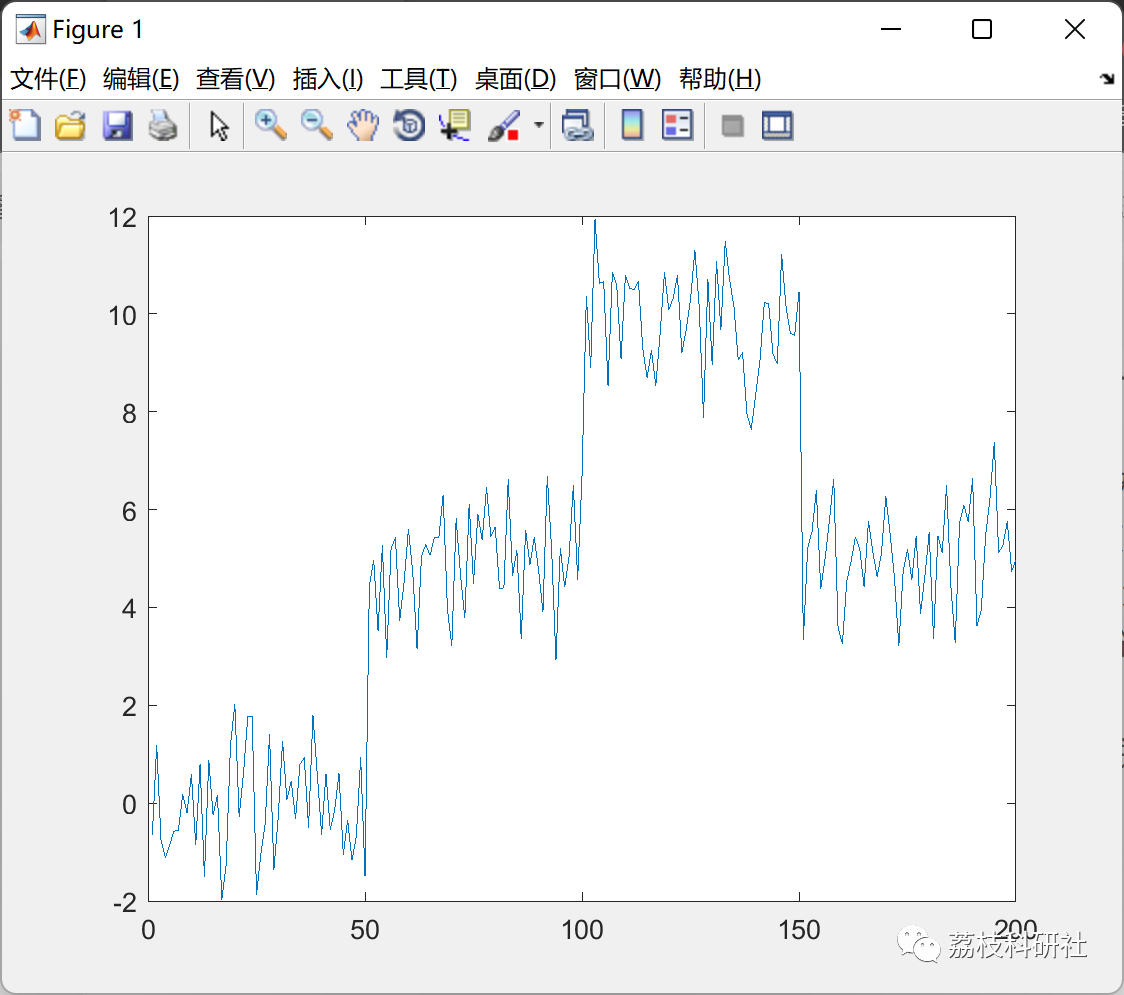
2.1 方案1
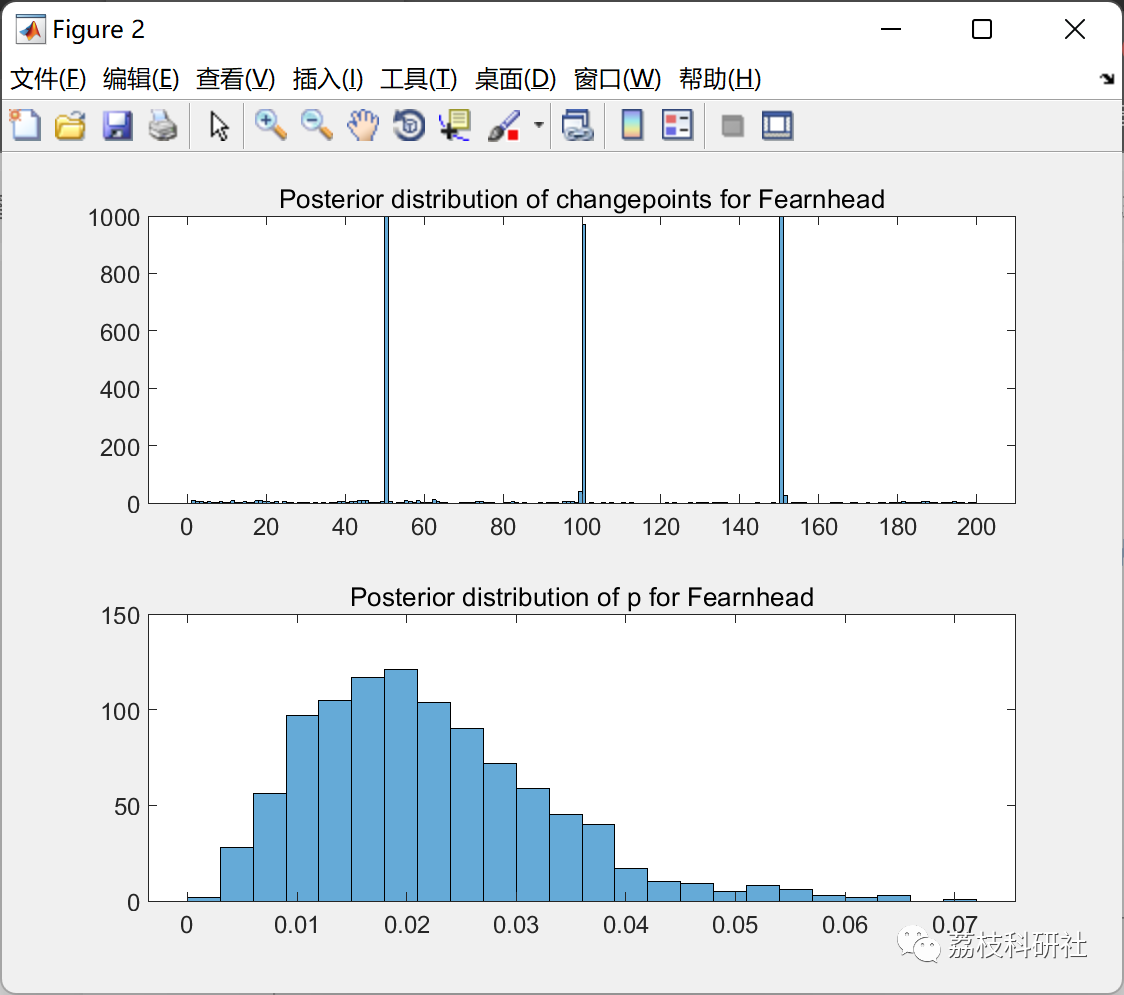
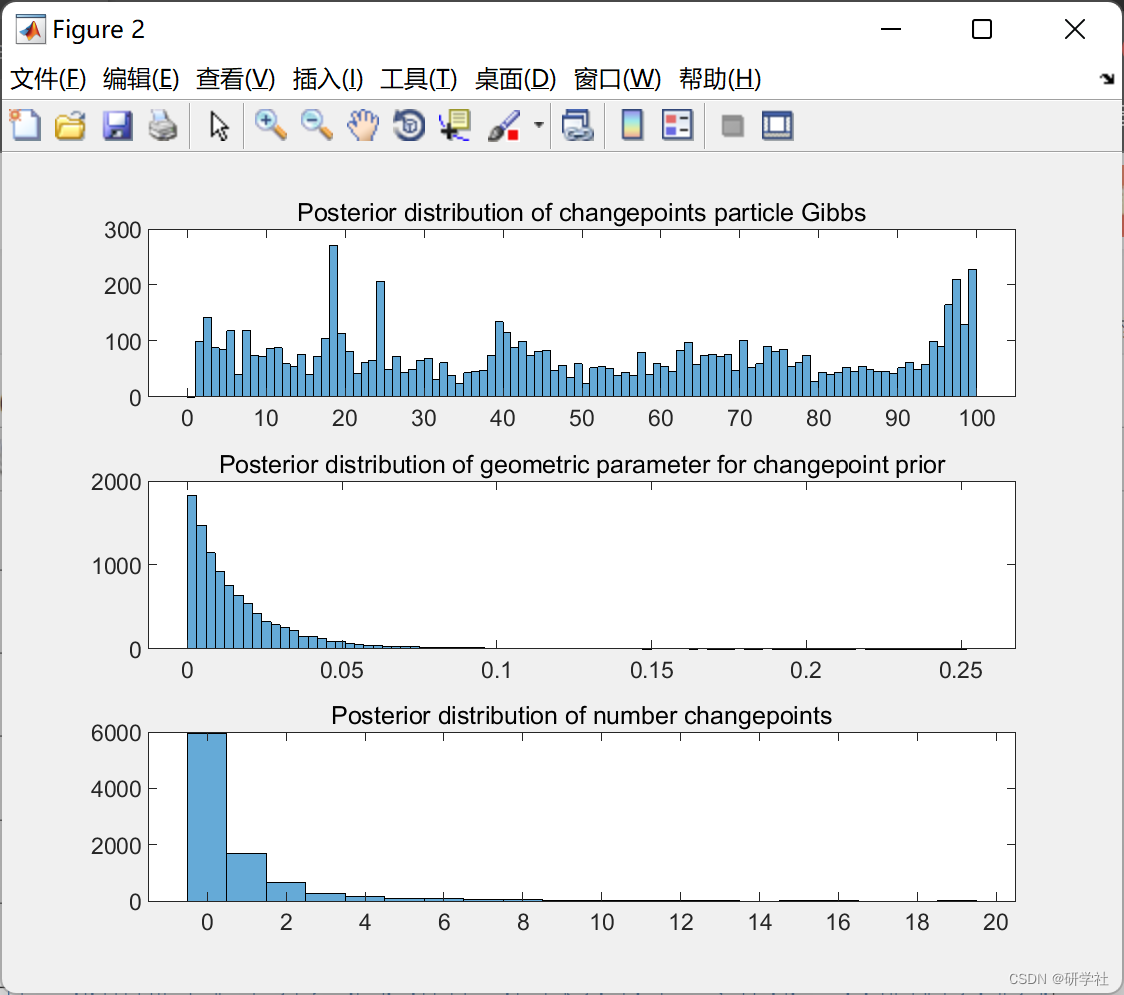
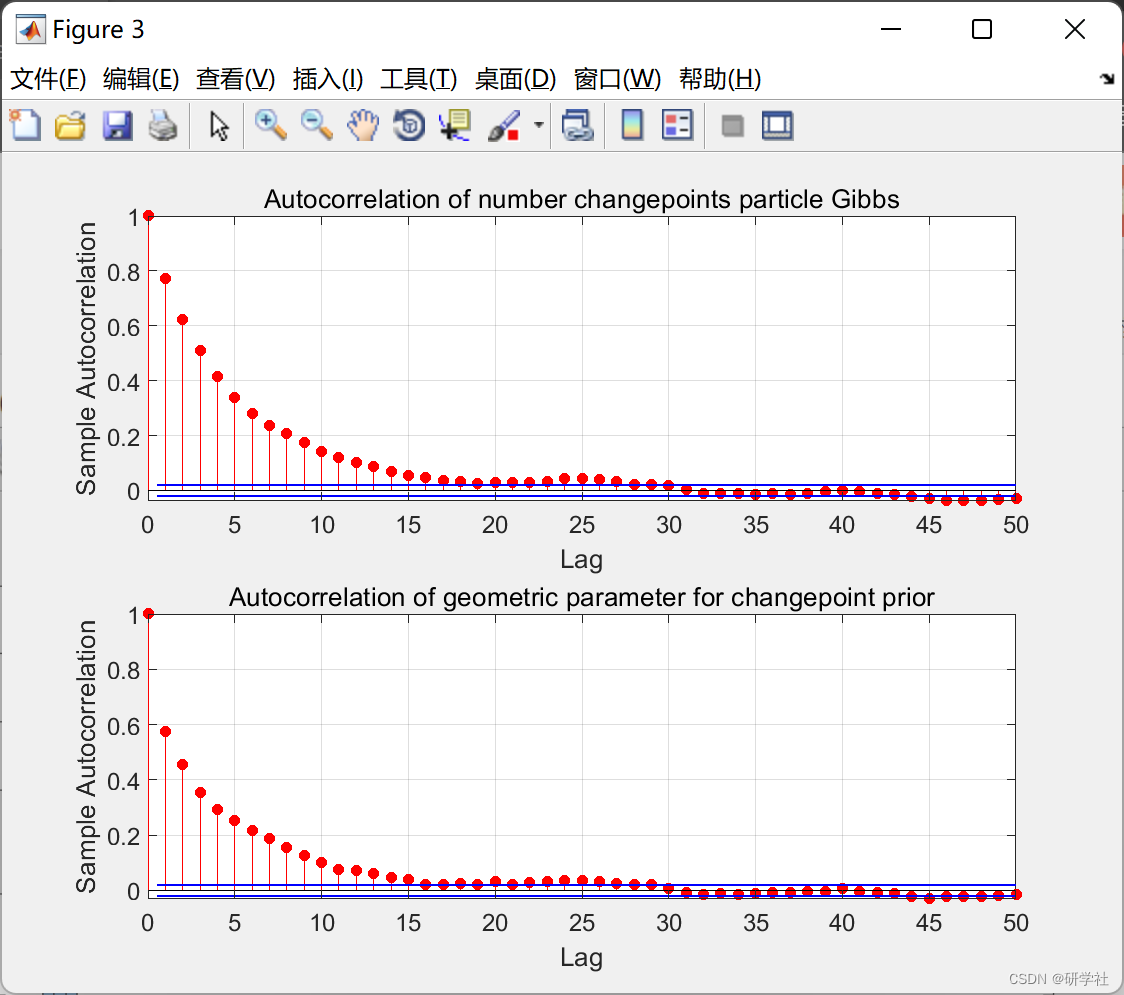
2.2 方案2
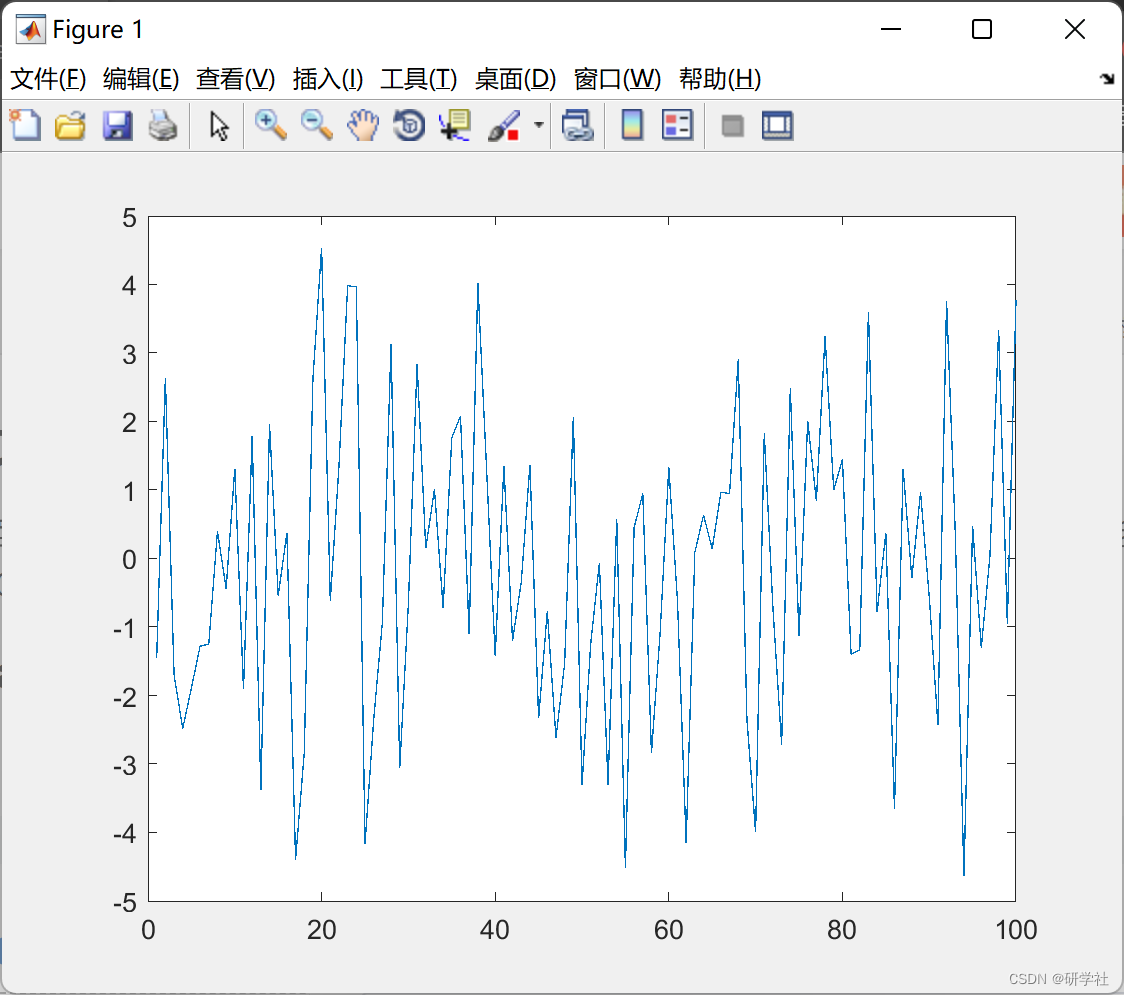
🎉3 参考文献
[1]黄宇,张冰哲,庞慧珍,徐璟,刘磊,王彪.基于混合Copula优化算法的风速预测方法研究[J].太阳能学报,2022,43(10):192-201.DOI:10.19912/j.0254-0096.tynxb.2021-0431.