版权声明：原创不易，本文禁止抄袭、转载，侵权必究！

一、Karatsuba 乘法

当你在纸上做两个数字的乘法时，一般我们都是用小时候学到的方法：



这个计算方式的时间复杂度是 O(n²)，但有没有其他的方法加速相乘的计算速度呢？

Karatsuba 乘法是一种快速乘法。此算法在1960年由 Anatolii Alexeevitch Karatsuba 提出，并于1962年得以发表。此算法主要用于两个大数相乘。普通乘法的时间复杂度是O(n²)，而 Karatsuba 算法的复杂度仅为O(3nlog2(3))

二、算法思路

可以注意到 AD +BC 这个计算需要两个 O(n²/4) 的乘法和一个 O(n) 的加法。

(A+B)(C+D)-AC-BD = AC+AD+BC+BD-AC-BD = AD + BC

Karatsuba 把这个原始的计算改成上面这个计算，因为 AC 和 BD 是已知的，因此现在的 AD +BC 的时间复杂度变成了 一个 O(n²/4) 的乘法和四个 O(n) 的加法或减法，达到 O(n^log2(3)) 的时间复杂度

三、Python算法实现

import numpy as np
from itertools import zip_longest

def add(x, y):
  z, carry = [], 0
  for r, s in zip_longest(x, y, fillvalue=0):   #以元素多的为基准，少的填充0
    t = r + s + carry
    carry = t // 10   #除法取整
    z.append(t % 10)  #取余
  if carry:
    z.append(carry)
  return z

def sub(x, y):
  z, carry = [], 0
  for r, s in zip_longest(x, y, fillvalue=0):
    t = r - s + carry
    carry = t // 10
    z.append(t % 10)
  return z

def karatsuba(x, y):
  # 确保长度相同
  while len(x) < len(y):
    x.append(0)
  while len(x) > len(y):
    y.append(0)

  # 长度和分割
  n = len(x)
  n_2 = (n + 1) >> 1

  # 长度等于1的情况
  if n == 1:
    return add([x[0] * y[0]], [])

  # 分割后进行赋值
  x0, x1 = x[:n_2], x[n_2:]
  y0, y1 = y[:n_2], y[n_2:]

  # karatsuba algorithm
  z0 = karatsuba(x0, y0)
  z1 = karatsuba(x1, y1)
  z2 = karatsuba(add(x0, x1), add(y0, y1))
  z2 = sub(sub(z2, z0), z1)

  z = add(z0, [0] * (n_2 << 1) + z1)
  z = add(z, [0] * n_2 + z2)

  return z

x, y = '53568757', '82567936'
def mult(x, y):
  print(x, '*', y, '=', int(x) * int(y))

  x = list(map(int, reversed(x)))
  y = list(map(int, reversed(y)))
  z = karatsuba(x, y)

  print(''.join(map(str, reversed(z))))

mult(x,y)

输出结果：

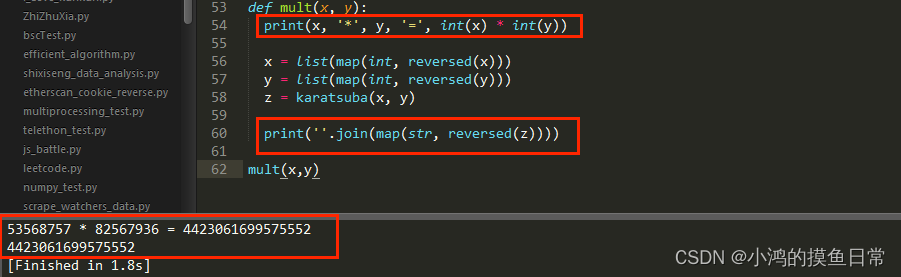
如图所示，输出结果正确

四、作者Info

Author：小鸿的摸鱼日常，Goal：让编程更有趣！

专注于算法、爬虫，游戏开发，数据分析、自然语言处理，AI等，期待你的关注，让我们一起成长、一起Coding！

版权说明：本文禁止抄袭、转载 ，侵权必究！