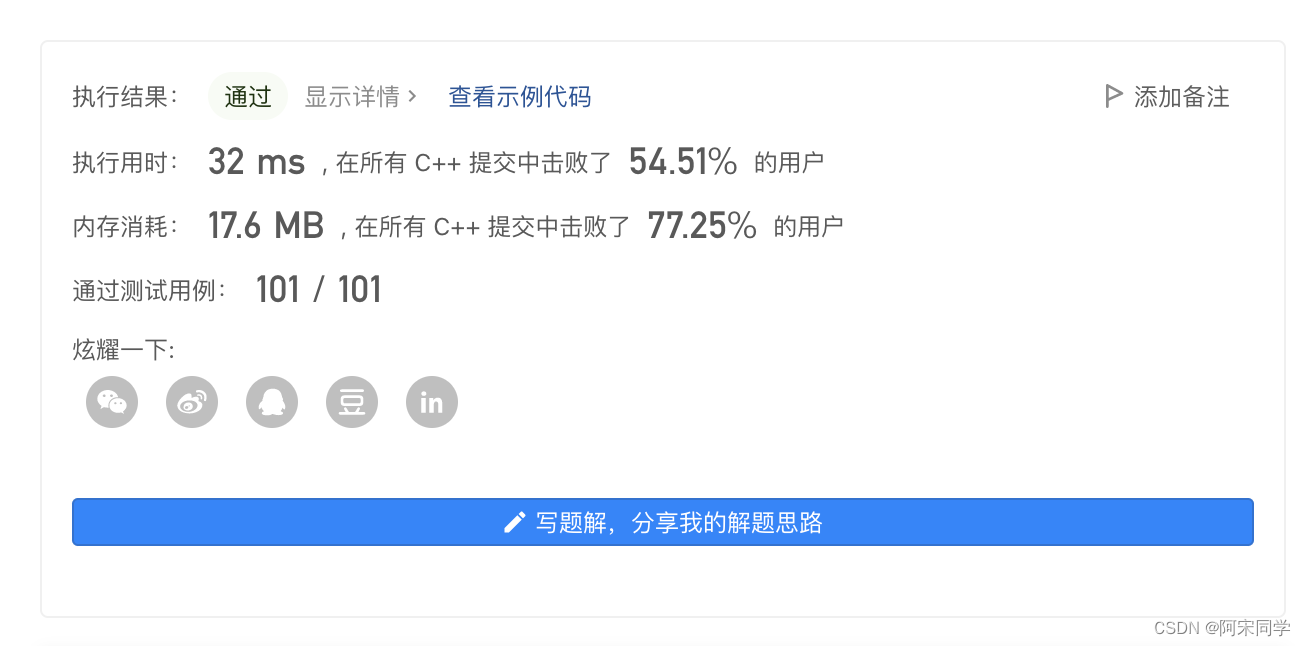
文章目录
- 一、Zero Forcing 算法思想
- 二、MMSE
- 三、MIMO检测中 Zero Forcing 算法比 Maximum Likelihood 差的思考
本篇文章是学习了B站UP主 乐吧的数学 之后的笔记总结,老师讲的非常好,大家有兴趣的可以关注一波!
一、Zero Forcing 算法思想
那么 Maximum Likelihood(ML) 算法是最优的检测,这个最优指的是使错误率最低(假定发送的 x 是等概率出现的),从最低错误率的角度出发,同时假定在每个天线处的高斯白噪声是独立同分布的,那么,这个 ML 算法的公式为:
X
^
=
argmin
X
∈
X
M
t
∥
Y
−
H
X
∥
2
(1)
\hat{X}=\operatorname{argmin}_{X \in \mathcal{X}^{M_{t}}}\|Y-H X\|^{2}\tag1
X^=argminX∈XMt∥Y−HX∥2(1)
遍历 X X X 的所有可能取值,找到是公式 (1) 最小的。
因为公式 (1) 的计算量非常大,在实际中是不可行的。那么对公式 (1) 放开条件,让 X 的取值,不仅限于星座图中的值,而是任何值,那么,这个就是 zero forcing(ZF) 算法的出发点,则公式 (1) 就变成
X
^
=
argmin
X
∥
Y
−
H
X
∥
2
(2)
\hat{X}=\operatorname{argmin}_{X}\|Y-H X\|^{2}\tag2
X^=argminX∥Y−HX∥2(2)
注意 argmin 的下表中的 X ,没有做任何限制。公式 (2) 就是一个无约束的最优化问题,我们令:
f
(
X
)
=
∥
Y
−
H
X
∥
2
(3)
f(X)=\|Y-H X\|^{2}\tag3
f(X)=∥Y−HX∥2(3)
接下来对公式 (3) 做进一步的推导(我们约定所有的向量都是列向量):
f ( X ) = ∥ Y − H X ∥ 2 = ( Y − H X ) H ( Y − H X ) = ( Y H − X H H H ) ( Y − H X ) = Y H Y − Y H H X − X H H H Y + X H H H H X (4) \begin{aligned} f(X) & =\|Y-H X\|^{2} \\ & =(Y-H X)^{H}(Y-H X) \\ & =\left(Y^{H}-X^{H} H^{H}\right)(Y-H X) \\ & =Y^{H} Y-Y^{H} H X-X^{H} H^{H} Y+X^{H} H^{H} H X \end{aligned}\tag4 f(X)=∥Y−HX∥2=(Y−HX)H(Y−HX)=(YH−XHHH)(Y−HX)=YHY−YHHX−XHHHY+XHHHHX(4)
把公式 (4) 对 X X X 求导,公式 (4) 实际上是一个数, X X X 是一个向量,这个求导的过程,实际上就是对 (4) 用 X X X 的每个分量分别求一次导数并令其等于 0,得到 N N N ( 假如 X X X 是 N N N 维的列向量) 个方程,联合起来可以求解出 X 的每个分量。用矩阵形式来写就是
∂ Y H H X ∂ X = H H Y \frac{\partial Y^{H} H X}{\partial X}=H^{H} Y ∂X∂YHHX=HHY
∂ X H H H Y ∂ X = H H Y \frac{\partial X^{H} H^{H} Y}{\partial X}=H^{H} Y ∂X∂XHHHY=HHY
∂ X H H H H X ∂ X = 2 H H H X \frac{\partial X^{H} H^{H} H X}{\partial X}=2 H^{H} H X ∂X∂XHHHHX=2HHHX
则
0
−
H
H
Y
−
H
H
Y
+
2
H
H
H
X
=
0
0-H^{H} Y-H^{H} Y+2 H^{H} H X=0
0−HHY−HHY+2HHHX=0
进一步推导
H H H X = H H Y H^{H} H X=H^{H} Y HHHX=HHY
最后:
X
~
=
(
H
H
H
)
−
1
H
H
Y
(5)
\tilde{X}=\left(H^{H} H\right)^{-1} H^{H} Y\tag5
X~=(HHH)−1HHY(5)
如果 H H H 是方阵且可逆,公式 (5) 可以写成:
X ~ = H − 1 ( H H ) − 1 H H Y = H − 1 Y \begin{aligned} \tilde{X} & =H^{-1}\left(H^{H}\right)^{-1} H^{H} Y \\ & =H^{-1} Y \end{aligned} X~=H−1(HH)−1HHY=H−1Y
这样得出的值,就是检测后的估计值,即用 Zero Forcing 算法估计出来的值。下面我们这个值用 X ~ \tilde{X} X~ 来表示。
将 Y = H X + W Y=H X+W Y=HX+W 代入
X ~ = ( H H H ) − 1 H H ( H X + W ) = X + ( H H H ) − 1 H H W = X + H − 1 W = X + W ~ \begin{aligned}\tilde{X}&=\left(H^{H} H\right)^{-1} H^{H}(H X+W)\\ &=X+\left(H^{H} H\right)^{-1} H^{H} W\\ &=X+H^{-1}W\\ &=X+\tilde{W} \end{aligned} X~=(HHH)−1HH(HX+W)=X+(HHH)−1HHW=X+H−1W=X+W~
然后,再做解调检测
X ^ = argmin X ∈ X M t ∥ X ~ − X ∥ 2 (7) \begin{aligned} \hat{X}=\operatorname{argmin}_{X \in \mathcal{X}^{M_{t}}}\|\tilde{X}-X\|^{2} \end{aligned}\tag7 X^=argminX∈XMt∥X~−X∥2(7)
X ∈ X M t X \in \mathcal{X}^{M_{t}} X∈XMt 是因为输出信号是从 M t M_t Mt 个天线中传输出来的信号。
我们将最大似然估计的算法拿下来比较一下
X ^ = argmin X ∈ X M t ∥ Y − H X ∥ 2 \hat{X}=\operatorname{argmin}_{X \in \mathcal{X}^{M_{t}}}\|Y-H X\|^{2} X^=argminX∈XMt∥Y−HX∥2
会发现其实这是两种思想方法,一个是在发送信号端进行比较,一个是在接收端进行比较。同时误差的来源都是接收端附加的噪声 W W W。但是Zero Forcing的优越处在于 X ~ \tilde{X} X~ 的值只要计算一次,就可以与 X ∈ X M t X \in \mathcal{X}^{M_{t}} X∈XMt 中的值进行比较,计算量会减小。
二、MMSE
G = ( H H H + σ 2 I ) − 1 H H G=\left(H^{H} H+\sigma^{2} I\right)^{-1} H^{H} G=(HHH+σ2I)−1HH
即:
X ~ = G Y = G H X + G W = ( H H H + σ 2 I ) − 1 H H H X + ( H H H + σ 2 I ) − 1 H H W \tilde{X}=G Y=G H X+G W=\left(H^{H} H+\sigma^{2} I\right)^{-1} H^{H} H X+\left(H^{H} H+\sigma^{2} I\right)^{-1} H^{H} W X~=GY=GHX+GW=(HHH+σ2I)−1HHHX+(HHH+σ2I)−1HHW
噪声小的时候,应该类似于 Zero Forcing,当噪声比较大时,接近 Matched Filter。
这里有一个有趣的现象,当噪声比较小的时候,MMSE 还是比 ZF 要好。有人专门对这个现象进行了理论分析,感兴趣的可以去阅读文献:
Y. Jiang, M. K. Varanasi and J. Li, “Performance Analysis of ZF and MMSE Equalizers for MIMO Systems: An In-Depth Study of the High SNR Regime,” in IEEE Transactions on Information Theory, vol. 57, no. 4, pp. 2008-2026, April 2011, doi: 10.1109/TIT.2011.2112070.
三、MIMO检测中 Zero Forcing 算法比 Maximum Likelihood 差的思考
我们假设这里 H H H 是方阵并且是可逆的
X ~ = H − 1 Y \tilde{X}=H^{-1} Y X~=H−1Y
Zero Forcing 算法于是有:
X ^ = argmin X ∈ X M t ∥ X ~ − X ∥ 2 = argmin X ∈ X M t ∥ H − 1 Y − X ∥ 2 = argmin X ∈ X M t ∥ H − 1 ( Y − H X ) ∥ 2 \begin{aligned} \hat{X} & =\operatorname{argmin}_{X \in \mathcal{X}^{M_{t}}}\|\tilde{X}-X\|^{2} \\ & =\operatorname{argmin}_{X \in \mathcal{X}^{M_{t}}}\left\|H^{-1} Y-X\right\|^{2} \\ & =\operatorname{argmin}_{X \in \mathcal{X}^{M_{t}}}\left\|H^{-1}(Y-H X)\right\|^{2} \end{aligned} X^=argminX∈XMt∥X~−X∥2=argminX∈XMt H−1Y−X 2=argminX∈XMt H−1(Y−HX) 2
这里假定
H
H
H 是方阵且可逆的,则
H
H
H 的逆矩阵也可以做
S
V
D
SVD
SVD 分解:
H
−
1
=
U
Σ
V
H
H^{-1}=U \Sigma V^{H}
H−1=UΣVH
则公式变为
∥ H − 1 ( Y − H X ) ∥ 2 = ∥ U Σ V H ( Y − H X ) ∥ 2 \left\|H^{-1}(Y-H X)\right\|^{2}=\left\|U \Sigma V^{H}(Y-H X)\right\|^{2} H−1(Y−HX) 2= UΣVH(Y−HX) 2
我们把 看成一个向量,则矩阵 U U U 因为是单位正交矩阵,所以,是一个刚性旋转,不改变被作用的向量的长度,因此 公式可以继续推导为:
∥ H − 1 ( Y − H X ) ∥ 2 = ∥ Σ V H ( Y − H X ) ∥ 2 \left\|H^{-1}(Y-H X)\right\|^{2}=\left\|\Sigma V^{H}(Y-H X)\right\|^{2} H−1(Y−HX) 2= ΣVH(Y−HX) 2
公式 (8) 中,我们把
Y
−
H
X
Y- HX
Y−HX 看成一个向量,记为
Z
Z
Z,则
V
H
V^H
VH 是对这个向量
Z
Z
Z 做旋转,不改变向量长度,旋转后的向量记为
Z
^
\hat{Z}
Z^, 则矩阵
Σ
\Sigma
Σ,是对向量各个分量进行缩放:
Σ
=
[
λ
1
⋯
λ
N
]
\Sigma=\left[\begin{array}{lll} \lambda_{1} & & \\ & \cdots & \\ & & \lambda_{N} \end{array}\right]
Σ=
λ1⋯λN
情况一: 所有特征值都相等
当 λ 1 = ⋯ = λ N = λ \lambda_{1}=\cdots=\lambda_{N}=\lambda λ1=⋯=λN=λ 时,公式可以写成:
∥ H − 1 ( Y − H X ) ∥ 2 = ∥ Σ V H ( Y − H X ) ∥ 2 = ∥ λ I V H ( Y − H X ) ∥ 2 = λ 2 ∥ V H ( Y − H X ) ∥ 2 \left\|H^{-1}(Y-H X)\right\|^{2}=\left\|\Sigma V^{H}(Y-H X)\right\|^{2}=\left\|\lambda I V^{H}(Y-H X)\right\|^{2}=\lambda^{2}\left\|V^{H}(Y-H X)\right\|^{2} H−1(Y−HX) 2= ΣVH(Y−HX) 2= λIVH(Y−HX) 2=λ2 VH(Y−HX) 2
因为 V H V^H VH 是单位正交的矩阵,因此,是一个刚性旋转,不改变后面向量的长度,因此公式可以写成:
∥ H − 1 ( Y − H X ) ∥ 2 = λ 2 ∥ ( Y − H X ) ∥ 2 \left\|H^{-1}(Y-H X)\right\|^{2}=\lambda^{2}\|(Y-H X)\|^{2} H−1(Y−HX) 2=λ2∥(Y−HX)∥2
这种情况下, Zero Forcing 算法就与 Maximum Likelihood 算法的性能一致。
情况二:噪声非常小,趋近于 0
公式中,一定能找到一个 X X X 向量,使得 Y − H X Y - HX Y−HX 为 0 0 0 向量,因为是 0 0 0 向量,所以,这个就是最小值,不可能找到另外一个向量 X ′ X' X′ ,使得结果比 0 小。所以,在噪声为 0 0 0 的情况下,Zero Forcing 算法就与 Maximum Likelihood 算法的性能一致。
情况三:特征值不全都相等,也含有噪声
∥
H
−
1
(
Y
−
H
X
)
∥
2
=
∥
Σ
V
H
(
Y
−
H
X
)
∥
2
=
∥
[
λ
1
Z
^
1
⋯
λ
N
Z
^
N
]
∥
2
=
λ
1
2
∥
Z
^
1
∥
2
+
⋯
+
λ
1
N
∥
Z
^
N
∥
2
\begin{aligned} \left\|H^{-1}(Y-H X)\right\|^{2} & =\left\|\Sigma V^{H}(Y-H X)\right\|^{2} \\ & =\left\|\left[\begin{array}{c} \lambda_{1} \hat{Z}_{1} \\ \cdots \\ \lambda_{N} \hat{Z}_{N} \end{array}\right]\right\|^{2} \\ & =\lambda_{1}^{2}\left\|\hat{Z}_{1}\right\|^{2}+\cdots+\lambda_{1}^{N}\left\|\hat{Z}_{N}\right\|^{2} \end{aligned}
H−1(Y−HX)
2=
ΣVH(Y−HX)
2=
λ1Z^1⋯λNZ^N
2=λ12
Z^1
2+⋯+λ1N
Z^N
2
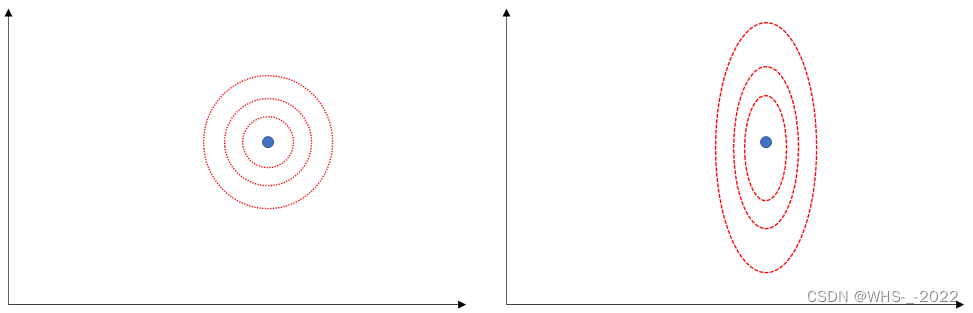
公式上面公式中第一个等号那里,相当于对向量 Y − H X Y-HX Y−HX 先做旋转,然后再在各个维度上做缩放,例如都是都是逆时针旋转一个固定角度,两个维度分别是放大三倍和缩小一倍(以二维向量为例子,方便画图理解),则不同的向量,即使长度相同,但是角度不同,经过旋转和缩放后,长度将会不同。
下图蓝色是初始向量,旋转后变成绿色向量,然后经过 X 轴放大3倍, Y 轴缩小 1/3 ,变成右边紫色向量。

从上面两个实例可以看出,旋转缩放前,第一个图的原始向量要比第二个图的原始向量要短,但是做了同样的旋转缩放后,第一个图的结果向量反而比第二个图的结果向量要长,可见,旋转缩放后,会改变向量长度的大小关系,进而影响 Zero Forcing 算法达不到 Maximum Likelihood 算法的效果,即可能找到的不是最优解。
另一个直观的解释就是,接收端的噪声往往是各向同性的高斯噪声,经过 H − 1 W H^{-1}W H−1W 之后的噪声会变成各向异性的噪声,从而降低了系统性能。