目录

 

前言：

简言之BN、LN、IN、GN等归一化的区别：

批量归一化(Batch Normalization，BN)

优点

缺点

计算过程

层归一化(Layer Normalization，LN)

优点 

计算过程

总结

分析torch.nn.LayerNorm()工作原理

分析torch.var()工作原理

torch.var()函数 

参数

关键字参数

重点

---

前言：

最近在学习Vit（Vision Transformer）模型，在构建自注意力层（Attention）和前馈网络层（MLP）时，用到了torch.nn.LayerNorm(dim)，也就是LN归一化，与常见卷积神经网络（CNN）所使用的BN归一化略有不同。

简言之BN、LN、IN、GN等归一化的区别：

假设输入样本为4张大小为240x240的彩色图片，因此样本Batch数量N为4，RGB彩色通道Channel为3，长H为240，宽W为240，样本数据矩阵为[4，3，240，240]

BN归一化相当于作用在通道维度上，一共3次归一化，分别求通道1、2、3的4张240x240照片的均值和方差，也就是分别计算3次[4，240，240]数据的均值和方差。

LN归一化相当于作用在样本数量上，一共4次归一化，分别求照片1、2、3、4的均值和方差，也就是计算4次[3，240，240]数据的均值和方差。

IN归一化相当于作用在样本数量和通道维度上，一共3x4=12次归一化，分别求照片1、2、3、4的通道1、2、3的均值和方差，也就是计算12次[240，240]数据的均值和方差。

GN归一化相当于作用在样本数量和以组为单位的通道维度上，例如将通道维度分为两组，第一组为通道1、2，第二组为通道3，一共2x4=8次归一化，分别求照片1、2、3、4的通道组1的均值和方差和照片1、2、3、4的通道组2的均值和方差，也就是计算4次[2，240，240]和4次[1，240，240]数据的均值和方差。

批量归一化(Batch Normalization，BN)

优点

1、极大提升了训练速度，收敛过程大大加快；

2、减弱对初始化的强依赖性；

3、保持隐藏层中数值的均值、方差不变，让数值更稳定，为后面网络提供坚实的基础；

4、还能增加分类效果，一种解释是这是一种防止过拟合的正则化表达方式（相当于给隐藏层加入噪声，类似Dropout），所以不用Dropout也能达到相当的效果；

5、另外调参过程也简单多了，对于初始化要求没那么高，而且可以使用大的学习率等；

缺点

1、每次是在一个batch上计算均值、方差，如果batch size太小，则计算的均值、方差不足以代表整个数据分布。

2、batch size太大会超过内存容量；需要跑更多的epoch，导致总训练时间变长；会直接固定梯度下降的方向，导致很难更新。

由于BN与mini-batch的数据分布紧密相关，故而mini-batch的数据分布需要与总体的数据分布近似相等。因此BN适用于batch size较大且各mini-batch分布相近似的场景下（训练前需进行充分的shuffle）。BN计算过程需要保存某一层神经网络batch的均值和方差等统计信息，适合定长网络结构DNN CNN，不适用动态网络结构RNN。

计算过程

1、沿着通道计算每个batch的均值μ

2、沿着通道计算每个batch的方差σ²

3、将每个值进行归一化（分母方差加了一个极小数，防止分母为0）

4、加入缩放和平移变量 γ 和 β（深度学习就是在学习变量 γ 和 β的大小）

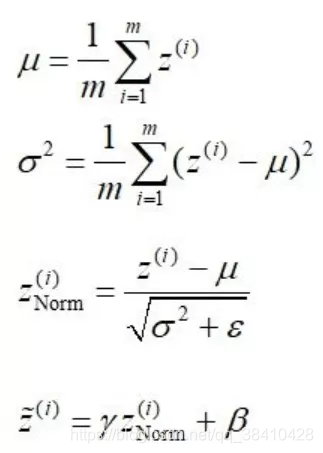
详细内容补充：

笔记详情 (bilibili.com)

层归一化(Layer Normalization，LN)

优点 

LN不受batch size的影响。同时，LN可以很好地用到序列型网络RNN中。 

计算过程

针对BN不适用于深度不固定的网络（sequence长度不一致，如RNN），LN对深度网络的某一层的所有神经元的输入按以下公式进行normalization操作。

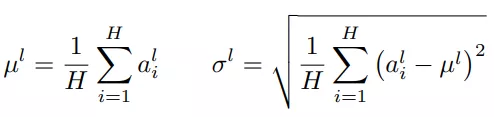
LN中同层神经元的输入拥有相同的均值和方差，不同的输入样本有不同的均值和方差。
对于特征图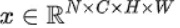 ，LN 对每个样本的 C、H、W 维度上的数据求均值和标准差，保留 N 维度。其均值和标准差公式为：

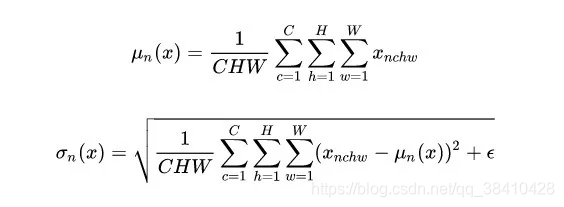
Layer Normalization (LN) 的一个优势是不需要批训练，在单条数据内部就能归一化。LN不依赖于batch size和输入sequence的长度，因此可以用于batch size为1和RNN中。LN用于RNN效果比较明显，但是在CNN上，效果不如BN。

总结

我们将feature map shape 记为[N, C, H, W]。如果把特征图比喻成一摞书，这摞书总共有 N 本，每本有 C 页，每页有 H 行，每行 有W 个字符。

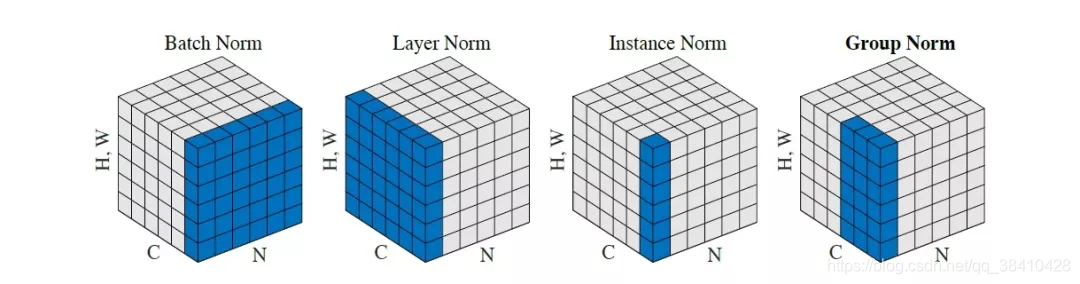
1、BN是在batch上，对N、H、W做归一化，而保留通道 C 的维度。BN 相当于把这些书按页码一一对应地加起来，再除以每个页码下的字符总数：N×H×W。

2、LN在通道方向上，对C、H、W归一化。LN 相当于把每一本书的所有字加起来，再除以这本书的字符总数：C×H×W。

3、IN在图像像素上，对H、W做归一化。IN 相当于把一页书中所有字加起来，再除以该页的总字数：H×W。

4、GN将channel分组，然后再做归一化。GN 相当于把一本 C 页的书平均分成 G 份，每份成为有 C/G 页的小册子，对每个小册子做Norm。

另外，还需要注意它们的映射参数γ和β的区别：对于 BN，IN，GN， 其γ和β都是维度等于通道数 C 的向量。而对于 LN，其γ和β都是维度等于 normalized_shape 的矩阵。

最后，BN 和 IN 可以设置参数：momentum和track_running_stats来获得在整体数据上更准确的均值和标准差。LN 和 GN 只能计算当前 batch 内数据的真实均值和标准差。

IN和GN请参考 ：

(14条消息) 常用的归一化（Normalization） 方法：BN、LN、IN、GN_归一化方法_初识-CV的博客-CSDN博客

深度学习之9——逐层归一化(BN，LN) - 知乎 (zhihu.com)

其他归一化方法可见博主另一篇文章：

(14条消息) 【机器学习】数据归一化全方法总结：Max-Min归一化、Z-score归一化、数据类型归一化、标准差归一化等_daphne odera�的博客-CSDN博客

分析torch.nn.LayerNorm()工作原理

通过以下代码分析torch.nn.LayerNorm()在nlp模型中是如何工作的，计算输入数据是一批单词嵌入序列： 

import torch

batch_size, seq_size, dim = 1, 2, 3
embedding = torch.randn(batch_size, seq_size, dim)
print("x: ", embedding)

layer_norm = torch.nn.LayerNorm(dim)
print("y: ", layer_norm(embedding))

 结果如下：

x:  tensor([[[-0.5975,  2.0992,  0.1889],
         [ 0.9362,  1.2452, -0.7753]]])
y:  tensor([[[-1.0253,  1.3562, -0.3309],
         [ 0.5261,  0.8738, -1.3999]]], grad_fn=<NativeLayerNormBackward0>)

我们编写LN归一化的代码，模拟torch.nn.LayerNorm()工作流程：

def custom_layer_norm(
    x: torch.Tensor, dim: tuple[int] = -1, eps: float = 0.00001
) -> torch.Tensor:
    mean = torch.mean(embedding, dim=dim, keepdim=True)
    var = torch.square(embedding - mean).mean(dim=(-1), keepdim=True)
    return (embedding - mean) / torch.sqrt(var + eps)

print("y_custom: ", custom_layer_norm(embedding))

 结果如下（一模一样）：

y_custom:  tensor([[[-1.0253,  1.3562, -0.3309],
         [ 0.5261,  0.8738, -1.3999]]])

未加入上述所说的缩放和平移变量 γ 和 β，直接通过每个样本嵌入值的均值和方差来计算：

mean = torch.mean(embedding[0, :, :])
std = torch.sqrt(torch.var(embedding[0, :, :], unbiased=False)) # 母体方差 分母为N unbiased默认为True 样本方差 无偏估计 分母为n-1
print("mean: ", mean)
print("std: ", std)
print((embedding[0, 0, :] - mean) / std)

结果如下（较为接近）：

mean:  tensor(0.5161)
std:  tensor(1.0189)
tensor([-1.0929,  1.5537, -0.3212])

分析torch.var()工作原理

在计算方差时，使用了torch.var()函数，仅由一个参数决定torch.var()计算的是样本方差还是母体方差，所以着重讲解一下。

import numpy as np
print("np.var: ", np.var([[1, 2], [2, 3]]))

# 结果如下

np.var:  0.5

我们在写一个案例：

X_test = torch.tensor([[1, 2], [2, 3]], dtype=torch.float32)
print("np.var unbiased=Ture: ", torch.var(X_test))
print("np.var unbiased=False: ", torch.var(X_test, unbiased=False))

# 结果如下

np.var unbiased=True:  tensor(0.6667)
np.var unbiased=False:  tensor(0.5000)

为什么结果不一样呢，因为取决于一个参数，即unbiased，无偏的意思。默认值为true，也就是说，默认是计算样本方差，当unbiased=False时，计算的是母体方差，也就是无偏估计。

torch.var()函数 

torch.var(input, dim, unbiased, keepdim=False, *, out=None) → Tensor

参数

• input(Tensor) -输入张量。

• dim(int或者python的元组：ints) -要减小的尺寸或尺寸。

关键字参数

• unbiased(bool) -是否使用贝塞尔校正(δN=1)。

• keepdim(bool) -输出张量是否保留了dim。

• out(Tensor,可选的) -输出张量。

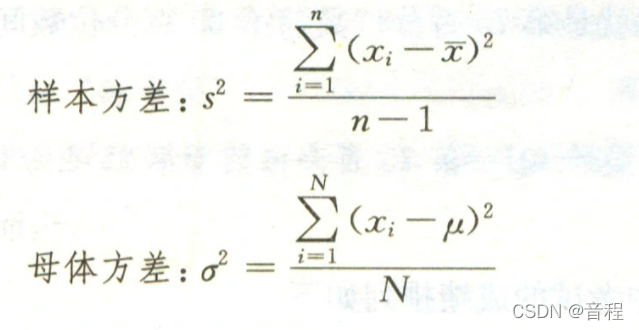
重点

 当unbiased=True时（默认），计算的是样本方差，分母是样本数量-1

 当unbiased=False时，计算的是母体方差，也就是无偏估计，分母是样本数量