AI自动寻路AStar算法【图示讲解原理】

news2025/1/16 6:48:28

文章目录

  • AI自动寻路AStar算法
    • 背景
    • AStar算法原理
    • AStar寻路步骤
    • AStar具体寻路过程
    • AStar代码实现
    • 运行结果

AI自动寻路AStar算法

背景

AI自动寻路的算法可以分为以下几种：

1、A*算法：A*算法是一种启发式搜索算法，它利用启发函数（heuristic function）来评估节点的估价函数（estimated cost function），从而寻找最短路径。A*算法综合考虑了节点的实际代价和到目标节点的预计代价，因此能够快速而准确地寻找最短路径【不一定最短，A*算法并不一定能够找到最短路径，但它通常可以找到接近最短路径的解决方案。】

2、Dijkstra算法：Dijkstra算法是一种贪心算法，它从起点开始，每次选择当前代价最小的节点作为下一个节点。通过不断更新节点的代价，最终可以找到起点到终点的最短路径。

3、Bellman-Ford算法：Bellman-Ford算法是一种动态规划算法，它通过不断更新节点的代价，直到收敛到最短路径。相比于Dijkstra算法，Bellman-Ford算法能够处理负权边的情况。

4、Floyd-Warshall算法：Floyd-Warshall算法是一种动态规划算法，它能够计算出图中任意两点之间的最短路径。Floyd-Warshall算法通过不断更新节点之间的代价，直到收敛到最短路径。

这些算法都可以用于AI自动寻路，具体选择哪种算法需要根据具体的应用场景和性能要求进行选择。

随着 3D 游戏的日趋流行,在复杂的 3D 游戏环境中如何能使非玩家控制角色准确实现自动寻路功能成为了 3D 游戏开
发技术中一大研究热点。其中 A*算法得到了大量的运用，A*算法较之传统的路径规划算法,实时性更高、灵活性更强,寻路
结果更加接近人工选择的路径结果. A*寻路算法并不是找到最优路径，只是找到相对近的路径，因为找最优要把所有可行
路径都找出来进行对比，消耗性能太大，寻路效果只要相对近路径就行了。
所以对于自动寻路，A*算法是一个很不错的选择！！！
在这里插入图片描述

AStar算法原理

我们假设在推箱子游戏中人要从站里的地方移动到右侧的箱子目的地，但是这两点之间被一堵墙隔开。
在这里插入图片描述

我们下一步要做的便是查找最短路径。既然是 AI 算法， A* 算法和人寻找路径的做法十分类似，当我们离目标较远时，我
们的目标方向是朝向目的点直线移动，但是在近距离上因为各种障碍需要绕行（走弯路）！而且已走过的地方就无须再次
尝试。
为了简化问题，我们把要搜寻的区域划分成了正方形的格子。这是寻路的第一步，简化搜索区域，就像推箱子游戏一样。
这样就把我们的搜索区域简化为了 2 维数组。数组的每一项代表一个格子，它的状态就是可走 (walkalbe) 和不可走
(unwalkable) 。通过计算出从起点到终点需要走过哪些方格，就找到了路径。一旦路径找到了，人物便从一个方格的中心
移动到另一个方格的中心，直至到达目的地。

简化搜索区域以后，如何定义小人当前走要走的格子离终点是近是远呢？我们需要两个指标来表示：
1、 G 表示从起点移动到网格上指定方格的移动距离 (暂时不考虑沿斜向移动，只考虑上下左右移动)。
2、 H 表示从指定的方格移动到终点的预计移动距离，只计算直线距离 (H 有很多计算方法, 这里我们设定只可以上
下左右移动，即该点与终点的直线距离)。
在这里插入图片描述
令 F = G + H ，F 即表示从起点经过此点预计到终点的总移动距离

AStar寻路步骤

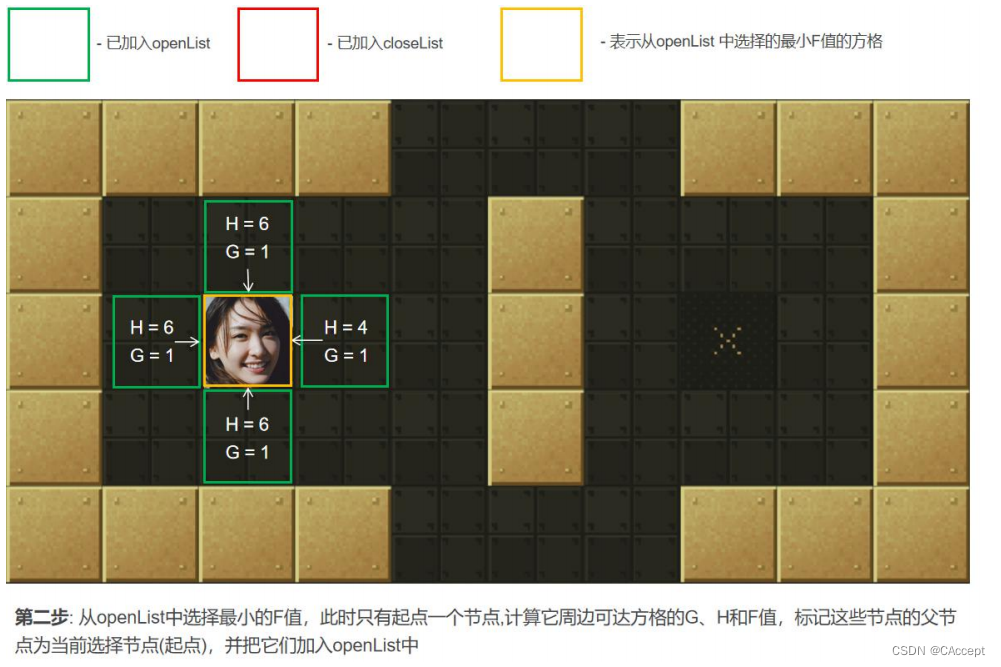
1、从起点开始, 把它作为待处理的方格存入一个预测可达的节点列表，简称 openList, 即把起点放入“预测可达节点列表”，可达节点列表 openList 就是一个等待检查方格的列表。

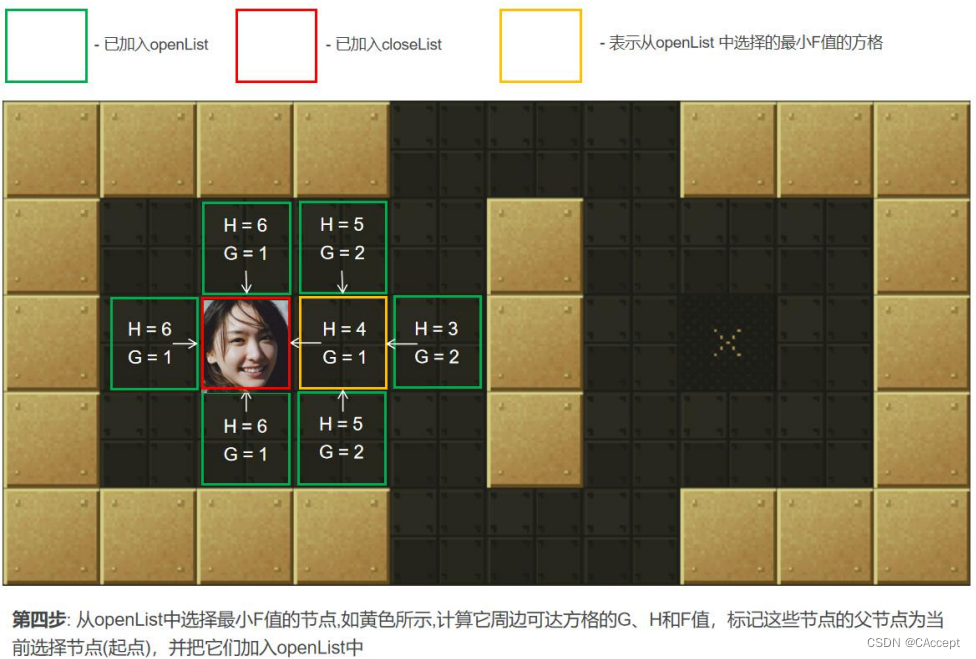
2、寻找 openList 中 F 值最小的点 min（一开始只有起点）周围可以到达的方格（可到达的意思是其不是障碍物，也不存在关闭列表中的方格,即不是已走过的方格）。计算 min 周围可到达的方格的 F 值。将还没在 openList 中点放入其中, 并设置它们的"父方格"为点 min,表示他们的上一步是经过 min 到达的。如果 min 下一步某个可到达的方格已经在 openList列表那么并且经 min 点它的 F 值更优,则修改 F 值并把其"父方格"设为点 min。

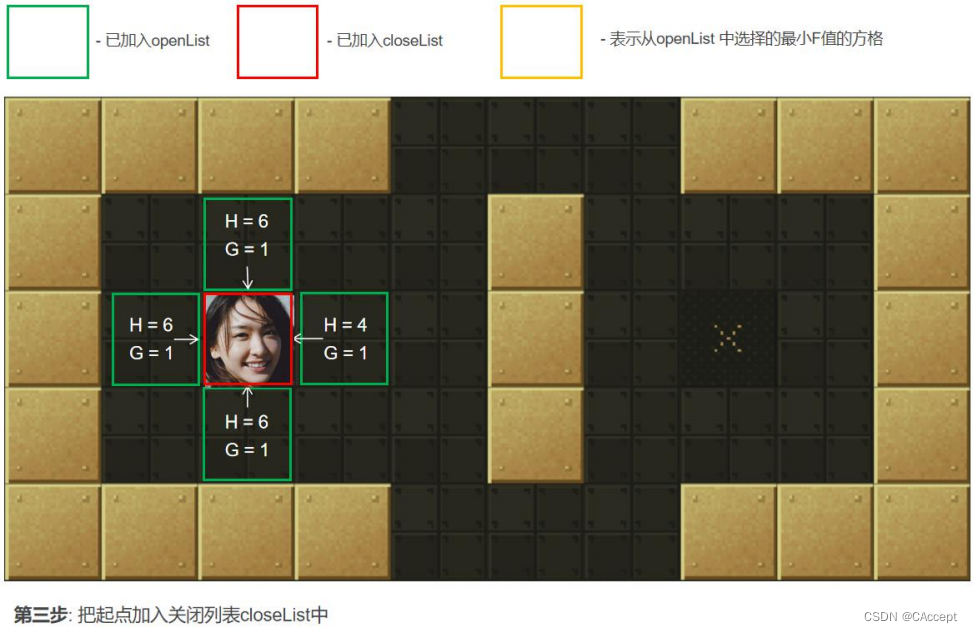
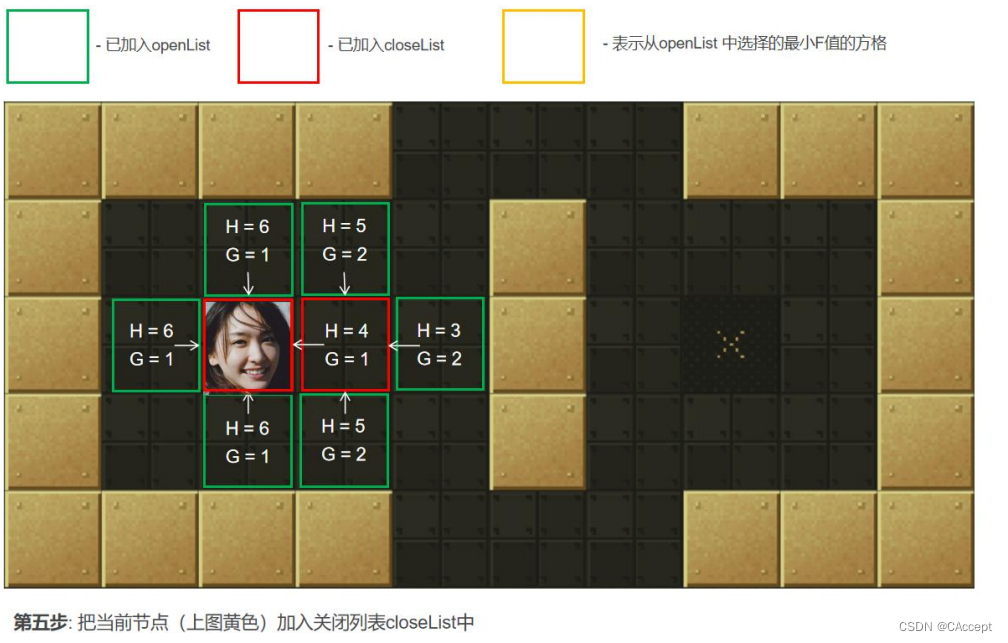
3、把 2 中的点 min 从"开启列表"中删除并存入"关闭列表"closeList 中【当自己对四周扩散时，将自己放入到closeList中】, closeList 中存放的都是不需要再次检查的方格。如果 2 中点 min 不是终点并且开启列表的数量大于零，那么继续从第 2 步开始。如果是终点执行第 4 步，如果 openList 列表数量为零，那么就是找不到有效路径。

4、如果第 3 步中 min 是终点，则结束查找，直接追溯父节点到起点的路径即为所选路径。

AStar具体寻路过程

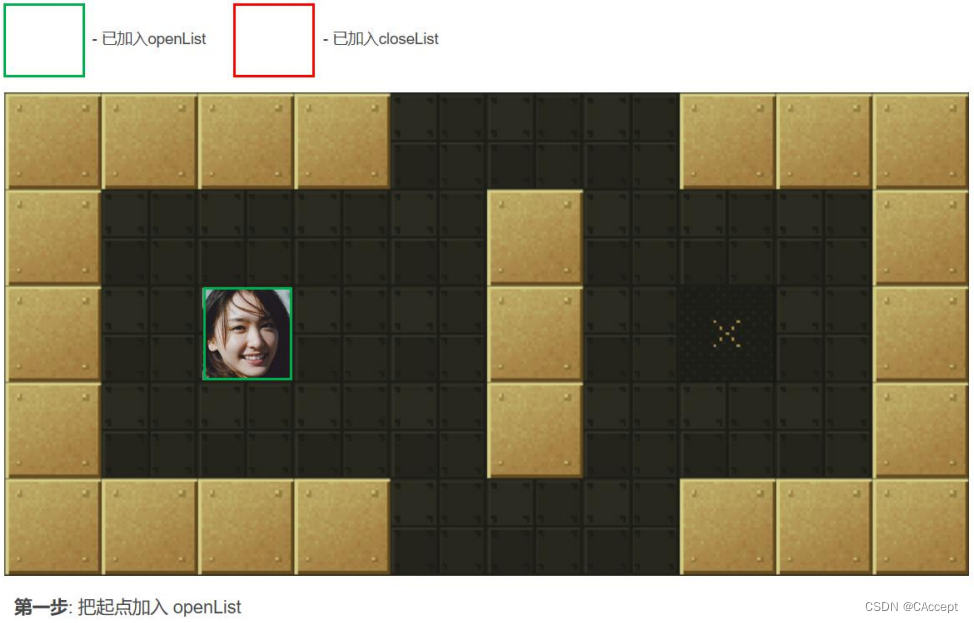
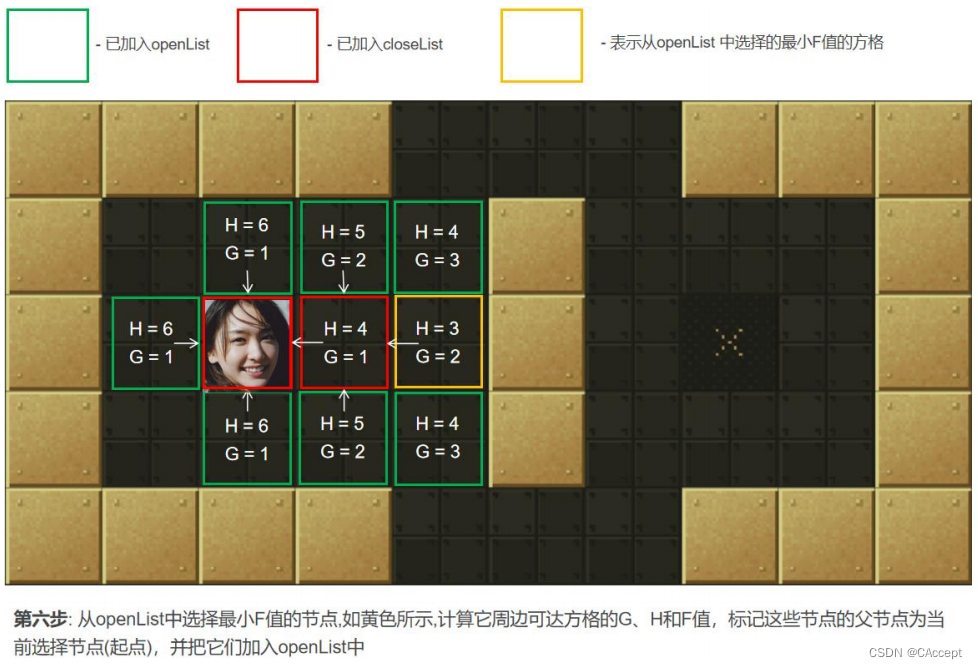
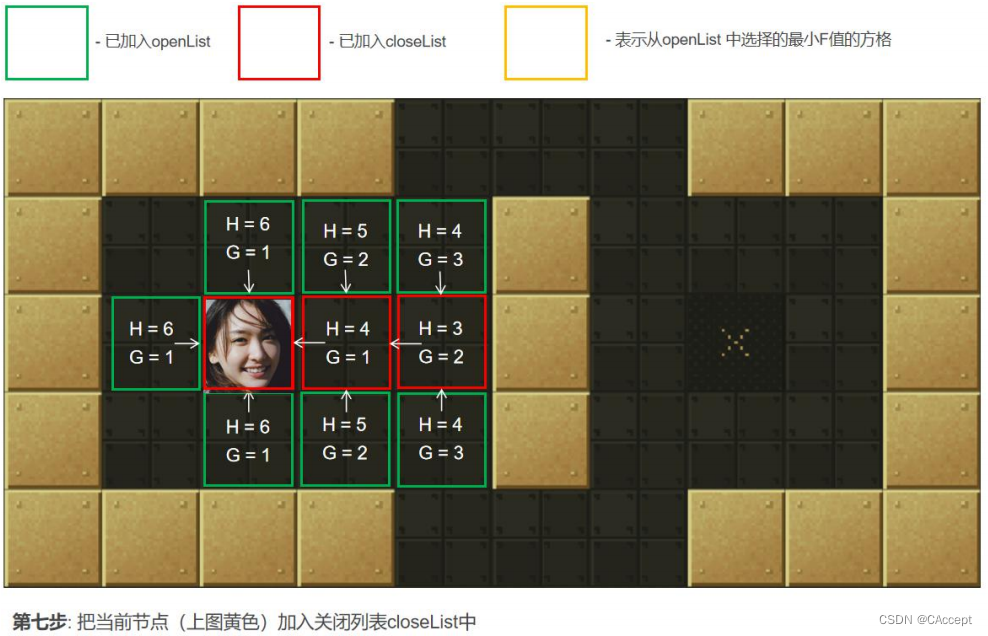
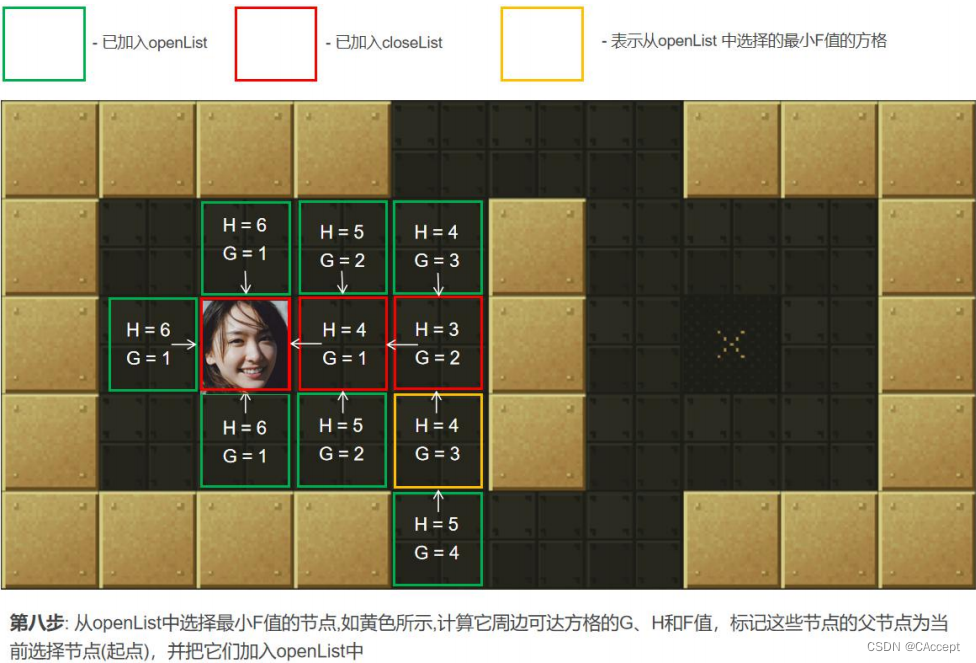
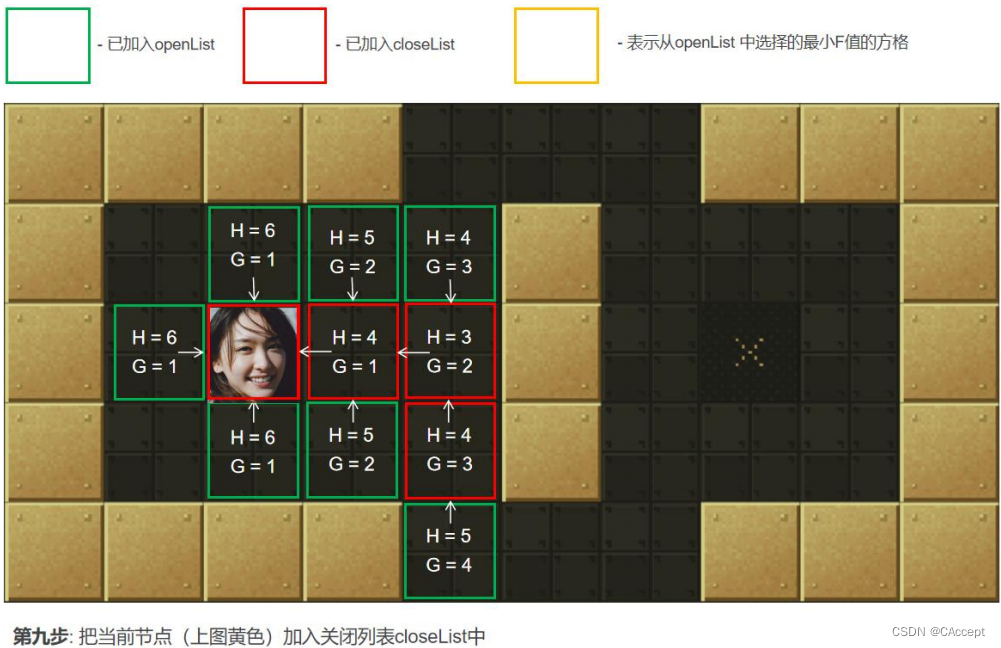
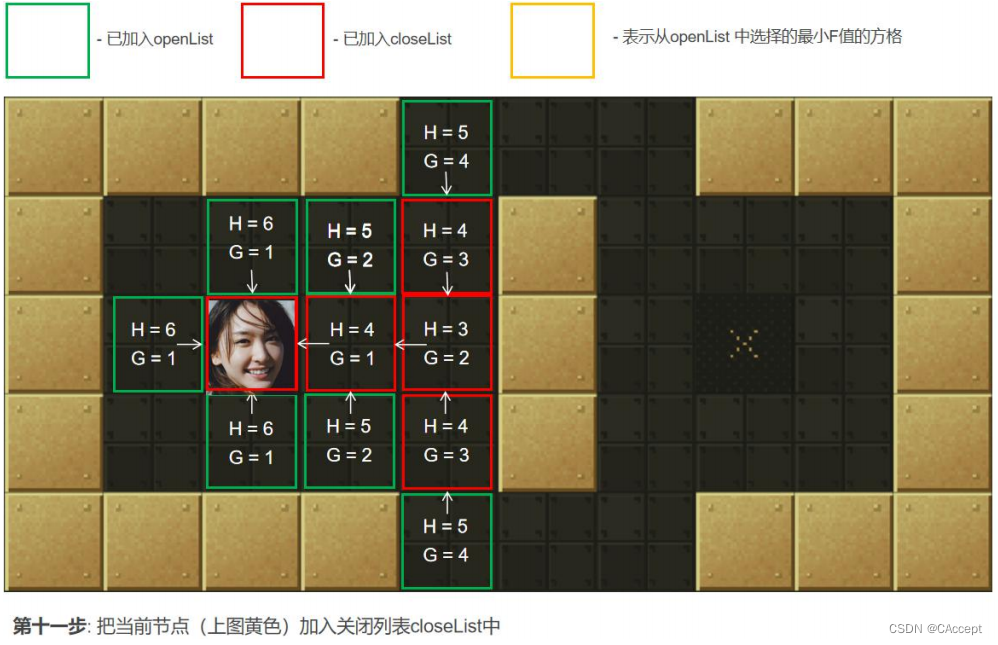
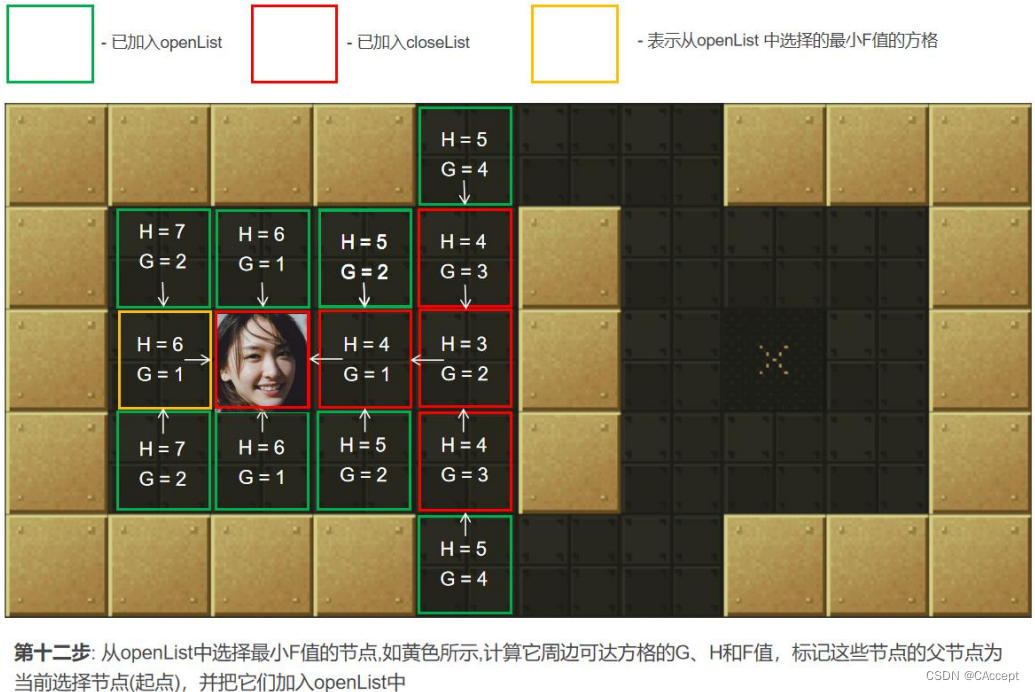
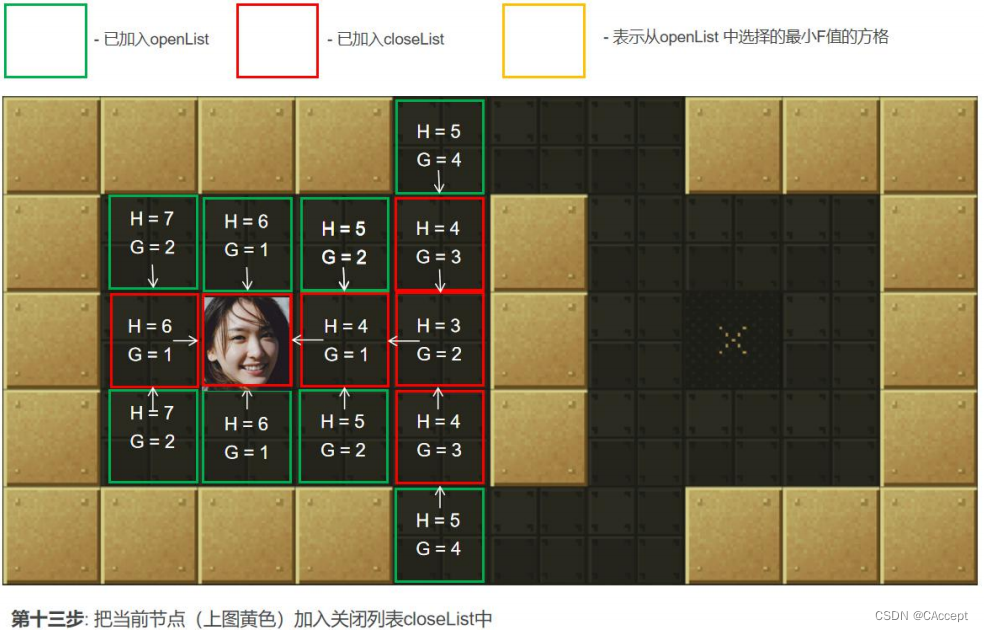
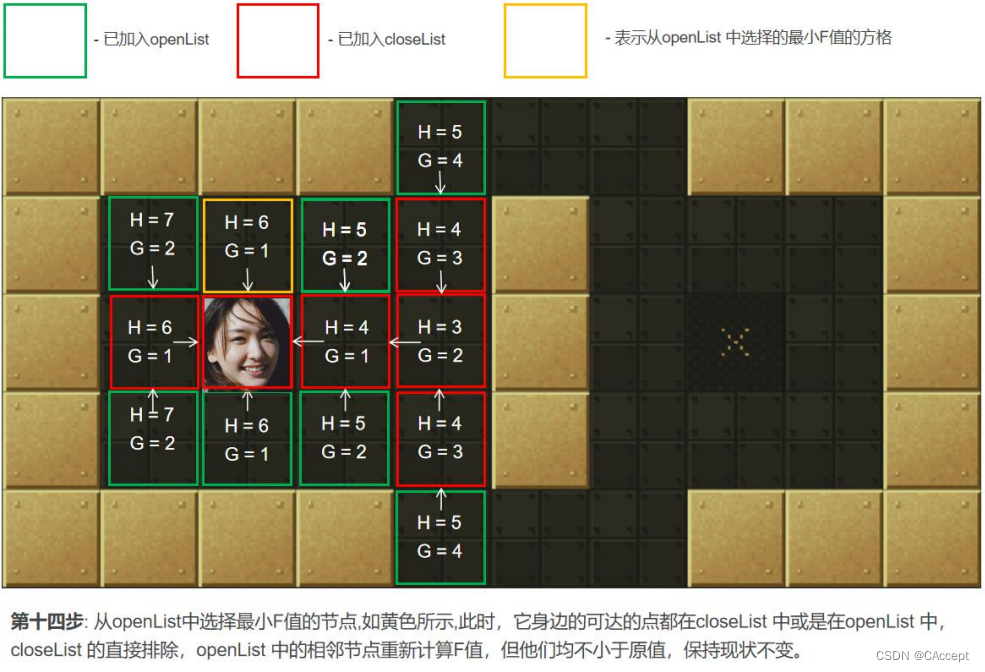
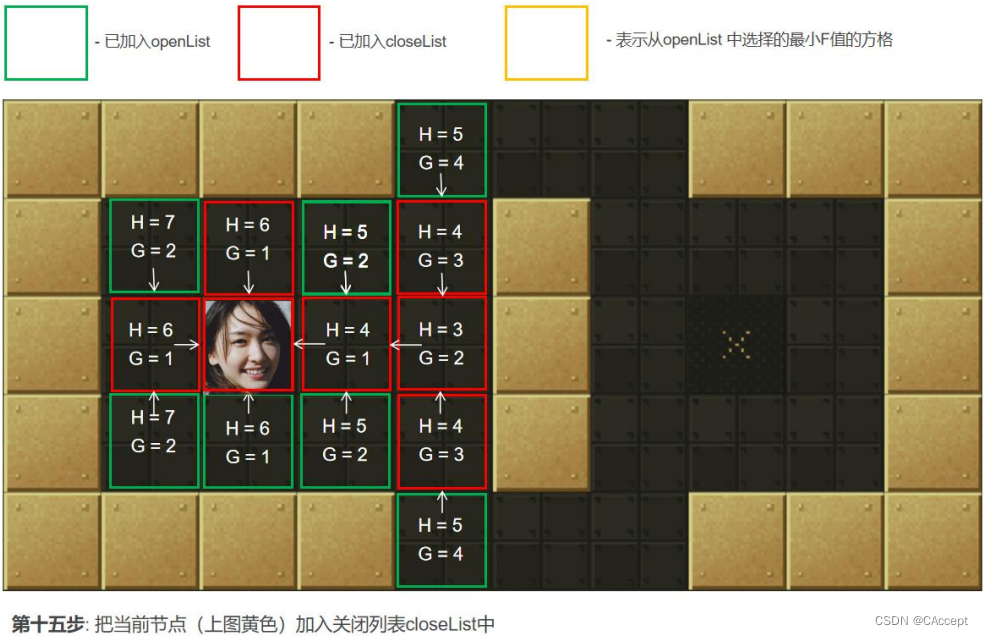
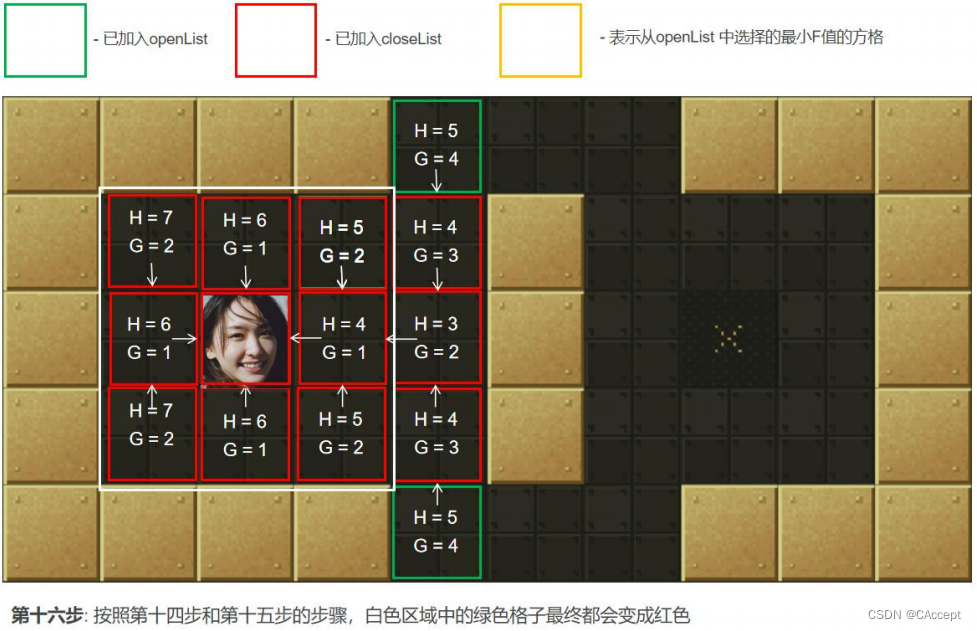
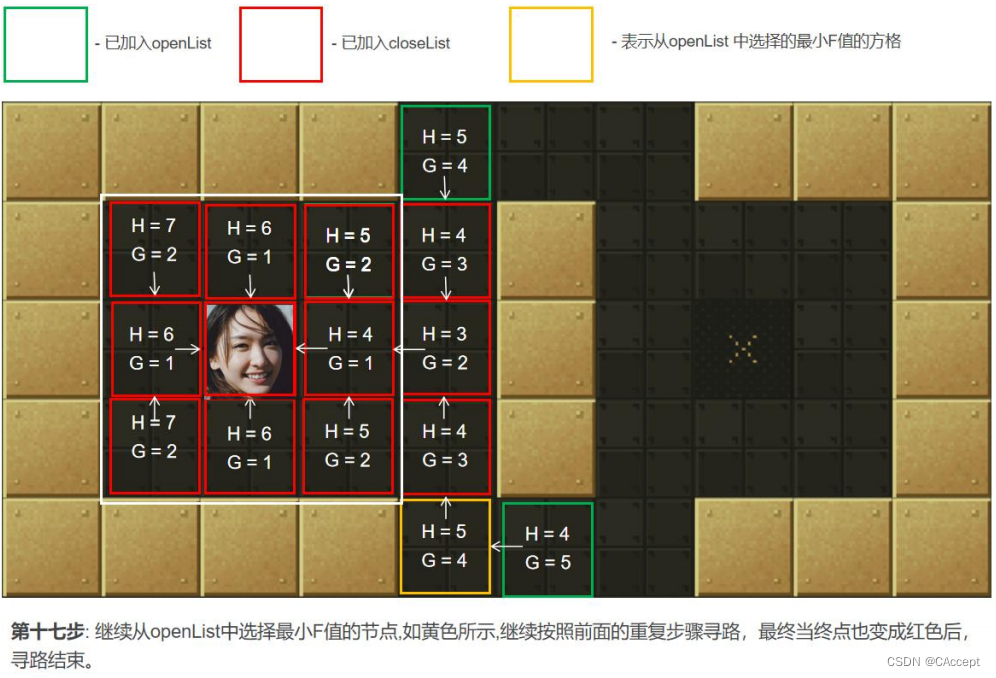
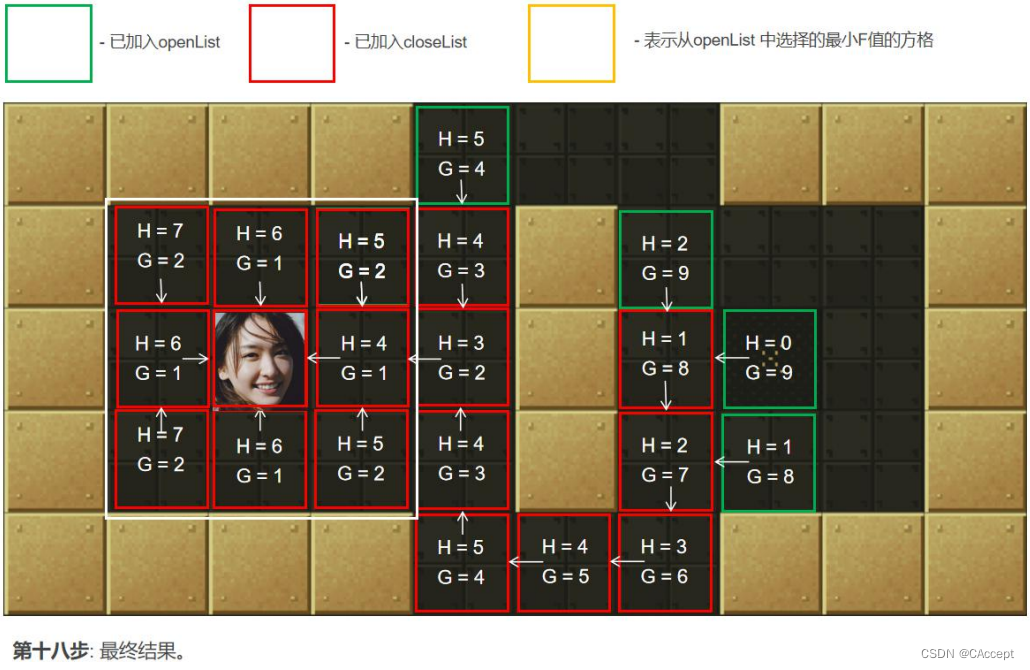
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述
最后通过父子关系将一条起点到终点的路径完整的描述出来

AStar代码实现

Astar.h

#pragma once
#include<list>//链表
#include<vector>
const int k_Cost1 = 10;//走一格消耗10
const int k_Cost2 = 14;//斜移走一个消耗14

typedef struct _Point {
	int x, y;  //x为行，y为列
	int F, G, H;  //F=G+H;
	struct _Point* parent;  //父节点的坐标
}Point;

//分配一个节点
Point* AllocPoint(int x, int y);


//初始化地图，地图，行，列
void InitAstarMaze(int* _maze, int _line, int _colums);

//通过A*算法寻找路径
std::list<Point*>GetPath(const Point* startPoint, const Point* endPoint);


//查找路径的小方法,返回一个终点，根据终点可以回溯到起点
static Point* findPath(const Point* startPoint, const Point* endPoint);//用static是为了只能在函数内部调用而不能单独的使用

//返回开放列表中F的最小值的点
static Point* getLeastFPoint();

//获取周围的节点
static std::vector<Point*> getSurroundPoint(const Point* point);

//某个点是否可达
static bool isCanreach(const Point* point, const Point* target);

//是否存在某个list中，这里用作是否存在closeList/openList中
static Point* isInList(const std::list<Point*>& list, const Point* point);

//获取G，H，F
static int caloG(const Point* temp_start, const Point* point);
static int caloH(const Point* point, const Point* end);
static int caloF(const Point* point);

//清理资源
void clearAstarMaze();

Astar.cpp

#include"Astar.h"
#include<cmath>
#include<iostream>
#include<vector>
//extern int k_Cost1;
//extern int k_Cost2;

static int* maze;//初始化迷宫
static int cols;//二维数组对应的列
static int lines;//二维数组对应的行

static std::list<Point*>openList;  //开放列表
static std::list<Point*>closeList; //关闭列表


/*初始化地图*/
void InitAstarMaze(int* _maze, int _line, int colums) {//一级指针保存二维数组
	maze = _maze;
	lines = _line;
	cols = colums;
}

/*分配节点*/
Point* AllocPoint(int x, int y) {
	Point* temp = new Point;
	memset(temp, 0, sizeof(Point));//清理养成好习惯

	temp->x = x;
	temp->y = y;
	return temp;
}

/*通过A*算法寻找路径*/
std::list<Point*>GetPath(const Point* startPoint, const Point* endPoint) {
	Point *result = findPath(startPoint, endPoint);
	std::list<Point*>path;

	//返回路径
	while (result) {
		path.push_front(result);//这样起点就是在这个链表的最前面了
		result = result->parent;
	}

	return path;

}

/*查找路径的小方法,返回一个终点，根据终点可以回溯到起点*/
static Point* findPath(const Point* startPoint, const Point* endPoint) {
	openList.push_back(AllocPoint(startPoint->x, startPoint->y));//重新分配更加的安全，置入起点

	while (!openList.empty()) {
		//1、获取开放表中最小的F值
		Point* curPoint = getLeastFPoint();

		//2、把当前节点放到closeList中
		openList.remove(curPoint);
		closeList.push_back(curPoint);

		//3、找到当前节点周围可到达的节点并计算F值
		std::vector<Point*> surroundPoints = getSurroundPoint(curPoint);

		std::vector<Point*>::const_iterator iter;
		for (iter = surroundPoints.begin(); iter != surroundPoints.end(); iter++) {
			Point* target = *iter;

			//如果没在开放列表中就加入到开放列表，设置当前节点为父节点
			Point* exist = isInList(openList, target);
			if (!exist) {

				target->parent = curPoint;
				target->G = caloG(curPoint, target);//父节点的G加上某个数就好（自己设计的）
				target->H = caloH(target, endPoint);
				target->F = caloF(target);

				openList.push_back(target);
			}
			else {//如果已存在就重新计算G值看要不要替代
				int tempG = caloG(curPoint, target);
				if (tempG < target->G) {//更新
					exist->parent = curPoint;
					exist->G = tempG;
					exist->F = caloF(target);
				}

				delete *iter;
			}

		}//end for循环

		surroundPoints.clear();
		Point* resPoint = isInList(openList, endPoint);//终点是否在openList上
		if (resPoint) {
			return resPoint;
		}


	}


	return NULL;
}

//返回开放列表中F的最小值的点
static Point* getLeastFPoint() {
	//遍历
	if (!openList.empty()) {
		Point* resPoint = openList.front();

		std::list<Point*>::const_iterator itor;//定义迭代器，用于遍历链表

		//迭代器遍历，C++特性,直接理解成平时我们用的for
		for (itor = openList.begin(); itor != openList.end(); itor++) {
			Point* p = *itor;//把元素拿出来
			if (p->F < resPoint->F) {
				resPoint = p;
			}
		}
		return resPoint;
	}
	return NULL;
}

/*获取周围的节点*/
static std::vector<Point*> getSurroundPoint(const Point* point) {
	std::vector<Point*>surroundPoints;
	//周围九个点都会进行检测
	for (int x = point->x - 1; x <= point->x + 1; x++) {
		for (int y = point->y - 1; y <= point->y + 1; y++) {
			Point* temp = AllocPoint(x, y);
			if (isCanreach(point, temp)) {
				surroundPoints.push_back(temp);
			}
			else {
				delete temp;
			}
		}
	}
	return surroundPoints;
}


/*某个点是否可达*/
static bool isCanreach(const Point* point, const Point* target) {
	if (target->x<0 || target->x>(lines - 1)
		|| target->y<0 || target->y>(cols - 1)
		|| (maze[target->x * cols + target->y] == 1)//找到对应的二维数组中的位置-》障碍物
		|| (maze[target->x * cols + target->y] == 2)
		|| (target->x == point->x && target->y == point->y)
		|| isInList(closeList, target)) {
		return false;

	}

	if (abs(point->x - target->x) + abs(point->y - target->y) == 1) {//我们现在只考虑上下左右4个点
		return true;
	}
	else {
		return false;
	}
}


/*是否存在某个list中，这里用作是否存在closeList/openList中*/
static Point* isInList(const std::list<Point*>& list, const Point* point) {
	std::list<Point*>::const_iterator itor;
	for (itor = list.begin(); itor != list.end(); itor++) {
		if ((*itor)->x == point->x && (*itor)->y == point->y) {
			return *itor;  //存在返回该节点
		}
	}
	return NULL;
}

static int caloG(const Point* temp_start, const Point* point) {
	int extraG = (abs(point->x - temp_start->x) + abs(point->y - temp_start->y)) == 1 ? k_Cost1 : k_Cost2;//周围的点与扩散点的差值,是否为斜边
	int parentG = (point->parent == NULL ? NULL : point->parent->G);//如果是初始值为null，其他的点是父类的G值
	return parentG + extraG;//返回两个量相加
}

static int caloH(const Point* point, const Point* end) {
	//欧几里得求斜边
	return (int)sqrt((double)(end->x - point->x) * (double)(end->x - point->x)) + (double)(end->y - point->y) * (double)(end->y - point->y) * k_Cost1;

}

static int caloF(const Point* point) {
	return point->G + point->H;
}

/*清理资源*/
void clearAstarMaze() {
	maze = NULL;
	lines = 0;
	cols = 0;
	std::list<Point*>::iterator itor;
	for (itor = openList.begin(); itor != openList.end();) {
		delete* itor;
		itor = openList.erase(itor);//获取到下一个节点
	}
	for (itor = closeList.begin(); itor != closeList.end();) {
		delete* itor;
		itor = closeList.erase(itor);//获取到下一个节点
	}
}

main.cpp

#include<iostream>
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <windows.h>
#include"Astar.h"
using namespace std;
int map[13][13] = {
{0,0,0,0,0,0,0,0,0,0,0,0,0},
{0,1,0,1,0,1,0,1,0,1,0,1,0},
{0,1,0,1,0,1,0,1,0,1,0,1,0},
{0,1,0,1,0,1,2,1,0,1,0,1,0},
{0,1,0,1,0,1,0,1,0,1,0,1,0},
{0,1,0,1,0,0,0,1,0,1,0,1,0},
{0,0,0,0,0,1,0,1,0,0,0,0,0},
{2,0,1,1,0,0,0,1,0,1,0,0,2},
{0,0,0,0,0,1,1,1,0,0,0,0,0},
{0,1,0,1,0,1,0,1,0,1,0,1,0},
{0,1,0,1,0,1,0,1,0,1,0,1,0},
{0,1,0,1,0,0,0,0,0,1,0,1,0},
{0,0,0,0,0,1,3,1,0,0,0,0,0}
};
void astarTest() {

	InitAstarMaze(&map[0][0], 13, 13);
	//设置
	Point* start = AllocPoint(12, 4);
	Point* end = AllocPoint(0, 12);

	//寻找路径
	list<Point*>path = GetPath(start, end);

	//设置迭代器遍历
	list<Point*>::const_iterator iter;//迭代器

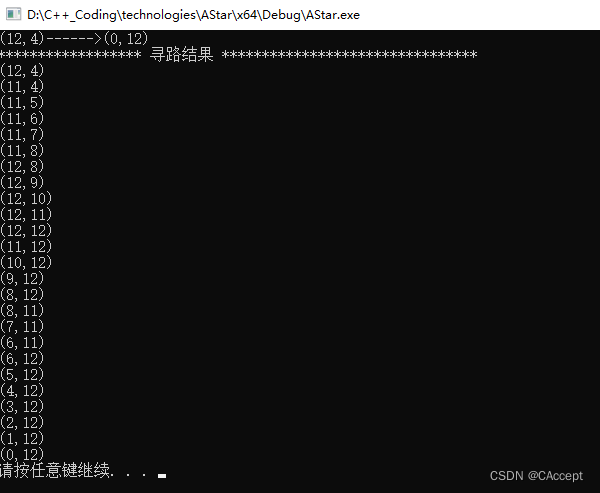
	cout << "(" << start->x << "," << start->y << ")" << "------>(" << end->x << "," << end->y << ")" << endl;
	cout << "****************** 寻路结果 ********************************" << endl;
	for (iter = path.begin(); iter != path.end(); ) {
		Point* cur = *iter;
		cout << '(' << cur->x << "," << cur->y << ')' << endl;
		//delete cur;//不用再进行释放了因为在openList和closeList链表中我们最后都有清理，如果再清理就会报错
		iter = path.erase(iter);
		Sleep(800);  //休眠
	}
	clearAstarMaze();
}
int main() {
	astarTest();
	system("pause");
	return 0;
}

运行结果

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/415696.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Jmeter接口测试和性能测试

Jmeter接口测试和性能测试

目前最新版本发展到5.0版本&#xff0c;需要Java7以上版本环境&#xff0c;下载解压目录后&#xff0c;进入\apache-jmeter-5.0\bin\&#xff0c;双击ApacheJMeter.jar文件启动JMemter。 1、创建测试任务 添加线程组&#xff0c;右击测试计划&#xff0c;在快捷菜单单击添加-…
阅读更多...
STM32F103RCT6驱动SG90舵机-完成正反转角度控制

STM32F103RCT6驱动SG90舵机-完成正反转角度控制

一、SG90舵机介绍 SG90是一种微型舵机&#xff0c;也被称为伺服电机。它是一种小型、低成本的直流电机&#xff0c;通常用于模型和机器人控制等应用中。SG90舵机可以通过电子信号来控制其精确的位置和速度。它具有体积小、重量轻、响应快等特点&#xff0c;因此在各种小型机械…
阅读更多...
亚马逊测评只能下单上好评？卖家倾向养号测评还有这些骚操作

亚马逊测评只能下单上好评？卖家倾向养号测评还有这些骚操作

亚马逊测评这对于绝大部分亚马逊卖家来说都不陌生&#xff0c;如今的亚马逊市场也很多卖家都在用测评科技来打造爆款。不过很多对于亚马逊测评的认知只停留在简单的刷销量&#xff0c;上好评。殊不知亚马逊养号测评还有其它强大的骚操作。 亚马逊自养号测评哪些功能呢&#xf…
阅读更多...
PyTorch 深度学习实战 |用 TensorFlow 训练神经网络

PyTorch 深度学习实战 |用 TensorFlow 训练神经网络

为了更好地理解神经网络如何解决现实世界中的问题&#xff0c;同时也为了熟悉 TensorFlow 的 API&#xff0c;本篇我们将会做一个有关如何训练神经网络的练习&#xff0c;并以此为例&#xff0c;训练一个类似的神经网络。我们即将看到的神经网络&#xff0c;是一个预训练好的用…
阅读更多...
【深度学习】【分布式训练】Collective通信操作及Pytorch示例

【深度学习】【分布式训练】Collective通信操作及Pytorch示例

相关博客 【深度学习】【分布式训练】Collective通信操作及Pytorch示例 【自然语言处理】【大模型】大语言模型BLOOM推理工具测试 【自然语言处理】【大模型】GLM-130B&#xff1a;一个开源双语预训练语言模型 【自然语言处理】【大模型】用于大型Transformer的8-bit矩阵乘法介…
阅读更多...
第02章_变量与运算符

第02章_变量与运算符

第02章_变量与运算符 讲师&#xff1a;尚硅谷-宋红康&#xff08;江湖人称&#xff1a;康师傅&#xff09; 官网&#xff1a;http://www.atguigu.com 本章专题与脉络 1. 关键字&#xff08;keyword&#xff09; 定义&#xff1a;被Java语言赋予了特殊含义&#xff0c;用做专门…
阅读更多...
银河麒麟服务器ky10 sp3 x86 pgadmin使用

银河麒麟服务器ky10 sp3 x86 pgadmin使用

目录 打开网页并登录 连接数据库 备份数据库 还原数据库 打开网页并登录 打开浏览器&#xff0c;输入127.0.0.1:5050&#xff0c;输入用户名和密码登录&#xff0c; 我这边设置的用户名是123456qq.com&#xff0c;密码是 123456 连接数据库 右键选择register-Server 输…
阅读更多...
Html5版飞机大战游戏中（Boss战）制作

Html5版飞机大战游戏中（Boss战）制作

内容在“60行代码&#xff0c;制作飞机大战游戏”的基础上&#xff0c;继续追加入了Boss战的功能。 boss的血量默认设置为100了&#xff0c;可以二次开发调整……(^_^) 玩起来有一定难度哈。 试玩地址&#xff1a;点击试玩 实现功能 添加玩家飞机&#xff0c;并进行控制Boss能…
阅读更多...
vue+MapboxGL：从0 到1 搭建开发环境

vue+MapboxGL：从0 到1 搭建开发环境

本系列教程是在vue2.X的基础上加载mapbox 程序，来开发各种示例程序。 安装顺序 1，下载安装nodejs 下载地址：https://nodejs.org/en/download/ 根据用户自己的机器情况进行选择不同版本的软件下载。 本教程示例采用是是windows 64位系统软件。 安装过程很简单，一路下一步…
阅读更多...
vue-router3.0处理页面滚动部分源码分析

vue-router3.0处理页面滚动部分源码分析

在使用vue-router3.0时候&#xff0c;会发现不同的路由之间来回切换&#xff0c;会滚动到上次浏览的位置&#xff0c;今天就来看看这部分的vue-router中的源码实现。 无论是基于hash还是history的路由切换&#xff0c;都对滚动进行了处理&#xff0c;这里分析其中一种即可。 无…
阅读更多...
TeeChart Pro ActiveX 2023.3.20 Crack

TeeChart Pro ActiveX 2023.3.20 Crack

TeeChart Pro ActiveX 图表组件库提供数百种 2D 和 3D 图形样式、56 种数学和统计函数供您选择&#xff0c;以及无限数量的轴和 14 个工具箱组件。图表控件可以有效地用于创建多任务仪表板。 插件的多功能性 ActiveX 图表控件作为服务器端库中的 Web 图表、脚本化 ASP 图表或桌…
阅读更多...
0201概述和结构-索引-MySQL

0201概述和结构-索引-MySQL

文章目录1 概述1.1 介绍1.2 优缺点2 索引结构2.1 BTree索引2.2 hash索引2.3 对比3 索引分类3.1 通用分类3.2 InnoDB存储引擎分类4 思考题后记1 概述 1.1 介绍 索引是帮忙MySQL 高效获取数据的数据结构&#xff08;有序&#xff09;。在数据之外&#xff0c;数据系统还维护着满…
阅读更多...
【CF1764C】Doremy‘s City Construction（二分图，贪心）

【CF1764C】Doremy‘s City Construction（二分图，贪心）

【题目描述】 有nnn个点&#xff0c;每个点的点权为aia_iai​&#xff0c;你可以在任意两个点之间连边&#xff0c;最终连成的图需要满足&#xff1a;不存在任意的三个点&#xff0c;满足au≤av≤awa_u\le a_v\le a_wau​≤av​≤aw​&#xff08;非降序&#xff09;且边(u,v)(…
阅读更多...
『pyqt5 从0基础开始项目实战』06. 获取选中多行table 重新初始化数据（保姆级图文）

『pyqt5 从0基础开始项目实战』06. 获取选中多行table 重新初始化数据（保姆级图文）

目录导包和框架代码重新初始化绑定点击事件获取当前选中的所有行id实现初始化数据完整代码main.pythreads.py总结欢迎关注 『pyqt5 从0基础开始项目实战』 专栏&#xff0c;持续更新中 欢迎关注 『pyqt5 从0基础开始项目实战』 专栏&#xff0c;持续更新中 导包和框架代码 请查…
阅读更多...
案例分享 | 金融业智能运维AIOps怎么做？看这一篇就够了

案例分享 | 金融业智能运维AIOps怎么做？看这一篇就够了

​构建双态IT系统&#xff0c;AIOps已经是必然的选择。运维数字化转型已是大势所趋&#xff0c;实体业务的逐步线上化对IT系统的稳定与安全提出更高要求&#xff0c;同时随着双态IT等复杂系统的建立&#xff0c;如何平衡IT运维效率与成本成为区域性银行面临的重要问题&#xff…
阅读更多...
Windows编程基础

Windows编程基础

Windows编程基础 Unit1应用程序分类 控制台程序&#xff1a;Console Dos程序&#xff0c;本身没有窗口&#xff0c;通过windows Dos窗口执行 窗口程序 拥有自己的窗口&#xff0c;可以与用户交互 库程序 存放代码、数据的程序&#xff0c;执行文件可以从中取出代码执行和获取…
阅读更多...
【MySQL】索引事务

【MySQL】索引事务

摄影分享~ 文章目录索引概念使用场景使用事务概念使用事务的特性索引 概念 索引是一种特殊的文件&#xff0c;包含着对数据表里所有记录的引用指针。可以对表中的一列或多列创建索引并指定索引的类型&#xff0c;各类索引有各自的数据结构实现。 通过目录&#xff0c;就可以…
阅读更多...
如何使用数字示波器

如何使用数字示波器

本文介绍以鼎阳SIGLENT SDS1122E数字示波器为例。 带了一根电源线&#xff1b;两根信号线&#xff0c;每根信号线都有几个小配件&#xff0c;如下所示&#xff1a; 使用概述 我们都知道万用表&#xff08;又称欧姆表&#xff09;是工程师最常用的调试电路的工具&#xff0c;但万…
阅读更多...
技术+商业“双轮”驱动，量旋科技加速推进全方位的量子计算解决方案

技术+商业“双轮”驱动，量旋科技加速推进全方位的量子计算解决方案

【中国&#xff0c;深圳】4月14日&#xff0c;在第三个“世界量子日”&#xff0c;以“‘双轮’驱动 加速未来”为主题的量旋科技2023战略发布会在线上举办。 本次发布会&#xff0c;量旋科技全线升级了三大业务线产品&#xff1a;其中重点布局的超导量子计算体系产品&#xf…
阅读更多...
监控系统 Prometheus 的说明

监控系统 Prometheus 的说明

一、Prometheus 是什么&#xff1f; ELK Stack 日志收集和检索平台想必大家应该比较熟悉&#xff0c;Elasticsearch Filebeat Logstash Kibana。 而 Prometheus 就相当于一整个 ELK&#xff0c;但是它其实并不是适合存储大量日志&#xff0c;也不适合长期存储&#xff08;默…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023